初中浙教版2.1 图形的轴对称说课ppt课件

这是一份初中浙教版2.1 图形的轴对称说课ppt课件，共38页。PPT课件主要包含了课堂讲解，课时流程，逐点导讲练，课堂小结，作业提升，知识点，轴对称图形，方法规律，轴对称图形的性质，问题一等内容，欢迎下载使用。

轴对称图形轴对称图形的性质轴对称轴对称的性质
北京故宫建成于1420年，整个宫殿建筑布局沿中轴 线向东西两侧展开，呈现轴对称的结构.由于轴对称给人 以美感，它被广泛应用于建筑设计上.
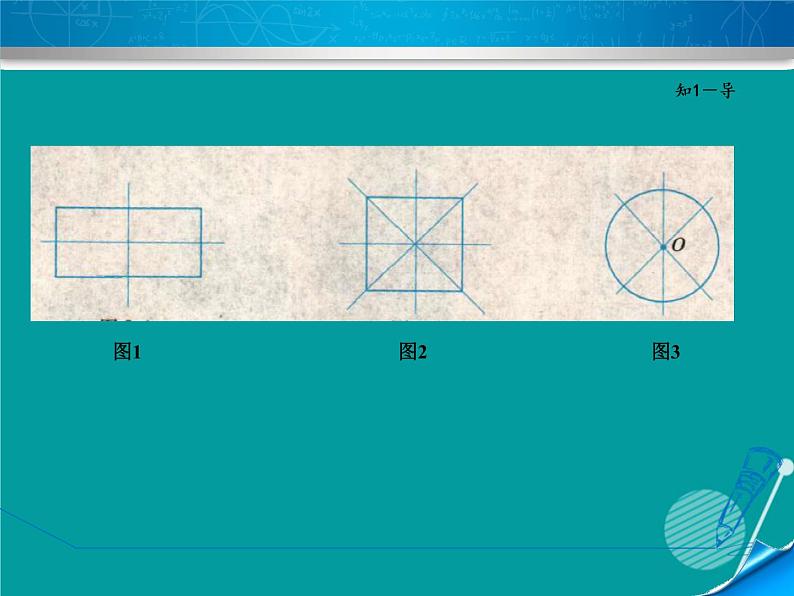
小学里我们已经学过，如果把一个图形沿着一条直线折叠后，直线两 侧的部分能够互相重合，那么这个图形叫做轴对称图形(axial symmetric figure)，这条直线叫做对称轴（axis f symmetry).例如，长方形是有两条对 称轴的轴对称图形，如图1;正方形是有四条对称轴的轴对称图形，如图2; 圆也是轴对称图形，任何过圆心的直线都是它的对称轴，如图3.
〈辽宁阜新〉如图所示的交通标志是轴对称图形的是(　　)
A.是轴对称图形，故本选项正确；B.不是轴对称图形，故本选项错误；C.不是轴对称图形，故本选项错误；D.不是轴对称图形，故本选项错误．
本题运用定义法和排除法解答．根据轴对称图形的定义对各选项分析判断后利用排除法求解．识别轴对称图形的关键是看能否找到一条直线，使图形沿直线折叠后，两侧的部分互相重合．
根据轴对称图形的定义对各选项分析判断后利用排除法求解，识别轴对称图形的关键是看能否找到一条直线，使图形沿直线折叠后，两侧的部分互相重合.
线段、角是轴对称图形吗？如果你认为是轴对称图形，分别说出它 们的对称轴.
(14·天津)下列图形中，为轴对称图形的是(　　)
如图，其中所有轴对称图形的对称轴条数之和为(　　)  A．13 B．11 C．10 D．8
如图 ，AD平分∠BAC,AB=AC.四边形ABDC是轴对称图形吗？如果你认为是，说出它的对称轴.哪一个点与点B对称？
如图 ，AD平分∠BAC , AB=AC.连结BC，交AD于点E.把四边形ABDC沿AD对折，BE与CE重合吗？ ∠ AEB与∠ AEC呢？由此你得到什么结论？
轴对称图形的性质：对称轴________连接两个对称点的线段．
如图，五边形ABCDE是轴对称图形，线段AF所在直线为对称轴，连接BE交AF于点O，找出图中所有相等的线段并判断∠AOB和∠AOE是否相等．
根据轴对称图形的定义和轴对称图形的性质可知，把图形沿AF折叠，重合的线段都相等，重合的角也都相等；AF垂直平分BE和CD.
根据轴对称图形的性质可知，∠AOB＝∠AOE＝90°.
相等的线段：AB＝AE，CB＝DE，CF＝DF，BO＝EO；∠AOB和∠AOE相等．
①对称轴是对应点所连线段的垂直平分线，而不是单单是垂线或平分线；②对应点的连线互相平行（有时在一条直线上）.
如图，以直线l1为对称轴，作点P的对称 点P1;以直线l2为对称轴，作点P的对称 点P2.
P是∠AOB内一点，分别作点P关于直线OA，OB的对称点P1，P2，连结OP1，OP2，则下列结论正确的是(　　)A．OP1⊥OP2 B．OP1＝OP2C．OP1⊥OP2且OP1＝OP2 D．OP1≠OP2
如图，已知直线l是线段AB的对称轴，直线l与AB交于点C，若AB＝10 cm，则AC＝________ cm，BC＝______cm，直线l与AB所成的角的度数是_______．
看下边的照片（图1 ），我们发现照片每两个图形的形状、大小都一样，并且沿着一条直线对折后，这两个图形能够完全重合，我们知道照片是平面图形，我们把这样的两个平面图形叫做成轴对称.那么是不是两个能够重合的图形就成轴对称呢？再把我们的两只手手面朝上向前伸出，一只胳膊伸直，另一只不伸直，然后把两手向内翻，左右手能够重合吗？再看图2中的脚印，你能找到一条直线沿着这条直线折叠后，是脚印重合吗，两个“喜”呢？我们发现两个图形虽然大小相等、形状相同也不一定存在一条直线，沿着这条直线折叠后是这两个图形重合，所以还与位置有关. 如果两个平面图形沿一条直线对折后能够完全重合，那么称这两个图形成轴对称，这条直线叫做这两个图形的对称轴.
一般地，由一个图形变为另一个图形，并使这两个图形沿某一条直线折 叠后能够互相重合，这样的图形改变叫做图形的轴对称(line symmetry)，这条直线叫做对称轴.
〈湖南郴州〉作图题：如图，在方格纸中画出△ABC关于直线MN对称的△A1B1C1.
分别找到A、B、C三点关于直线MN的对称点A1、B1、C1，依次连接A1B1，B1C1，C1A1即可．
给出对称轴，作与已知图形成轴对称的图形的一般方法是：①找出已知图形上的所有关键点的对称点；②按已知图形的形状连接这些对称点，就可得到与已知图形成轴对称的图形．
给出对称轴，作为已知图形成轴对称的图形的一般方法是：①找出已知图形上的所有关键点的对称点；②按已知图形的形状连接这些对称点，就可得到与已知图形成轴对称的图形.
如图，以直线l为对称轴，作与所给图形X成轴对称的图形.
下列选项中的两个图形成轴对称的是(　　)
下列图形中，△A′B′C′与△ABC关于直线MN成轴对称的是(　　)
如图，已知线段AB和直线l.以直线 l为对称轴，作与线段AB成轴对称的图形.
如图，已知直角三角形ABC. (1)以直角边AC所在的直线为对称轴，作出与直角三角形ABC成轴对称的图形.(2)第（1)题作出的图形和原图形组成一个等腰三角形吗？请说明理由.
成轴对称的两个图形是全等图形.
〈湖南怀化〉如图，∠A＝30°，∠C′＝60°，△ABC与△A′B′C′关于直线l对称，则∠B的度数为________．
∵△ABC与△A′B′C′关于直线l对称，∴△ABC≌△A′B′C′，∴∠C＝∠C′＝60°.又∵∠A＝30°，∴∠B＝180°－∠A－∠C＝180°－30°－60°＝90°.
根据图形的轴对称的性质得出△ABC≌△A′B′C′是解答此题的关键．
利用轴对称的性质求线段和角的方法：先根据轴对称的特征确定对应的边，对应的角，然后利用轴对称的性质即对应边相等，对应角相等.把要求的边、角与已知的边、角建立关系式，从而求出待求的边和角.
如图，已知△ABC与△A′B′C′关于直线l成轴对称，且∠A＝45°，∠C′＝35°，则∠B的度数为(　　)A．100° B．90° C．50° D．30°
如图，△ABC和△AB′C′关于直线l对称，下列结论：①△ABC≌△AB′C′；②∠BAC′＝∠B′AC；③直线l垂直平分CC′；④直线BC和B′C′的交点不一定在直线l上．其中正确的有(　　)A．4个 B．3个 C．2个 D．1个
轴对称和轴对称图形的区别与联系联系：(1)都有对称轴，且沿着对称轴对折后能够互相重合；(2)如果把一个轴对称图形沿对称轴分成两个图形，那么这两个图形就关于这条对称轴对称；反过来，如果把成轴对称的两个图形看成一个整体，那么它就是一个轴对称图形．