初中数学人教版九年级上册22.1.1 二次函数图片ppt课件

这是一份初中数学人教版九年级上册22.1.1 二次函数图片ppt课件，共28页。PPT课件主要包含了知识回顾，二次函数，函数知多少，合作交流，a≠0，看谁反应快，知识运用等内容，欢迎下载使用。

１、什么叫函数?
在某变化过程中的两个变量x、y，当变量x在某个范围内取一个确定的值，另一个变量y总有唯一的值与它对应。 这样的两个变量之间的关系我们把它叫做函数关系。 对于上述变量x 、y，x叫自变量，我们把y叫x的函数。
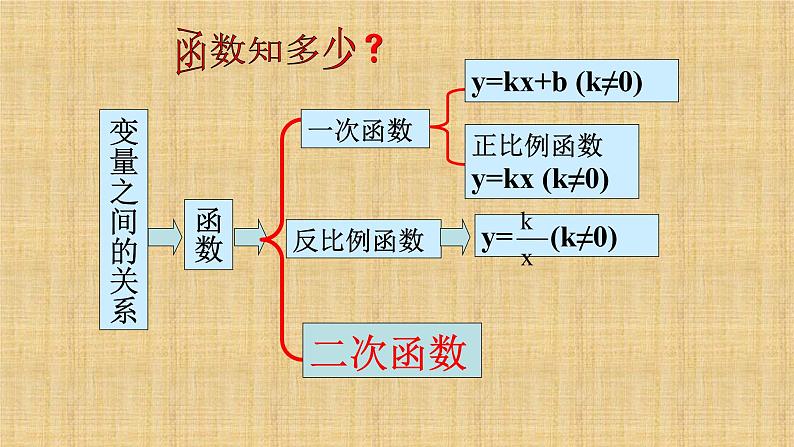
目前，我们已经学习了那几种类型的函数？
正方体的六个面是全等的正方形,设正方形的棱长为x,表面积为y,显然对于x的每一个值,y都有一个对应值,即y是x的函数,它们的具体关系可以表示为
多边形的对角线数d与边数n有什么关系？
由图可以想出,如果多边形有n条边,那么它有 个顶点,从一个顶点出发,连接与这点不相邻的各顶点,可以作 条对角线.
因为像线段MN与NM那样,连接相同两顶点的对角线是同一条对角线,所以多边形的对角线总数
函数①②③有什么共同点?
在上面的问题中,函数都是用自变量的二次式表示的。
定义：一般地，形如y=ax²+bx+c(a,b,c是常数,a≠ 0)的函数叫做二次函数。其中x是自变量，a为二次项系数，ax2叫做二次项，b为一次项系数，bx叫做一次项，c为常数项。
（1）等号左边是变量y，右边是关于自变量 x的
（3）等式的右边最高次数为 ，可以没有一次项和常数项，但不能没有二次项。
（2）a,b,c为常数，且
（4）x的取值范围是任意实数。
（5）函数的右边是一个 整 式
y＝ax2＋bx＋c (其中a、b、c是常数,a≠0)二次函数的特殊形式：1.当b＝0时， y＝ax2＋c2.当c＝0时， y＝ax2＋bx3.当b＝0，c＝0时， y＝ax2
1、 说出下列二次函数的二次项系数、一次项系数、常数项.
（1） y=-x2+58x-112
2、指出下列函数y=ax²+bx+c中的a、b、c.
（1） y=-3x2-x-1
（3） y=x(1+x)
（2） y=5x2-6
例1、下列函数中，哪些是二次函数？若是,分别指出二次项系数,一次项系数,常数项。 (1) y=3(x－1)²+1 (2) y=x+ (3) s=3－2t² (4) y=(x+3)²－x² (5)y= －x (6) v=8π r²
y=3(x-1)²+1 =3(x2-2x+1)+1 =3x2-6x+3+1即
(3) s=3-2t²是二次函数.
(4) y=(x+3)²-x²=x2+6x+9-x2即
(6) v=8π r²
解：（１）当m2－7=1且m+3≠0即m=± 　时是正比例函数。
（２）当m2－7=-1且m+3≠0即m=± 时是反比例函数。
（３）当m2－7=2且m+3≠0即m=3 时是二次函数。
例３、某宾馆有50个房间供游客住宿，当每个房间的房价为每天180元时，房间会全部住满．当每个房间每天的房价每增加10元时，就会有一个房间空闲．宾馆需对游客居住的每个房间每天支出20元的各种费用．根据规定，每个房间每天的房价不得高于340元．设每个房间的房价每天增加x元（x为10的整数倍）． （1）设一天订住的房间数为y，直接写出y与x的函数关系式及自变量x的取值范围； （2）设宾馆一天的利润为W元，求W与x的函数关系式；
解：（1）由题意得： y=50-    ，且0≤x≤160，且x为10的正整数倍． （2）w=（180-20+x）（50-    ），即w=-    x2+34x+8000；
思考：2. 二次函数的一般式y＝ax2＋bx＋c（a≠0）与一元二次方程ax２＋bx＋c＝0（a≠0）有什么联系和区别？
联系(1)等式一边都是ax2＋bx＋c且 a ≠0(2)方程ax2＋bx＋c=0可以看成是函数y= ax2＋bx＋c中y=0时得到的.
区别:前者是函数.后者是方程.等式另一边前者是y,后者是0
1:下列函数中，哪些是二次函数？ (1)y=3x-1 ( ) (2)y=3x2 （ ) (3)y=3x3+2x2 ( ) (4)y=2x2-2x+1( ) (5)y=x-2+x ( ) (6)y=x2-x(1+x) ( )
m2—2m-1=2 m+1 ≠0 ∴m=3
一次函数y=kx+b (k ≠0),其中包括正比例函数 y=kx(k≠0), 反比例函数y= (k≠0) ， 二次函数y=ax2+bx+c(a≠0)。
现在我们学习过的函数有:
可以发现,这些函数的名称都形象地反映了函数表达式与自变量的关系。
２.函数 y=(m-n)x2+ mx+n 是二次函数的条件是( )A m,n是常数,且m≠0 B m,n是常数,且n≠0C m,n是常数,且m≠n D m,n为任何实数
３.一个圆柱的高等于底面半径,写出它的表面积 s 与半径 r 之间的关系式.４. n支球队参加比赛,每两队之间进行一场比赛,写出比赛的场次数 m与球队数 n 之间的关系式.
S=2πr2 +2πr2 即S=4πr2
５、 一农民用40m长的篱笆围成一个一边靠墙的长方形菜园，和墙垂直的一边长为Xm，菜园的面积为Ym2，求y与x之间的函数关系式，并说出自变量的取值范围。当x=12m时，计算菜园的面积。
（40-2x ）m
Y=x(40-2x)
即：Y=-2x2+40x
当x＝12m时，菜园的面积为：
Y=-2x2+40x＝-2×122+40×12 ＝192（m2）