初中数学鲁教版 (五四制)八年级上册第五章 平行四边形2 平行四边形的判定习题ppt课件

这是一份初中数学鲁教版 (五四制)八年级上册第五章 平行四边形2 平行四边形的判定习题ppt课件，共28页。PPT课件主要包含了答案呈现，习题链接等内容，欢迎下载使用。

【中考·牡丹江】如图，四边形ABCD的对角线AC，BD相交于点O，AO＝CO，请添加一个条件：_____________________(只添一个即可)，使四边形ABCD是平行四边形．
BO＝DO(答案不唯一)
【点拨】因为对角线互相平分的四边形是平行四边形，所以添加条件BO＝DO，可判定四边形ABCD是平行四边形．
【中考·泸州】四边形ABCD的对角线AC与BD相交于点O，下列四组条件中，一定能判定四边形ABCD为平行四边形的是(　　)A．AD∥BC B．OA＝OC，OB＝ODC．AD∥BC，AB＝DC D．AC⊥BD
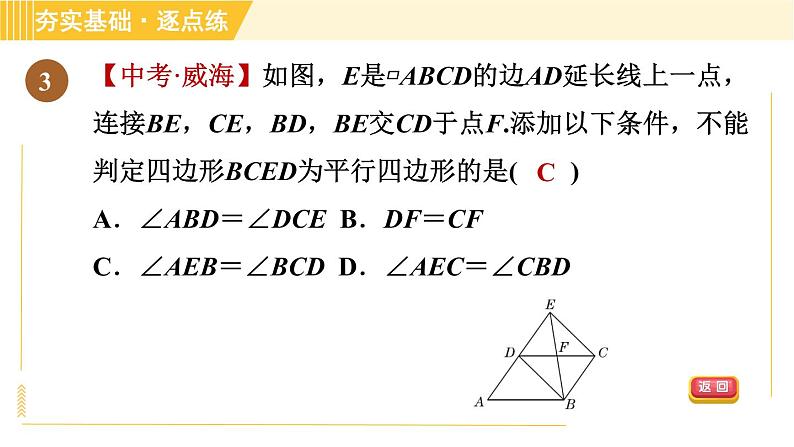
【中考·威海】如图，E是▱ABCD的边AD延长线上一点，连接BE，CE，BD，BE交CD于点F.添加以下条件，不能判定四边形BCED为平行四边形的是(　　)A．∠ABD＝∠DCE B．DF＝CFC．∠AEB＝∠BCD D．∠AEC＝∠CBD
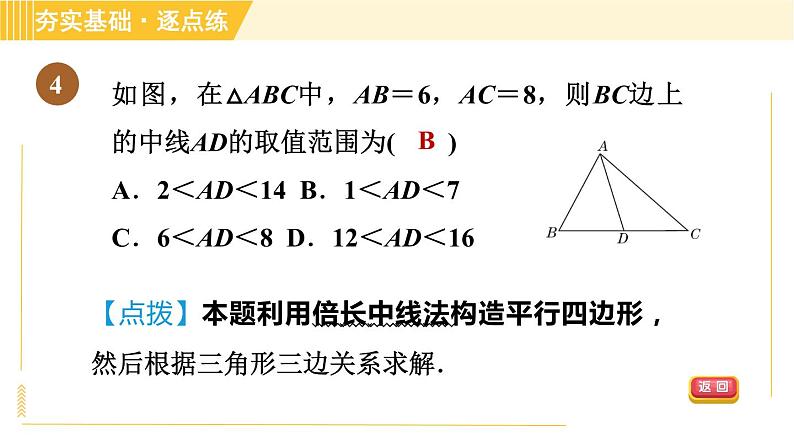
如图，在△ABC中，AB＝6，AC＝8，则BC边上的中线AD的取值范围为(　　)A．2＜AD＜14 B．1＜AD＜7C．6＜AD＜8 D．12＜AD＜16
【点拨】本题利用倍长中线法构造平行四边形，然后根据三角形三边关系求解．
【中考·湘西州】下列说法错误的是(　　)A．对角线互相平分的四边形是平行四边形B．两组对边分别相等的四边形是平行四边形C．一组对边平行且相等的四边形是平行四边形D．一组对边相等，另一组对边平行的四边形是平行四边形
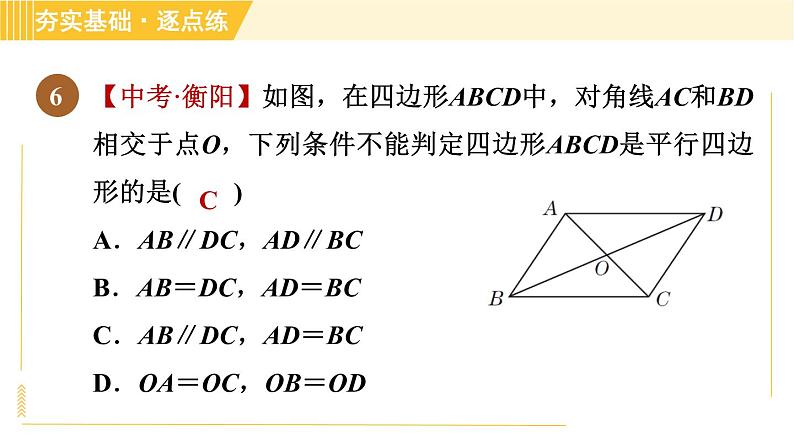
【中考·衡阳】如图，在四边形ABCD中，对角线AC和BD相交于点O，下列条件不能判定四边形ABCD是平行四边形的是(　　)A．AB∥DC，AD∥BC B．AB＝DC，AD＝BCC．AB∥DC，AD＝BCD．OA＝OC，OB＝OD
【点拨】∵AB∥DC，AD∥BC，∴四边形ABCD是平行四边形，故选项A中的条件可以判定四边形ABCD是平行四边形；∵AB＝DC，AD＝BC，∴四边形ABCD是平行四边形，故选项B中的条件可以判定四边形ABCD是平行四边形；由AB∥DC，AD＝BC无法判定四边形ABCD是平行四边形，故选项C中的条件不能判定四边形ABCD是平行四边形；∵OA＝OC，OB＝OD，∴四边形ABCD是平行四边形，故选项D中的条件可以判定四边形ABCD是平行四边形．故选C.
如图，在▱ABCD中，E，F分别是AD，BC边的中点，G，H是对角线BD上的两点，且BG＝DH，则下列结论中不一定成立的是(　　)A．GF⊥FH B．GF＝EHC．EF与AC互相平分 D．EG＝FH
【点拨】设AC，BD的交点为O，则OA＝OC，OB＝OD，EF过点O.∵BG＝DH，∴HO＝OG.易证△AOE≌△COF，∴OE＝OF.∴四边形EHFG是平行四边形，∴GF＝EH，EG＝FH.故选A.
如图，在▱ABCD中，对角线AC，BD相交于O，E，F是对角线AC上的两点，给出下列4个条件：①OE＝OF；②DE＝BF；③∠ADE＝∠CBF；④∠ABE＝∠CDF.其中不能判定四边形DEBF是平行四边形的有(　　)A．0个 B．1个C．2个 D．3个
【点拨】给出条件①OE＝OF，由四边形ABCD是平行四边形，可得OD＝OB.又∵OE＝OF，∴四边形DEBF为平行四边形．故①正确．给出条件③∠ADE＝∠CBF，∵四边形ABCD是平行四边形，∴AD＝CB，AD∥CB.∴∠DAE＝∠BCF.
又∵∠ADE＝∠CBF，∴△ADE≌△CBF.∴DE＝BF，∠AED＝∠CFB.∴∠DEO＝∠BFO.∴DE∥BF.∴四边形DEBF为平行四边形．故③正确．给出条件④∠ABE＝∠CDF，理由同③，亦可判定四边形DEBF为平行四边形．故④正确．只有给出条件②无法判定四边形DEBF为平行四边形．故选B.
如图，在▱ABCD中，分别过A，C两点作对角线BD的垂线，垂足分别为M，N.连接AN，CM.求证：(1)BM＝DN；
(2)四边形AMCN为平行四边形．
解:连接AC交BD于点O.在▱ABCD中，OA＝OC，OB＝OD.∵BM＝DN，∴BM－OB＝DN－OD，∴OM＝ON，∴四边形AMCN为平行四边形．
如图，四边形ABCD中，对角线AC，BD相交于点O，点E，F分别在OA，OC上．(1)给出以下条件：①OB＝OD；②∠1＝∠2；③OE＝OF.请你从中选取两个条件证明△BEO≌△DFO.
(2)在(1)中你所选条件的前提下，添加AE＝CF，求证：四边形ABCD是平行四边形．
解：由(1)得△BEO≌△DFO，∴EO＝FO.∵AE＝CF，∴AO＝CO.又∵BO＝DO，∴四边形ABCD是平行四边形．
【中考·大庆】如图，在以BC为底边的等腰三角形ABC中，点D，E，G分别在BC，AB，AC上，且EG∥BC，DE∥AC，延长GE至点F，使得BF＝BE.(1)求证：四边形BDEF为平行四边形；
证明：∵三角形ABC是以BC为底边的等腰三角形，∴∠ABC＝∠C.∵EG∥BC，DE∥AC，∴四边形CDEG是平行四边形．∴∠DEG＝∠C.∵EG∥BC，∴∠AEG＝∠ABC.∴∠DEG＝∠AEG.∵BE＝BF，∴∠BFE＝∠BEF＝∠AEG.∴∠BFE＝∠DEG.∴BF∥DE.∴四边形BDEF为平行四边形．
(2)当∠C＝45°，BD＝2时，求D，F两点间的距离．
解：∵DE∥AC，∴∠BDE＝∠C.∵∠C＝45°，∴∠BDE＝∠ABC＝∠BEF＝∠BFE＝45°.∴△BDE，△BEF都是等腰直角三角形．
如图，在▱ABCD中，∠DAB＝60°，点E，F分别在CD，AB的延长线上，且AE＝AD，CF＝CB.(1)求证：四边形AFCE是平行四边形．
证明：∵四边形ABCD是平行四边形，∴DC∥AB，∠DCB＝∠DAB＝60°.∴∠ADE＝∠CBF＝60°.∵AE＝AD，CF＝CB，∴△AED，△CFB是等边三角形．∴∠AEC＝∠DAE＝∠BCF＝∠BFC＝60°，∴∠EAF＝∠FCE＝120°.易得AE∥FC，AF∥EC，∴四边形AFCE是平行四边形．
(2)若去掉已知条件“∠DAB＝60°”，上述结论还成立吗？若成立，请写出证明过程；若不成立，请说明理由．
解：上述结论还成立．证明：∵四边形ABCD是平行四边形，∴DC＝AB，AD＝BC，∠ADC＝∠ABC.∴∠ADE＝∠CBF.