重庆市铜梁区2020-2021学年七年级下学期期末数学试题（word版含答案）

展开

这是一份重庆市铜梁区2020-2021学年七年级下学期期末数学试题（word版含答案），共21页。试卷主要包含了单选题，填空题，解答题等内容，欢迎下载使用。

重庆市铜梁区2020-2021学年七年级下学期期末数学试题
学校:___________姓名：___________班级：___________考号：___________

一、单选题
1．给出四个实数，，，，其中为无理数的是( )
A．2 B．-1 C． D．
2．点M(-2，4)到x轴的距离是( )
A．4 B．-4 C．2 D．-2
3．若a A．ab<0 B．ab>0 C．a－b>0 D．－a>－b
4．下列调查中，适宜采用全面调查（普查）方式的是（）
A．了解我国民众对“乐天萨德事件”的看法
B．了解浙江卫视“奔跑吧兄弟”节目的收视率
C．调查我校某班学生喜欢上数学课的情况
D．调查某类烟花爆竹燃放的安全情况
5．在数轴上表示不等式的解集，正确的是( )
A． B． C． D．
6．方程组，由②-①，得到的方程是( )
A． B． C． D．
7．如图，已知，，则( )

A． B． C． D．
8．若，则估计m的值所在的范围是（）
A． B． C． D．
9．已知是二元一次方程组的解，则的值为
A．－1 B．1 C．2 D．3
10．下列四个命题中，假命题的是（）
A．在同一平面内，如果两条直线都垂直于同一条直线，那么这两条直线平行
B．在数轴上，一个实数的绝对值越大，则表示这个数的点在数轴上离原点越远，越靠右
C．坐标平面内的点，与有序实数对是一一对应的
D．经过两点有一条直线，并且只有一条直线
11．扬州某中学七年级一班 40 名同学第二次为四川灾区捐款，共捐款 2000 元，捐款情况如下表：
捐款（元）
20
40
50
100
人数
10

8
表格中捐款 40 元和 50 元的人数不小心被墨水污染已看不清楚、若设捐款 40 元的有 x 名同学，捐款 50 元的有y 名同学，根据题意，可得方程组（）
A． B．
C． D．
12．若关于的不等式组有解，且关于的方程有非负整数解，则符合条件的所有整数的和为( )
A．-5 B．-9 C．-12 D．-16

二、填空题
13．点P(-3，-2)在第_____象限.
14．方程组的解是_______________.
15．某校在开展创办“特色学校”前夕，从该校七年级共400名学生中，随机抽取40名学生进行“你最喜欢的活动”问卷调查，在这个问题中，样本容量是________.
16．计算： ________________________．
17．关于、的二元一次方程组的解满足不等式，则的取值范围是__.
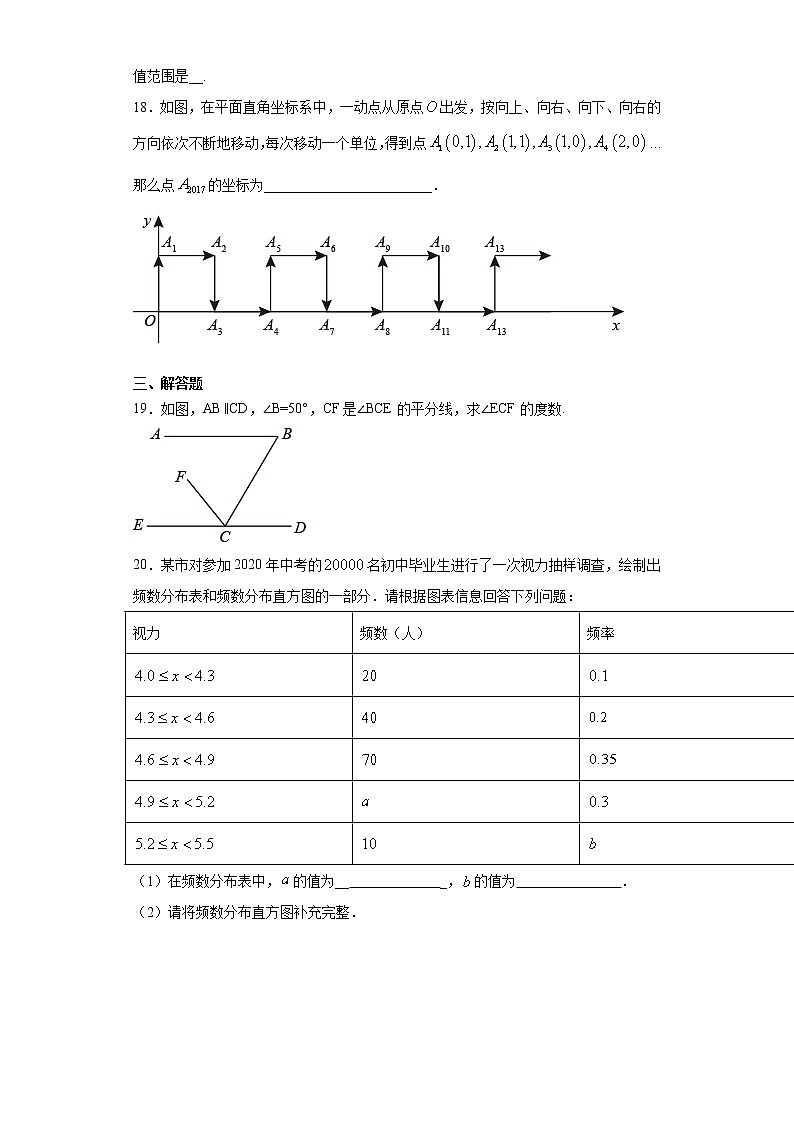
18．如图，在平面直角坐标系中，一动点从原点出发，按向上、向右、向下、向右的方向依次不断地移动，每次移动一个单位，得到点…那么点的坐标为________________________．

三、解答题
19．如图，AB∥CD，∠B=50°，CF是∠BCE的平分线，求∠ECF的度数.

20．某市对参加2020年中考的名初中毕业生进行了一次视力抽样调查，绘制出频数分布表和频数分布直方图的一部分．请根据图表信息回答下列问题：
视力
频数（人）
频率

（1）在频数分布表中，的值为__ _，的值为．
（2）请将频数分布直方图补充完整．

（3）若视力在以上（含）均属正常，根据上述信息估计全市初中毕业生中视力正常的学生有多少人？
21．(1)解方程组
(2)解不等式组
22．如图所示在平面直角坐标系中，方格纸中每个小方格都是边长为1个单位长度的正方形，已知点，，.

（1）在所给的直角坐标系中画出三角形；
（2）把三角形向左平移3个单位，再向上平移2个单位得到三角形，画出三角形并写出点的坐标；
（3）求三角形的面积.
23．请把下列证明过程补充完整.已知:如图，B、C、E三点在同一直线上，A、F、E三点在同一直线上，∠1=∠2=∠E，∠3=∠4.求证:AB∥CD．

证明:∵∠2=∠E(已知)
∴ ∥BC( )
∴∠3=∠ ( )
∵∠3=∠4(已知)
∴∠4=∠ ( )
∵∠1=∠2(已知)
∴∠1+∠CAF=∠2+∠CAF ，即∠BAF=∠
∴∠4=∠ (等量代换)
∴ ( )
24．一个四位数，记千位上和百位上的数字之和为x，十位上和个位上的数字之和为y，如果x=y，那么称这个四位数为“和平数”.例如:1423，x=1+4，y=2+3，因为x=y，所以1423是“和平数”.
(1)请判断:2561 (填“是”或“不是”)“和平数”
(2)直接写出:最小的“和平数”是，最大的“和平数”是
(3)如果一个“和平数”的个位上的数字是千位上的数字的两倍，且百位上的数字与十位上的数字之和是14的倍数，求满足条件的所有“和平数”.
25．今年6月初，由于持续暴雨，某市遭受严重水涝灾害，群众失去家园，市民政局为解决灾民困难，紧急组织了一批救灾帐篷和食品准备送往灾区．已知这批物质中，帐篷和食品共件，且帐篷比食品多件．
（1）求帐篷和食品各有多少件？
（2）现计划租用两种货车共辆，一次性将这批物质全部送到灾民手中，已知两种货车可装帐篷和食品的件数以及每辆货车所需付运费情况如下表，求出运费最少的方案？最少运费是多少？

帐篷（件）
食品（件）
每辆需付运费（元）
种货车

种货车

26．如图，在平面直角坐标系中，点A，B的坐标分别为A(a，0)，B(b，0).且a，b满足+(a-2b+7)2=0.现同时将点A，B分别向左平移2个单位，再向上平移2个单位，分别得到点A，B的对应点C，D，连接AC，BD．
(1)请直接写出A，B两点的坐标.
(2)如图，点P是线段AC上的一个动点，点Q是线段CD的中点，连接PQ，PO，当点P在线段AC上移动时(不与A，C重合)，请找出∠PQD，∠OPQ，∠POB的数量关系，并证明你的结论.
(3)在坐标轴上是否存在点M，使三角形MAD的面积与三角形ACD的面积相等？若存在，直接写出点M的坐标；若不存在，试说明理由.

参考答案
1．C
【分析】
分别根据无理数、有理数的定义即可判定选择项．
【详解】
解：2，-1，是有理数，
-是无理数，
故选C．
【点睛】
此题主要考查了无理数的定义，注意带根号的要开不尽方才是无理数，无限不循环小数为无理数．如π，，0.8080080008…（每两个8之间依次多1个0）等形式．
2．A
【详解】
解：点M（-2，4）到x轴的距离是4．
故选A．
【点睛】
本题考查了点的坐标，熟记点到x轴的距离等于点的纵坐标的绝对值是解题的关键．
3．D
【分析】
A、B利用举反例的方法，C、D利用不等式的基本性质判定．
【详解】
解：A、若，则，
B、若，则，
C、，故A、B、C选项错误；
D、由得，本选项正确.
【点睛】
本题考查不等式的基本性质．本题属于基础应用题，只需学生熟练掌握不等式的基本性质，即可完成.
4．C
【分析】
由题意根据普查得到的调查结果比较准确，但所费人力、物力和时间较多，而抽样调查得到的调查结果比较近似判断即可．
【详解】
解：A、了解我国民众对“乐天萨德事件”的看法调查范围广适合抽样调查，故A不符合题意；
B、了解浙江卫视“奔跑吧兄弟”节目的收视率调查范围广适合抽样调查，故B不符合题意；
C、调查我校某班学生喜欢上数学课的情况适合普查，故C符合题意；
D、调查某类烟花爆竹燃放的安全情况调查具有破坏性适合抽样调查，故D不符合题意；
故选：C．
【点睛】
本题考查的是抽样调查和全面调查的区别，选择普查还是抽样调查要根据所要考查的对象的特征灵活选用，一般来说，对于具有破坏性的调查、无法进行普查、普查的意义或价值不大，应选择抽样调查，对于精确度要求高的调查，事关重大的调查往往选用普查．
5．B
【分析】
求出不等式的解集，表示在数轴上即可．
【详解】
解：不等式x+5≥1，
解得：x≥-4，
表示在数轴上，如图所示：

故选B．
【点睛】
此题考查了在数轴上表示不等式的解集，把每个不等式的解集在数轴上表示出来（＞，≥向右画；＜，≤向左画），数轴上的点把数轴分成若干段，如果数轴的某一段上面表示解集的线的条数与不等式的个数一样，那么这段就是不等式组的解集．有几个就要几个．在表示解集时“≥”，“≤”要用实心圆点表示；“＜”，“＞”要用空心圆点表示．
6．C
【分析】
②-①的过程其实是合并同类项得过程，依据合并同类项法则解答即可．
【详解】
解：
由②-①，得
x=5．
故选C．
【点睛】
这类题目的解题关键是掌握方程组解法中的加减消元法．
7．D
【分析】
根据平行线的判定推出a∥b，根据平行线的性质得出∠1+∠4=180°即可．
【详解】
解：如图，

∵∠2+∠3=180°，
∴a∥b，
∴∠1=∠5，
∵∠1=120°，
∴∠5=120°，
∴∠4=180°-120°=60°，
故选D．
【点睛】
本题考查了平行线的性质和判定，注意：①同旁内角互补，两直线平行，②两直线平行，同位角相等．
8．C
【分析】
根据的取值范围得出m的取值范围．
【详解】
解：∵，
∴．
故选：C．
【点睛】
本题考查无理数的估算，解题的关键是掌握估算无理数的求法．
9．A
【详解】
试题分析：∵已知是二元一次方程组的解，
∴
由①+②，得a=2，
由①-②，得b=3，
∴a-b=-1；
故选A．
考点：二元一次方程的解．
10．B
【分析】
由题意根据平行线的判定定理、数轴的概念、直线的性质、平面直角坐标系进行分析判断即可．
【详解】
解：A、在同一平面内，如果两条直线都垂直于同一条直线，那么这两条直线平行是真命题；
B、在数轴上，一个实数的绝对值越大，则表示这个数的点在数轴上离原点越远，这个数如果是负数，则越靠左，如果是正数，则越靠右，故B是假命题；
C、坐标平面内的点，与有序实数对是一一对应的是真命题；
D、经过两点有一条直线，并且只有一条直线是真命题；
故选：B．
【点睛】
本题考查的是命题的真假判断，正确的命题叫真命题，错误的命题叫做假命题．判断命题的真假关键是要熟悉课本中的性质定理．
11．C
【分析】
两个定量：捐40元和50元的总人数，捐40元和50元的总钱数．
等量关系为：①捐40元和50元的总人数=40-10-8名同学；
②捐40元和50元的总钱数=2000-20×10-100×8．
【详解】
解：根据七年级一班有40名同学，得方程x+y=40-10-8，即x+y=22；
根据题意，得方程40x+50y=2000-20×10-100×8，40x+50y=1000．
列方程组为．
故选C．
【点睛】
读懂题意，找到捐40元和50元的总人数和捐40元和50元的总钱数列出方式是解答本题的关键．
12．B
【分析】
先根据不等式组有解得k的取值，利用方程有非负整数解，将k的取值代入，找出符合条件的k值，并相加．
【详解】
，
解①得：x≥1+4k，
解②得：x≤6+5k，
∴不等式组的解集为：1+4k≤x≤6+5k，
1+4k≤6+5k，
k≥-5，
解关于x的方程kx=2（x-2）-（3x+2）得，x=-，
因为关于x的方程kx=2（x-2）-（3x+2）有非负整数解，
当k=-4时，x=2，
当k=-3时，x=3，
当k=-2时，x=6，
∴-4-3-2=-9；
故选B．
【点睛】
本题考查了解一元一次不等式组、方程的解，有难度，熟练掌握不等式组的解法是解题的关键．
13．三
【分析】
应先判断出点的横纵坐标的符号，进而判断其所在的象限．
【详解】
点P的横坐标-3＜0，纵坐标-2＜0，则点在第三象限．故答案为三．
【点睛】
本题主要考查第三象限内点的坐标的符号．解决本题的关键是记住平面直角坐标系中各个象限内点的符号．
14．
【分析】
根据解二元一次方程组的方法可以解答此方程组．
【详解】
解：，
由①，得
x=3，
将x=3代入②，得
y=-1，
故原方程组的解是，
故答案为．
【点睛】
本题考查解二元一次方程组，解答本题的关键是明确解二元一次方程组的方法．
15．40
【分析】
根据样本容量：一个样本包括的个体数量叫做样本容量可得答案．
【详解】
解：某校在开展创办“特色学校”前夕，从该校七年级共400名学生中，随机抽取40名学生进行“你最喜欢的活动”问卷调查，在这个问题中，样本容量是40，
故答案为40．
【点睛】
此题主要考查了样本容量，关键是注意样本容量只是个数字，没有单位．
16．
【分析】
由题意根据乘方的运算和算术平方根和立方根性质进行运算即可得出答案.
【详解】
解：

故答案为：.
【点睛】
本题考查实数的运算，熟练掌握乘方的运算法则和算术平方根和立方根性质是解题的关键.
17．
【分析】
将两方程相加可得4x+4y=2+2a，即x+y=＞0，解之可得答案．
【详解】
解：将两方程相加可得4x+4y=2+2a，
则x+y=，
由x+y＞0可得＞0，
解得a＞-1，
故答案为a＞-1．
【点睛】
本题主要考查解一元一次不等式的能力，解题的关键是根据题意列出关于a的不等式．
18．
【分析】
先求出前几个点的坐标，然后根据点的坐标找到规律，由此即可求得点的坐标．
【详解】
根据题意和图的坐标可知：每次都移动一个单位长度，图中按向上、向右、向下、向右的方向依次不断地移动、、、、、、…
∴坐标变化的规律：每移动4次，它的纵坐标都为1，而横坐标向右移动了2个单位长度，也就是移动次数的一半；
∴2017÷4=504…1
∴纵坐标是的纵坐标1；
∴横坐标是0+2×504=1008，
∴点的坐标为(1008，1) ．
故答案为：．
【点睛】
本题考查点坐标规律探索、学生的数形结合和归纳能力，仔细观察图象，找到点的坐标的变化规律是解答的关键．
19．
【分析】
根据平行线的性质，可得∠BCE=180°-∠B=130°，再根据CF是∠BCE的平分线，即可得出∠ECF=∠BCE=65°．
【详解】
解：∵AB∥CD，∠B=50°，
∴∠BCE=180°-∠B=130°，
∵CF是∠BCE的平分线，
∴∠ECF=∠BCE=65°．
【点睛】
本题考查了对平行线性质和角平分线定义的应用，注意：两直线平行，同旁内角互补．
20．（1）60，0.05；（2）见解析；（3）7000人
【分析】
（1）根据第一组的频数是20，对应的频率是0.1即可求得总人数，然后利用频率的概念求得a、b的值；
（2）根据中位数的定义即可作出判断；
（3）用样本值后面三组的频率和乘以20000可估计全区初中毕业生中视力正常的学生数．
【详解】
解：（1）抽查的总人数是：20÷0.1=200（人），
则a=200×0.3=60，b==0.05．
故答案是：60，0.05；
（2）如图，
；
（3）20000×（0.3+0.05）=7000（人），
估计全区初中毕业生中视力正常的学生有7000人．
【点睛】
本题考查读频数分布直方图的能力和利用统计图获取信息的能力；利用统计图获取信息时，必须认真观察、分析、研究统计图，才能作出正确的判断和解决问题
21．（1）；（2）
【分析】
（1）①-②×5得出-27y=-27，求出y，把y=1代入②求出x即可；
（2）先求出不等式的解集，再求出不等式组的解集即可．
【详解】
解：（1）
①-②×5得：-27y=-27，
解得：y=1，
把y=1代入②得：x+5=6，
解得：x=1，
所以原方程组的解为；
（2）
∵解不等式①得：x＜3，
解不等式②得：x≥，
∴不等式组的解集为：≤x＜3．
【点睛】
本题考查了解二元一次方程组和解一元一次不等式组，能把二元一次方程组转化成一元一次方程是解（1）的关键，能根据不等式的解集求出不等式组的解集是解（2）的关键．
22．（1）见解析；（2）见解析，C′（0，4）；（3）5.
【分析】
（1）根据网格结构找出点A、B、C的位置，然后顺次连接即可；
（2）根据网格结构找出点A、B、C向左平移3个单位，再向上平移2个单位后对应点A′、B′、C′的位置，然后顺次连接即可，再根据平面直角坐标系写出点C′的坐标；
（3）根据三角形的面积公式列式计算即可得解．
【详解】
解：（1）△ABC如图所示；
（2）△A′B′C′如图所示，C′（0，4）；

（3）△A′B′C′的面积＝×5×2＝5．
【点睛】
本题考查了利用平移变换作图，三角形的面积，熟练掌握网格结构准确找出对应点的位置是解题的关键．
23．见解析
【分析】
根据平行线的判定可得AD∥BC，根据平行线的性质和等量关系可得∠4=∠BAC，再根据平行线的判定可得AB∥CD．
【详解】
∵∠2=∠E（已知）
∴AD∥BC（内错角相等，两直线平行）
∴∠3=∠DAC（两直线平行，内错角相等）
∵∠3=∠4（已知）
∴∠4=∠DAC（等量关系）
∵∠1=∠2（已知）
∴∠1+∠CAF=∠2+∠CAF
即∠BAF=∠DAC
∴∠4=∠BAC（等量代换）
∴AB∥CD（同位角相等，两直线平行）
故答案为AD，内错角相等，两直线平行；DAC，两直线平行，内错角相等；DAC，等量关系；DAC，BAF；AB∥CD，同位角相等，两直线平行．
【点睛】
本题考查了平行线的判定：同位角相等，两直线平行；内错角相等，两直线平行；同旁内角互补，两直线平行．
24．（1）是；（2）1001，9999；（3）满足条件的“和平数”为2864或4958
【详解】
分析：（1）根据“和平数”的定义计算x和y的值，即可得到结论；
（2）根据题意可得结论；
（3）设这个“和平数”为，于是得到d=2a，a+b=c+d，b+c=14k，求得2c+a=14k，即得a和d的可能的值，分情况讨论：得到结论，注意每个数位上的数都是一位整数．
详解：（1）∵x=2+5=7，y=6+1=7
∴x=y
∴2561是“和平数”
故答案为是；
（2）由题意得，最小的“和平数”是1001，最大的“和平数”是9999，
故答案为1001，9999；
（3）设这个“和平数”为，
则d=2a，a+b=c+d，b+c=14k，
∴2c+a=14k，
即a=2、4，6，8，d=4、8、12（舍去）、16（舍去），
①当a=2，d=4时，2（c+1）=14k，
可知c+1=7k且a+b=c+d，
∴c=6，b=8，
②当a=4，d=8时，
2（c+2）=14k，
可知c+2=7k且a+b=c+d，
∴c=5，b=9，
综上所述，这个数为2864和4958．
点睛：本题考查了因式分解的应用，正确的理解新概念“和平数”是解题的关键，并注意数位上数字的特点．
25．（1）这批物质中帐篷有件，食品有件；（2）租用种货车共辆，租用种货车辆，所需付运费最少，最少运费为元
【分析】
（1）设食品x件，则帐篷（x+80）件，根据帐篷和食品共320件建立方程求出其解即可；
（2）设租用A种货车a辆，则B种货车（8-a）辆，根据帐篷和食品的数量建立不等式组求出运输方案，再分别计算出每种方案的运费，然后比较得出结果．
【详解】
解：解：（1）设食品x件，则帐篷（x+80）件，由题意，得
x+（x+80）=320，
解得：x=120．
则帐篷有120+80=200件．
答：食品120件，则帐篷200件；
（2）设租用A种货车a辆，则B种货车（8-a）辆，由题意，得
，
解得：2≤a≤4．
∵a为整数，
∴a=2，3，4．
∴B种货车为：6，5，4．
∴方案有3种：
方案一：A车2辆，B车6辆；
方案二：A车3辆，B车5辆；
方案三：A车4辆，B车4辆；
3种方案的运费分别为：
①2×780+6×700=5760（元）；
②3×780+5×700=5840（元）；
③4×780+4×700=5920（元）．
则方案①运费最少，最少运费是5760元．
【点睛】
本题考查了列一元一次方程解实际问题的运用和一元一次不等式组的运用，解答时根据条件提供的数量关系建立方程和不等式组是解答本题的关键．
26．(1) A(-3，0) B(2，0);
【分析】
（1）根据平方与绝对值的非负性即可求解；（2）过点P作PE∥AB，由平移的性质可得AB∥CD，利用平行线的性质即可求解；（3）先求出△ACD的面积，再根据M在x轴上与y轴上分别求解.
【详解】
解:(1)依题意得=0，a-2b+7=0，解得a=-3，b=2，
∴A(-3，0) B(2，0)
∵将点A，B分别向左平移2个单位，再向上平移2个单位，分别得到点A，B的对应点C，D，
∴C（-5,2），D（0,2）
(2)∠PQD+∠OPQ+∠POB=360°
证明:过点P作PE∥AB，由平移的性质可得AB∥CD，
∴AB∥PE∥CD，
∴∠PQD+∠EPQ =180°，∠OPE +∠POB=180°，
∴∠PQD+∠EPQ+∠OPE +∠POB=360°，
即∠PQD+∠OPQ+∠POB=360°
(3) 先求出△ACD的面积为=5
①M在x轴上
再根据△MAD的高与△ACD相等即AM=CD=5，故坐标为(-8，0)，(2，0)，
②M在y轴上，根据△MAD的高为AO=3，得出MD=
由D（0,2）
得出M(0，)，(0，).
故存在符合条件的M点坐标为(-8，0)，(2，0)，(0，)，(0，).

【点睛】
此题主要考查直角坐标系的坐标特点，解题的关键是熟知坐标的平移与面积的计算.