初中北京课改版21.4 圆周角图文ppt课件

这是一份初中北京课改版21.4 圆周角图文ppt课件，共21页。PPT课件主要包含了在圆上，圆周角定理，推论1，定理应用，巩固练习，课堂小结与反思，课堂达标检测等内容，欢迎下载使用。

学习目标:1.理解圆周角的概念。2.探索圆周角与圆心角及其所对弧的关系，了解并证明圆周角定理及其推论。
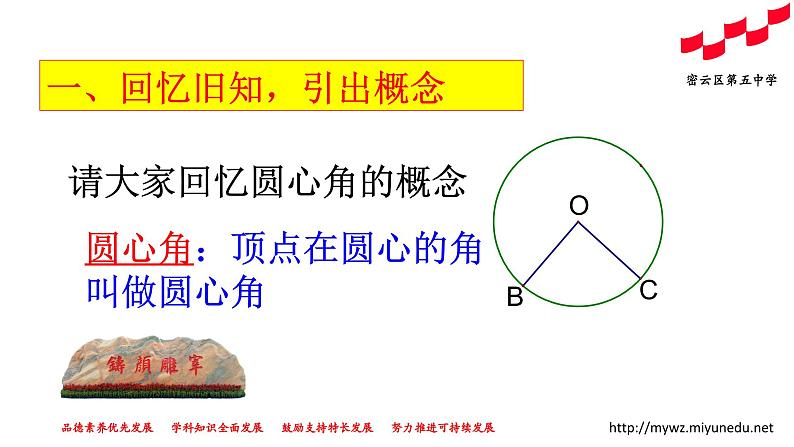
一、回忆旧知，引出概念
请大家回忆圆心角的概念
圆心角：顶点在圆心的角叫做圆心角
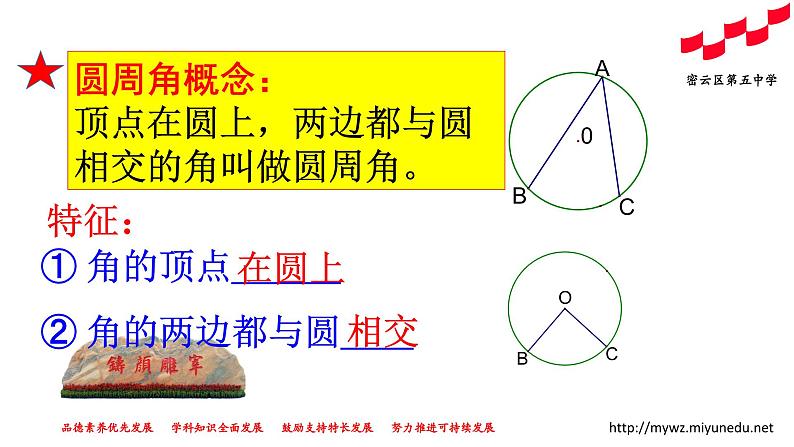
① 角的顶点＿＿＿ ② 角的两边都与圆＿＿
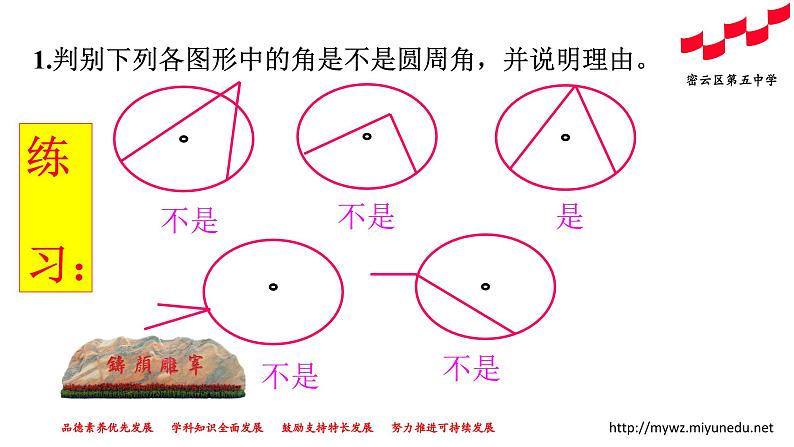
1.判别下列各图形中的角是不是圆周角，并说明理由。
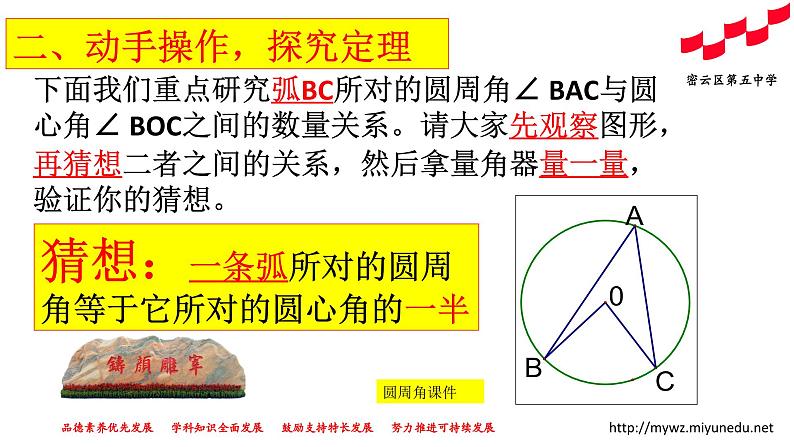
猜想：一条弧所对的圆周角等于它所对的圆心角的一半
下面我们重点研究弧BC所对的圆周角∠ BAC与圆心角∠ BOC之间的数量关系。请大家先观察图形，再猜想二者之间的关系，然后拿量角器量一量，验证你的猜想。
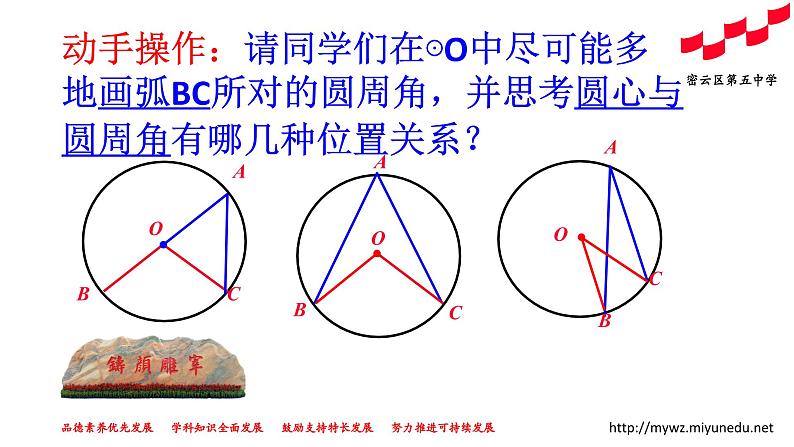
二、动手操作，探究定理
动手操作：请同学们在⊙O中尽可能多地画弧BC所对的圆周角，并思考圆心与圆周角有哪几种位置关系？
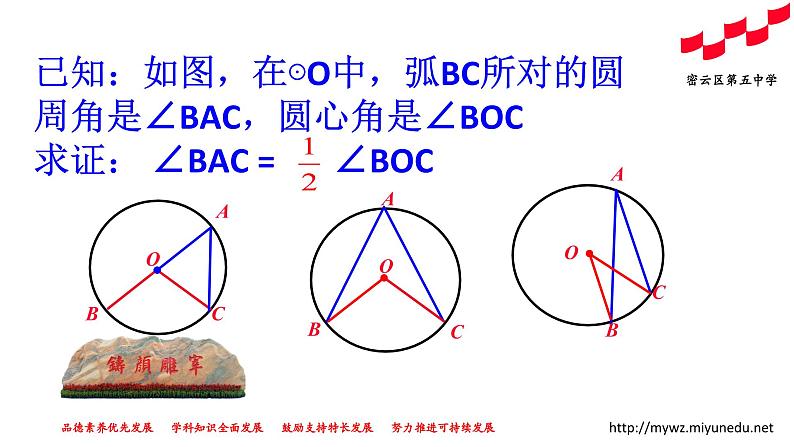
已知：如图，在⊙O中，弧BC所对的圆周角是∠BAC，圆心角是∠BOC求证： ∠BAC = ∠BOC
1.首先考虑一种特殊情况： 当圆心(O)在圆周角(∠BAC)的一边(BA)上时,圆周角∠BAC与圆心角∠BOC的大小关系.
又 ∠BOC=∠A＋∠C
你能证明第2种情况吗？
提示：作射线AO交⊙O于D 转化为第1种情况。
证明：由第1种情况得
你能证明第3种情况吗？
证明：作射线AO交⊙O于D。
一条弧所对的圆周角等于它所对的圆心角的一半。
辅助线：以圆周角的顶点为端点的直径
同弧或等弧所对的圆周角相等，在同圆或等圆中，相等的圆周角所对的弧也相等。
例题：如图，OA、OB、OC都是⊙O的半径，∠AOB = 2∠BOC. 求证：∠ACB = 2∠BAC.
1.试找出下图中所有相等的圆周角。
2、如图，在⊙O中∠ABC=50°，则∠AOC等于（ ）A、50°； B、80°；C、90°； D、100°
3、如图，△ABC是等边三角形，动点P在圆周的劣弧AB上，且不与A、B重合，则∠BPC等（ ）A、30°； B、60°；C、90°； D、45°
1、一条弧所对的圆周角的度数为60°,它所对的圆心角的度数为 _____ 2、一条弧所对的圆心角的度数为60°,它所对的圆周角的度数为 ______3、圆被弦分成1：3的两条弧,则这条弦所对的圆周角的度数 ___________4、已知OA,OB为⊙O的半径， ∠AOB=80° 点C在AB上， 则∠ACB = ______
注：同圆中一条弦对应两条弧，它所对的圆周角相等或互补。
A组：数学书第128页第1题的（1），（2）B组：数学书第128页第1题的（3）和 第4题C组：数学书第128页第3题和第6题