广东省揭阳市惠来县明德学校2022—2023学年下学期七年级期中数学试卷

这是一份广东省揭阳市惠来县明德学校2022—2023学年下学期七年级期中数学试卷，共11页。
A．a2•a3＝a6B．（a2）3＝a5C．（ab）2＝a2b2D．a6÷a3＝a2
2．（3分）随着电子技术的不断进步，电子元件的尺寸大幅度缩小，在芯片上某种电子元件大约只占有面积0.00000065mm2，0.00000065用科学记数法表示为（ ）
A．6.5×107B．6.5×10﹣6C．6.5×10﹣8D．6.5×10﹣7
3．（3分）一个三角形的三边长分别为4，7，x，那么x的取值范围是（ ）
A．3＜x＜11B．4＜x＜7C．﹣3＜x＜11D．x＞3
4．（3分）一副直角三角板如图放置（∠F＝∠ACB＝90°，∠E＝45°，∠A＝60°），如果点C在FD的延长线上，点B在DE上，且AB∥CF，则∠DBC的度数为（ ）
A．10°B．15°C．18°D．30°
5．（3分）如图，用三角板作△ABC的边AB上的高线，下列三角板的摆放位置正确的是（ ）
A．B．
C．D．
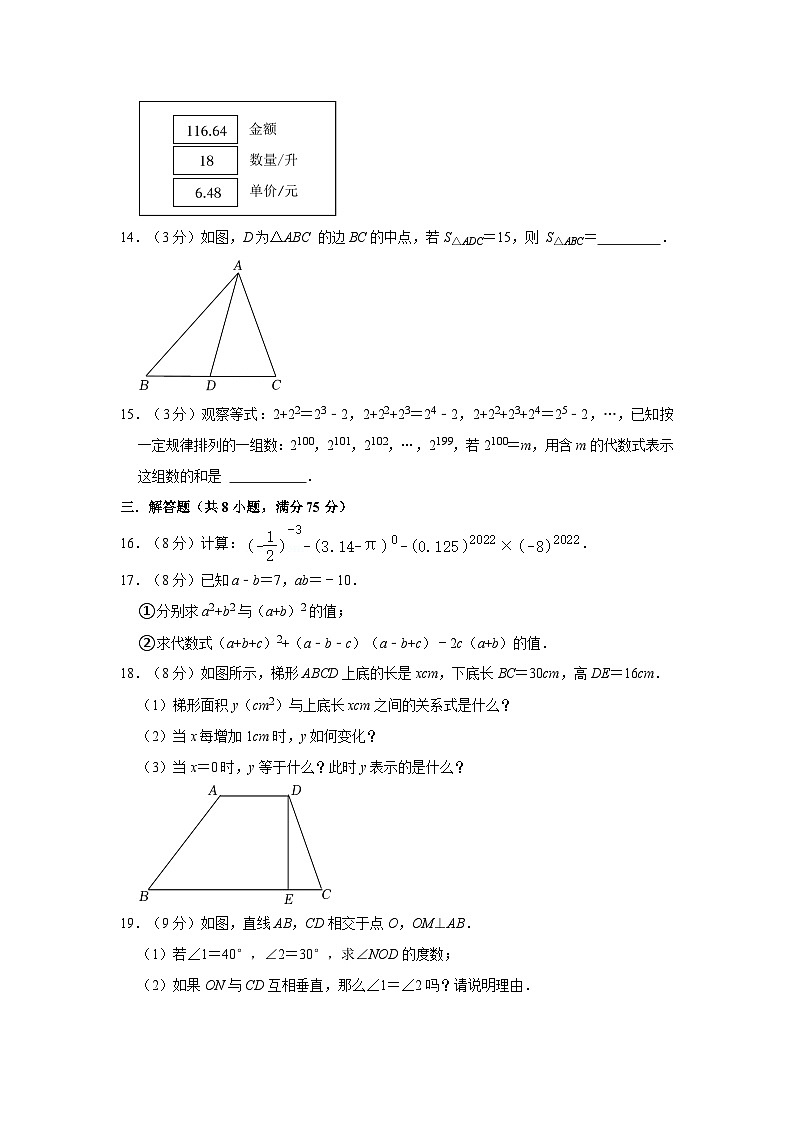
6．（3分）已知x2+2（m﹣1）x+9是一个完全平方式，则m的值为（ ）
A．4B．4或﹣2C．±4D．﹣2
7．（3分）设（5a+3b）2＝（5a﹣3b）2+A，则A等于（ ）
A．60abB．30abC．15abD．12ab
8．（3分）已知直线m∥n，将一块含30°角的直角三角板ABC按如图方式放置（∠ABC＝30°），其中A，B两点分别落在直线m，n上，若∠1＝15°，则∠2度数为（ ）
A．15°B．30°C．45°D．55°
9．（3分）画△ABC中AC边上的高，下列四个画法中正确的是（ ）
A．B．
C．D．
10．（3分）星期六早晨蕊蕊妈妈从家里出发去观山湖公园锻炼，她连续、匀速走了60min后回家，图中的折线段OA﹣AB﹣BC是她出发后所在位置离家的距离s（km）与行走时间t（min）之间的函数关系，则下列图形中可以大致描述蕊蕊妈妈行走的路线是（ ）
A．B．
C．D．
二．填空题（共5小题，满分15分，每小题3分）
11．（3分）运用乘法公式简便计算，862﹣85×87＝ ．
12．（3分）比较大小： ．（填“＞、＜、或＝”）
13．（3分）李师傅到单位附近的加油站加油，如图是所用的加油机上的数据显示牌，在金额、数量、单价三个量中，变量是 ．
14．（3分）如图，D为△ABC 的边BC的中点，若S△ADC＝15，则 S△ABC＝ ．
15．（3分）观察等式：2+22＝23﹣2，2+22+23＝24﹣2，2+22+23+24＝25﹣2，…，已知按一定规律排列的一组数：2100，2101，2102，…，2199，若2100＝m，用含m的代数式表示这组数的和是 ．
三．解答题（共8小题，满分75分）
16．（8分）计算：．
17．（8分）已知a﹣b＝7，ab＝﹣10．
①分别求a2+b2与（a+b）2的值；
②求代数式（a+b+c）2+（a﹣b﹣c）（a﹣b+c）﹣2c（a+b）的值．
18．（8分）如图所示，梯形ABCD上底的长是xcm，下底长BC＝30cm，高DE＝16cm．
（1）梯形面积y（cm2）与上底长xcm之间的关系式是什么？
（2）当x每增加1cm时，y如何变化？
（3）当x＝0时，y等于什么？此时y表示的是什么？
19．（9分）如图，直线AB，CD相交于点O，OM⊥AB．
（1）若∠1＝40°，∠2＝30°，求∠NOD的度数；
（2）如果ON与CD互相垂直，那么∠1＝∠2吗？请说明理由．
20．（9分）在日历上，我们可以发现其中某些数满足一定的规律，如图是2020年11月份的日历，我们任意用一个2×2的方框框出4个数，将其中4个位置上的数交叉相乘，再用较大的数减去较小的数，你发现了什么规律？
（1）图中方框框出的四个数，按照题目所说的计算规则，结果为 ．
（2）换一个位置试一下，是否有同样的规律？如果有，请你利用整式的运算对你发现的规律加以证明；如果没有，请说明理由．
21．（9分）已知多项式A＝x2+2x+n2，多项式B＝2x2+4x+3n2+3．
（1）若多项式x2+2x+n2是完全平方式，则n＝ ；
（2）有同学猜测B﹣2A的结果是定值，他的猜测是否正确，请说明理由；
（3）若多项式x2+2x+n2的值为﹣1，求x和n的值．
22．（12分）图a是一个长为2m、宽为2n的长方形，沿图中虚线用剪刀均分成四块小长方形，然后按图b的形状拼成一个正方形．
（1）你认为图b中的阴影部分的正方形的边长等于多少？
（2）请用两种不同的方法求图中阴影部分的面积．
方法1： ；
方法2： ．
（3）观察图b你能写出下列三个代数式之间的等量关系吗？
代数式：（m+n）2，（m﹣n）2，mn
（4）根据（3）题中的等量关系，解决如下问题：
若a+b＝7，ab＝5，则（a﹣b）2＝ ．（请直接写出计算结果）
23．（12分）【问题背景】同学们，我们一起观察小猪的猪蹄，你会发现一个我们熟悉的几何图形，我们就把这个图形象的称为“猪蹄模型”，猪蹄模型中蕴含着角的数量关系．
（1）如图①，AB∥CD，E为AB，CD之间一点，连接BE，DE，得到∠BED．试探究∠BED与∠B、∠D之间的数量关系，并说明理由．
（2）请你利用上述“猪蹄模型”得到的结论或解题方法，完成下面的问题：
【类比探究】如图②，AB∥CD，线段AD与线段BC相交于点E，∠BAD＝36°，∠BCD＝80°，EF平分∠BED交直线AB于点F，则∠BEF＝ °．
【拓展延伸】如图③，AB∥CD，线段AD与线段BC相交于点E，∠BAD＝36°，∠BCD＝80°，过点D作DG∥CB交直线AB于点G，AH平分∠BAD，DH平分∠CDG，则∠AHD＝ °．
2022-2023学年广东省揭阳市惠来县明德学校七年级（下）期中数学试卷
参考答案与试题解析
一．选择题（共10小题，满分30分，每小题3分）
1． 解：A、a2•a3＝a5，故A不符合题意；
B、（a2）3＝a6，故B不符合题意；
C、ab）2＝a2b2，故C符合题意；
D、a6÷a3＝a3，故D不符合题意；
故选：C．
2． 解：0.00000065＝6.5×10﹣7．
故选：D．
3． 解：∵三角形的三边长分别为4，7，x，
∴7﹣4＜x＜7+4，即3＜x＜11．
故选：A．
4． 解：∵∠F＝90°，∠E＝45°，
∴∠EDF＝45°，
∵∠ACB＝90°，∠A＝60°，
∴∠ABC＝30°，
∵AB∥CF，
∴∠ABD＝∠EDF＝45°，
∵∠ABC＝30°，
∴∠DBC＝∠ABD﹣∠ABC＝15°；
故选：B．
5． 解：A，C，D都不是△ABC的边AB上的高，
故选：B．
6． 解：∵x2+2（m﹣1）x+9是一个完全平方式，
∴2（m﹣1）＝±6，
解得：m＝4或m＝﹣2，
故选：B．
7． 解：∵（5a+3b）2＝（5a﹣3b）2+A，
∴A＝（5a+3b）2﹣（5a﹣3b）2
＝25a2+30ab+9b2﹣（25a2﹣30ab+9b2）
＝25a2+30ab+9b2﹣25a2+30ab﹣9b2
＝60ab．
故选：A．
8． 解：∵直线m∥n，
∴∠2＝∠ABC+∠1＝30°+15°＝45°，
故选：C．
9． 解：由三角形的高线的定义，C选项图形表示△ABC中AC边上的高．
故选：C．
10． 解：观察s关于t的函数图象，发现：
在图象AB段，该时间段蕊蕊妈妈离家的距离相等，即绕以家为圆心的圆弧进行运动，
∴可以大致描述蕊蕊妈妈行走的路线是B．
故选：B．
二．填空题（共5小题，满分15分，每小题3分）
11． 解：862﹣85×87＝862﹣（86+1）（86﹣1）＝862﹣（862﹣1）＝862﹣862+1＝1．
故答案为：1．
12． 解：∵（）2＝12，（3）2＝18，
而12＜18，
∴2＜3．
故答案为：＜．
13． 解：在金额、数量、单价三个量中，变量是金额、数量．
故答案为：金额、数量．
14． 解：设△ABC中BC边上的高为h，
∵S△ABD＝BD•h，S△ACD＝CD•h，D是△ABC的边BC的中点，
∴S△ADC＝S△ABD＝，
∵S△ADC＝15，
∴S△ABC＝2S△ACD＝30．
故答案为：30．
15． 解：由题意得：
2100+2101+2102+…+2199，
＝（2+22+23+…+2199）﹣（2+22+23+…+299），
＝（2200﹣2）﹣（2100﹣2），
＝（2100）2﹣2100，
＝m2﹣m，
故答案为：m2﹣m．
三．解答题（共8小题，满分75分）
16． 解：
＝（﹣2﹣1）﹣3﹣1﹣（0.125）2022×82022
＝﹣8﹣1﹣（0.125×8）2022
＝﹣8﹣1﹣1
＝﹣10．
17． 解：（1）当a﹣b＝7，ab＝﹣10时，
∵（a﹣b）2＝a2﹣2ab+b2，
∴72＝a2+b2﹣2×（﹣10），
∴a2+b2＝49﹣20＝29，
∵（a+b）2＝a2+b2+2ab，
∴（a+b）2＝29﹣2×（﹣10）＝49．
（2）原式＝[（a+b）+c]2+[（a﹣b）﹣c][（a﹣b）+c]﹣2c（a+b）
＝（a+b）2+2（a+b）c+c2+（a﹣b）2﹣c2﹣2c（a+b）
＝（a+b）2+（a﹣b）2
＝49+29
＝78．
18． 解：（1）y＝（x+30）×16
＝8x+240；
（2）当x每增加1cm时，y增加8cm2；
（3）当x＝0时，y等于240，此时y表示的是△ABC的面积．
19． 解：（1）∵OM⊥AB，
∴∠AOM＝90°，
∵∠1＝40°，
∴∠AOC＝∠AOM﹣∠1＝90°﹣40°＝50°，
∴∠NOD＝180°﹣∠AOC﹣∠2＝180°﹣50°﹣30°＝100°；
（2）∠1＝∠2，理由如下：
如果ON与CD互相垂直，
则∠CON＝90°，
∴∠COA+∠2＝90°，
∵OM⊥AB，
∴∠AOM＝90°，
∴∠COA+∠1＝90°，
∴∠1＝∠2．
20． 解：（1）10×4﹣3×11＝40﹣33＝7，
故答案为：7；
（2）设方框框出的四个数分别为a，a+1，a+7，a+8，
则（a+1）（a+7）﹣a（a+8）
＝a2+8a+7﹣a2﹣8a
＝7．
21． 解：（1）∵x2+2x+n2是一个完全平方式，
∴x2+2x+n2＝（x+1）2，
∴n2＝1，
∴n＝±1．
故答案为：±1；
（2）猜测不正确，理由：
∵A＝x2+2x+n2，B＝2x2+4x+3n2+3，
∴B﹣2A＝2x2+4x+3n2+3﹣2（x2+2x+n2）＝2x2+4x+3n2+3﹣2x2﹣4x﹣2n2＝n2+3，
∵结果含字母n，
∴B﹣2A的结果不是定值；
（3）由题意可得x2+2x+n2＝﹣1，
∴x2+2x+n2+1＝0，
∴（x+1）2+n2＝0，
∴x+1＝0，n＝0，
∴x＝﹣1．
22． 解：（1）图b中的阴影部分的正方形的边长等于长为m，宽为n的长方形的长宽之差，即m﹣n；
（2）方法一：图b中的阴影部分的正方形面积等于大正方形的面积减去4个长方形的面积，即（m+n）2﹣4mn；
方法二：图b中的阴影部分的正方形的边长等于m﹣n，所有其面积为（m﹣n）2；
故答案为（m+n）2﹣4mn，（m﹣n）2；
（3）（m﹣n）2＝（m+n）2﹣4mn；
（4）∵（a﹣b）2＝（a+b）2﹣4ab，
当a+b＝7，ab＝5，∴（a﹣b）2＝72﹣4×5＝29，
故答案为：29．
23． 解：（1）∠BED＝∠B+∠D，理由如下：
过E作ET∥AB，如图：
∵AB∥CD，
∴ET∥AB∥CD，
∴∠B＝∠BET，∠D＝∠DET，
∴∠B+∠D＝∠BET+∠DET，
即∠BED＝∠B+∠D；
（2）【类比探究】
同（1）方法可知：∠AEC＝∠BAD+∠BCD，
∵∠BAD＝36°，∠BCD＝80°，
∴∠AEC＝116°，
∴∠BED＝116°，
∵EF平分∠BED，
∴∠BEF＝∠BED＝58°，
故答案为：58；
【拓展延伸】
延长DH交AG于K，如图：
∵DG∥CB，
∴∠BCD+∠CDG＝180°，
∵∠BCD＝80°，
∴∠CDG＝100°，
∵DH平分∠CDG，
∴∠CDH＝∠CDG＝50°，
∵AB∥CD，
∴∠CDH+∠AKD＝180°，
∴∠AKD＝130°，
∵∠BAD＝36°，AH平分∠BAD，
∴∠KAH＝∠BAD＝18°，
∴∠AHK＝180°﹣∠KAH﹣∠AKH＝32°，
∴∠AHD＝180°﹣∠AHK＝148°，
故答案为：148．
声明：试题解析著作权属所有，未经书面同意，不得复制发布日期：2023/10/3 23:49:46；用户：王梓锋；邮箱：18813974184；学号：46897787