初中21.2.3 因式分解法精品导学案及答案

21.2.3因式分解法学案

【学习目标】

 1.知道如果，那么或.

 2.了解因式分解法的概念.

 3.会用因式分解法解某些一元二次方程．

 4.能根据具体的一元二次方程的特征，灵活选择方程的解法，体会解决问题方法的多样性.

【重点难点】

重点：会用提公因式法和运用乘法公式将整理成一般形式的方程左边因式分解．

难点：通过比较解一元二次方程的多种方法感悟因式分解法并能灵活应用.

【新知准备】

把下列各式因式分解

（1）10x-4.9x2； （2）2x(x-3)-5(x-3)；   （3）4y2-16；   （4）x2+12x+36；

【课堂探究】

一、自主探究

探究1

1. 若ab=0,则可以得到什么结论？

 2.试求下列方程的根 ：

 （1）x(x-5)=0;  （2）(x-1)(x+1)=0；   （3）(2x-1)(2x+1)=0；   （4）(2x-3)2=0.

探究2

    由上面你想到一元二次方程除了我们以前学的几种解法以外，还能转化成什么形式进

   行求解？

二、尝试应用

 1．解下列方程：

 （1）10x-4.9 x2 =0      （2）x（x-2）+x-2 =0       (3)5x2-2x-=x2-2x+

2. 选用合适方法解方程：

（1）x2+x-2=0；           （2）2x2-3=0；            （3）(x-2)2 =2-x；    

3. 用因式分解法解下列方程

 （1）x2+x=0                   （2）4x2-121=0      

（3）3x(2x+1)=4x+2             （4）(x-4)2=(5-2x)2

三、补偿提高

1. 已知（x+y）2 –x-y=0，求x+y的值．

2. 已知9a2-4b2=0，求代数式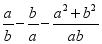的值．

【学后反思】

1. 通过本节课的学习你有那些收获?

2.还有那些疑惑？

21.2.3因式分解法学案答案

【新知准备】

（1）10x-4.9x2；                （2）2x(x-3)-5(x-3)； 

     =x（10-4.9x）                   =（x-3）（2x-5）

（3）4y2-16；                   （4）x2+12x+36；

     =（2y-4）（2y+4）              =

【课堂探究】

一、自主探究

1. a=0或b=0
2. （1）x1=0，x2=5 ;  （2）x1=1，x2=-1 ；   （3）x1=，x2=-；   （4）x1=x2=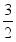

二、尝试应用

 1.（1）x1=0，x2= ;   （2）x1=2，x2=-1 ;   (3)x1=，x2=-；

2.（1））x1=1，x2=-2；   （2）x1= ，x2=-；   （3））x1=1，x2=2；  

 3.（1）x1=0，x2=-1 ; （2）x1=，x2=-; （3）x1=，x2=- ; （4）x1=1，x2=3;      

三、补偿提高

1.解：（x+y）2 –（x+y）=0

    （x+y）（x+y-1）=0

     x+y=0或x+y-1=0   ， 即 x+y=0或x+y=1

    2. 解：原式=

    ∵9a2-4b2=0

    ∴（3a+2b）（3a-2b）=0 

3a+2b=0或3a-2b=0，

a=-b或a=b

    当a=-b时，原式=-=3

    当a=b时，原式=-3．