-江苏省苏州市张家港市、常熟市等四市联考2020-2021学年八年级上学期期末数学试卷（word解析版）

这是一份-江苏省苏州市张家港市、常熟市等四市联考2020-2021学年八年级上学期期末数学试卷（word解析版），共31页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。

2020-2021学年江苏省苏州市张家港市、常熟市等四市联考八年级（上）期末数学试卷
一、选择题（本大题共10小题，每小题3分，共30分，在每小题给出的四个选项中，只有一项是符合题目要求的，把正确答案填在答题卡相应的位置上）
1．（3分）小篆，是在秦始皇统一六国后创制的汉字书写形式．下列四个小篆字中为轴对称图形的是（　　）
A． B． C． D．
2．（3分）下列四个实数、π、、中，无理数的个数有（　　）
A．1个 B．2个 C．3个 D．4个
3．（3分）如图，在平面直角坐标系中，被墨水污染部分遮住的点的坐标可能是（　　）

A．（3，2） B．（﹣3，2） C．（﹣3，﹣2） D．（3，﹣2）
4．（3分）在△ABC中，∠A、∠B、∠C的对边分别为a、b、c，下列条件不能判断△ABC是直角三角形的是（　　）
A．∠B＝∠C+∠A B．a2＝（b+c）（b﹣c）
C．∠A：∠B：∠C＝3：4：5 D．a：b：c＝3：4：5
5．（3分）在平面直角坐标系内，将点A（1，2）先向右平移2个单位长度，再向下平移1个单位长度，则平移后所得点的坐标是（　　）
A．（3，1） B．（3，3） C．（﹣1，1） D．（﹣1，3）
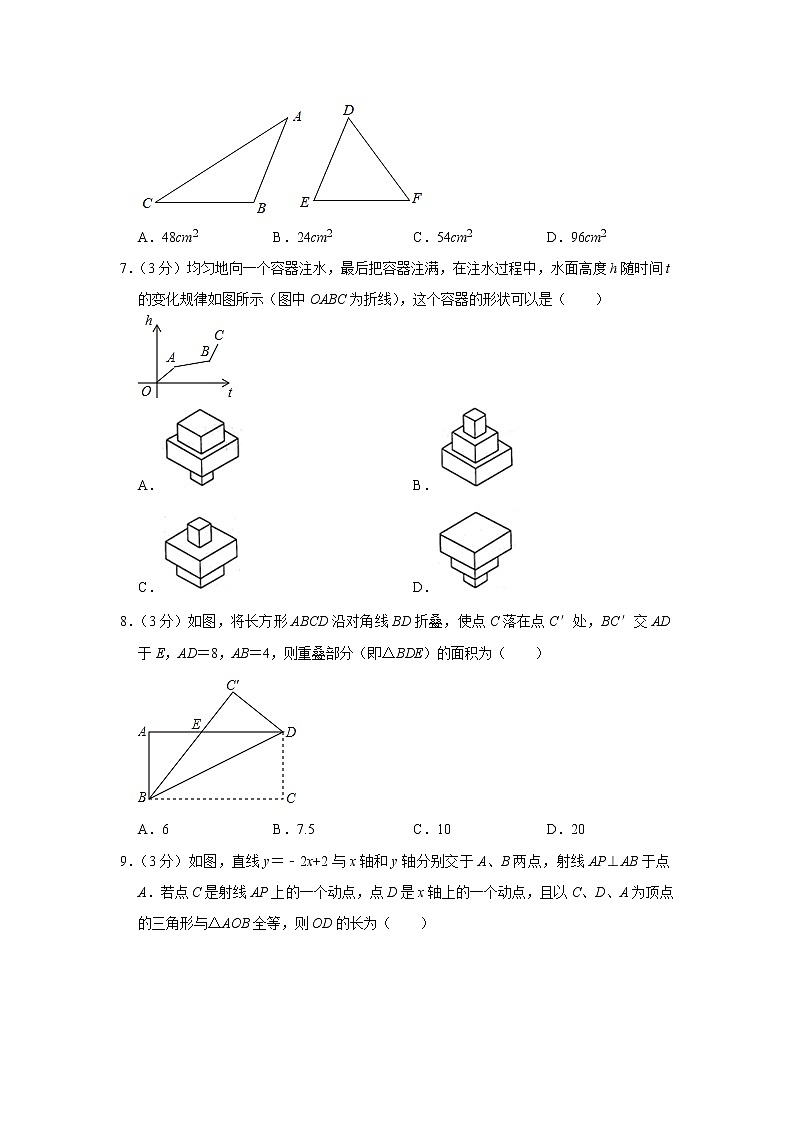
6．（3分）如图，在△ABC和△DEF中，AB＝DE，BC＝EF，∠B+∠E＝180°．如果△ABC的面积48cm2，那么△DEF的面积为（　　）

A．48cm2 B．24cm2 C．54cm2 D．96cm2
7．（3分）均匀地向一个容器注水，最后把容器注满，在注水过程中，水面高度h随时间t的变化规律如图所示（图中OABC为折线），这个容器的形状可以是（　　）

A． B．
C． D．
8．（3分）如图，将长方形ABCD沿对角线BD折叠，使点C落在点C′处，BC′交AD于E，AD＝8，AB＝4，则重叠部分（即△BDE）的面积为（　　）

A．6 B．7.5 C．10 D．20
9．（3分）如图，直线y＝﹣2x+2与x轴和y轴分别交于A、B两点，射线AP⊥AB于点A．若点C是射线AP上的一个动点，点D是x轴上的一个动点，且以C、D、A为顶点的三角形与△AOB全等，则OD的长为（　　）

A．2或+1 B．3或 C．2或 D．3或+1
10．（3分）如图，一次函数y＝2x和y＝ax+4的图象相交于点A（m，3），则不等式0＜ax+4＜2x的解集是（　　）

A．0＜x＜ B．＜x＜6 C．＜x＜4 D．0＜x＜3
二、填空题（本大题共8小题，每小题3分，共24分，请将答案填在答题卡相应的位置上）
11．（3分）若x3＝﹣1，则x＝　 　．
12．（3分）如图，△ABC≌△DEF，点B、F、C、E在同一条直线上，AC、DF交于点M，∠ACB＝43°，则∠AMF的度数是　 　°．

13．（3分）已知一次函数y＝x+b的图象经过点A（﹣1，1），则b的值是　 　．
14．（3分）一个三角形的三边的比是3：4：5，它的周长是36，则它的面积是　 　．
15．（3分）在平面直角坐标系内，已知点A（a+3，a）、B（a+7，a）关于y轴对称，则AB的长为　 　．
16．（3分）如图，在△ABC中，∠BAC＝105°，将△ABC绕点A逆时针旋转得到△AB′C′．若点B恰好落在BC边上，且AB′＝CB′，则∠C′的度数为　 　°．

17．（3分）如图，直线y＝﹣x+8与x轴、y轴分别交于点A、B，∠BAO的角平分线与y轴交于点M，则OM的长为　 　．

18．（3分）如图，在△ABC中，∠ACB＝90°，AC＝BC＝6cm，D是AB的中点，点E在AC上，过点D作DF⊥DE，交BC于点F．如果AE＝2cm，则四边形CEDF的周长是　 　cm．

三、解答题（本大题共76分.解答时应写出必要的计算或说明过程，并把解答过程填写在答题卡相应的位置上）
19．（5分）计算：（）2﹣﹣．
20．（6分）如图，点E、F在AB上，且AE＝BF，∠C＝∠D，AC∥BD．
求证：CF∥DE．

21．（6分）如图，在Rt△ABC中，∠C＝90°，AC＝8，AB＝10，AB的垂直平分线分别交AB、AC于点D、E．求AE的长．

22．（6分）已知点P（m，n）在一次函数y＝2x﹣3的图象上，且m＞2n，求m的取值范围．
23．（6分）如图，在平面直角坐标系中，A（﹣1，4），B（﹣3，3），C（﹣2，1）．
（1）已知△A1B1C1与△ABC关于x轴对称，画出△A1B1C1（请用2B铅笔将△A1B1C1描深）；
（2）在y轴上找一点P，使得△PBC的周长最小，试求点P的坐标．

24．（7分）如图，在△ABC中，AD是高，E、F分别是AB、AC的中点，AB＝8，
AC＝6．
（1）求四边形AEDF的周长；
（2）若∠BAC＝90°，求四边形AEDF的面积．

25．（8分）如图，已知直线l：y＝2x+b（b＞0）分别交x轴、y轴于点A、B．
（1）用含b的代数式表示点A的横坐标为　 　；
（2）如果△AOB的面积等于4，求b的值；
（3）如果直线l与一次函数y＝﹣2x﹣1和y＝x+2的图象交于同一点，求b的值．

26．（10分）如图，已知线段MN＝4，点A在线段MN上，且AM＝1，点B为线段AN上的一个动点．以A为中心顺时针旋转点M，以B为中心逆时针旋转点N，旋转角
分别为α和β．若旋转后M、N两点重合成一点C（即构成△ABC），设AB＝x．
（1）△ABC的周长为　 　；
（2）若α+β＝270°，求x的值；
（3）试探究△ABC是否可能为等腰三角形？若可能，求出x的值；若不可能，请说明理由．

27．（10分）如图，直线y＝4﹣x与两坐标轴分别相交于A、B两点，过线段AB上一点M分别作MC⊥OA于点C，MD⊥OB于点D，且四边形OCMD为正方形．

（1）正方形OCMD的边长为　 　．
（2）将正方形OCMD沿着x轴的正方向移动，得正方形EFGH，设平移的距离为a（0＜a≤4）．
①当平移距离a＝1时，正方形EFGH与△AOB重叠部分的面积为　 　；
②当平移距离a为多少时，正方形EFGH的面积被直线AB分成1：3两个部分？
28．（12分）某商店代理销售一种水果．某月30天的销售净利润（扣除每天需要缴纳各种费用50元后的利润）y（元）与销售量x（kg）之间函数关系的图象如图中折线所示．

日期
销售记录
1日
库存600kg，进价6元/kg，售价10元/kg（除了促销期间降价，其他时间售价保持不变）
9日
从1日起的9天内一共售出200kg
10、11日
这两天以进价促销，之后售价恢复到10元/kg
12日
补充进货200kg，进价6.5元/kg
30日
800kg水果全部售完，一共获利1200元
请根据图象及如表中销售记录提供的相关信息，解答下列问题：
（1）A点纵坐标m的值为　 　；
（2）求两天促销期间一共卖掉多少水果？
（3）求图象中线段BC所在直线对应的函数表达式．

2020-2021学年江苏省苏州市张家港市、常熟市等四市联考八年级（上）期末数学试卷
参考答案与试题解析
一、选择题（本大题共10小题，每小题3分，共30分，在每小题给出的四个选项中，只有一项是符合题目要求的，把正确答案填在答题卡相应的位置上）
1．（3分）小篆，是在秦始皇统一六国后创制的汉字书写形式．下列四个小篆字中为轴对称图形的是（　　）
A． B． C． D．
【分析】根据轴对称图形的概念判断即可．
【解答】解：A、本选项中小篆字不是轴对称图形，不符合题意；
B、本选项中小篆字不是轴对称图形，不符合题意；
C、本选项中小篆字不是轴对称图形，不符合题意；
D、本选项中小篆字是轴对称图形，符合题意；
故选：D．
【点评】本题考查的是轴对称图形的概念，轴对称图形的关键是寻找对称轴，图形两部分折叠后可重合．
2．（3分）下列四个实数、π、、中，无理数的个数有（　　）
A．1个 B．2个 C．3个 D．4个
【分析】根据无理数的概念求解即可．
【解答】解：＝3，
π，是无理数，共2个，
故选：B．
【点评】此题主要考查了无理数的定义，注意带根号的要开不尽方才是无理数，无限不循环小数为无理数．如π，，0.8080080008…（每两个8之间依次多1个0）等形式．
3．（3分）如图，在平面直角坐标系中，被墨水污染部分遮住的点的坐标可能是（　　）

A．（3，2） B．（﹣3，2） C．（﹣3，﹣2） D．（3，﹣2）
【分析】根据平面直角坐标系内各象限内点的坐标特点解答即可．
【解答】解：由图可知被墨水污染部分位于坐标系中第四象限，
所以被墨水污染部分遮住的点的坐标应位于第四象限，则可以为：（3，﹣2），
故选：D．
【点评】本题主要考查点的坐标，掌握平面直角坐标系内各象限内点的坐标特点是解题的关键．
4．（3分）在△ABC中，∠A、∠B、∠C的对边分别为a、b、c，下列条件不能判断△ABC是直角三角形的是（　　）
A．∠B＝∠C+∠A B．a2＝（b+c）（b﹣c）
C．∠A：∠B：∠C＝3：4：5 D．a：b：c＝3：4：5
【分析】利用直角三角形的定义和勾股定理的逆定理逐项判断即可．
【解答】解：A、∵∠B＝∠C+∠A，且∠A+∠B+∠C＝180°，∴∠B＝90°，故△ABC是直角三角形；
B、∵a2＝（b+c）（b﹣c），∴a2+c2＝b2，故△ABC是直角三角形；
C、∵∠A：∠B：∠C＝3：4：5，且∠A+∠B+∠C＝180°，∴最大角∠C＝75°≠90°，故△ABC不是直角三角形；
D、由条件可设a＝3k，则b＝4k，c＝5k，那么a2+b2＝c2，故△ABC是直角三角形；
故选：C．
【点评】本题考查了勾股定理的逆定理：如果三角形的三边长a，b，c满足a2+b2＝c2，那么这个三角形就是直角三角形．也考查了三角形内角和定理．
5．（3分）在平面直角坐标系内，将点A（1，2）先向右平移2个单位长度，再向下平移1个单位长度，则平移后所得点的坐标是（　　）
A．（3，1） B．（3，3） C．（﹣1，1） D．（﹣1，3）
【分析】根据平移的法则即可得出平移后所得点的坐标．
【解答】解：将点A（1，2）先向右平移2个单位长度，再向下平移1个单位长度，则平移后所得点的坐标是（1+2，2﹣1），
即（3，1），
故选：A．
【点评】本题考查了坐标与图形变化中的平移，根据根据平移的法则解答是解题的关键．
6．（3分）如图，在△ABC和△DEF中，AB＝DE，BC＝EF，∠B+∠E＝180°．如果△ABC的面积48cm2，那么△DEF的面积为（　　）

A．48cm2 B．24cm2 C．54cm2 D．96cm2
【分析】作AM⊥BC于M，DN⊥EF于N，如图，根据等角的余角相等得到∠ABM＝∠E，则可判断△ABM≌△DEN，所以AM＝DN，然后利用三角形的面积公式可得到S△DEF＝S△ABC．
【解答】解：作AM⊥BC于M，DN⊥EF于N，如图，
∵∠ABC+∠E＝180°，∠ABC+∠ABM＝180°，
∴∠ABM＝∠E，
在△ABM和△DEN中，
，
∴△ABM≌△DEN（AAS），
∴AM＝DN，
∵S△ABC＝•BC•AM，S△DEF＝•EF•DN，
而BC＝EF，
∴S△DEF＝S△ABC＝48cm2．
故选：A．

【点评】本题考查了三角形的面积：三角形的面积等于底边长与高线乘积的一半，即S△＝×底×高．也考查了全等三角形的判定与性质．
7．（3分）均匀地向一个容器注水，最后把容器注满，在注水过程中，水面高度h随时间t的变化规律如图所示（图中OABC为折线），这个容器的形状可以是（　　）

A． B．
C． D．
【分析】根据每一段函数图象的倾斜程度，反映了水面上升速度的快慢，再观察容器的粗细，作出判断．
【解答】解：注水量一定，从图中可以看出，OA上升较快，AB上升较慢，BC上升最快，
由此可知这个容器下面容积较大，中间容积最大，上面容积最小，
故选：C．
【点评】本题考查利用函数的图象解决实际问题，正确理解函数的图象所表示的意义是解题的关键，注意容器粗细和水面高度变化的关系．
8．（3分）如图，将长方形ABCD沿对角线BD折叠，使点C落在点C′处，BC′交AD于E，AD＝8，AB＝4，则重叠部分（即△BDE）的面积为（　　）

A．6 B．7.5 C．10 D．20
【分析】由折叠的性质和矩形的性质可证BE＝DE，设AE＝x，则BE＝DE＝8﹣x，在直角△ABE中利用勾股定理即可列方程求得x的值，然后根据三角形面积公式求解．
【解答】解：∵四边形ABCD是矩形，
∴AD∥BC，
∴∠EDB＝∠CBD，
由折叠的性质得：∠C'BD＝∠CBD，
∴∠EDB＝∠C'BD，
∴BE＝DE，
设AE＝x，则BE＝DE＝8﹣x，
在Rt△ABE中，AB2+AE2＝BE2，
即42+x2＝（8﹣x）2，
解得：x＝3，
则AE＝3，DE＝8﹣3＝5，
则S△BDE＝DE•AB＝×5×4＝10，
故选：C．
【点评】本题考查了折叠的性质、矩形的性质以及勾股定理，正确利用勾股定理求得AE的长是解决本题的关键．
9．（3分）如图，直线y＝﹣2x+2与x轴和y轴分别交于A、B两点，射线AP⊥AB于点A．若点C是射线AP上的一个动点，点D是x轴上的一个动点，且以C、D、A为顶点的三角形与△AOB全等，则OD的长为（　　）

A．2或+1 B．3或 C．2或 D．3或+1
【分析】根据题意解方程得到x＝0，则y＝2，令y＝0，则x＝1，求得OA＝1，OB＝2，根据勾股定理得到AB＝，①当∠ACD＝90°时，如图1，②当∠ADC＝90°时，如图2，根据全等三角形的性质即可得到结论．
【解答】解：∵AP⊥AB，
∴∠BAP＝∠AOB＝90°，
∴∠ABO+∠BAO＝∠CAD+∠BAO＝90°，
∴∠ABO＝∠CAD，
在y＝﹣2x+2中，
令x＝0，则y＝2，令y＝0，则x＝1，
∴OA＝1，OB＝2，由勾股定理得AB＝，
①当∠ACD＝90°时，如图1，
∵△AOB≌△DCA，
∴AD＝AB＝，
∴OD＝1+；
②当∠ADC＝90°时，如图2，
∵△AOB≌△CDA，
∴AD＝OB＝2，
∴OA+AD＝3，
综上所述：OD的长为1+或3．
故选：D．


【点评】本题考查了一次函数图像上点的坐标特征，待定系数法求函数的解析式，勾股定理的应用和全等三角形的性质等知识，分类讨论是解题关键，以防遗漏．
10．（3分）如图，一次函数y＝2x和y＝ax+4的图象相交于点A（m，3），则不等式0＜ax+4＜2x的解集是（　　）

A．0＜x＜ B．＜x＜6 C．＜x＜4 D．0＜x＜3
【分析】首先求得A的坐标，然后利用待定系数法求出y＝﹣x+4，再求得B的坐标，结合图象写出不等式0＜ax+4＜2x的解集即可．
【解答】解：∵函数y＝2x过点A（m，3），
∴2m＝3，
解得：m＝，
∴A（，3），
代入y＝ax+4得，3＝a+4，
∴a＝﹣，
∴y＝﹣x+4，
令y＝0，则x＝6，
∴B（6，0），
∴0＜ax+4＜2x的解集为＜x＜6．
故选：B．
【点评】此题主要考查了一次函数与一元一次不等式，关键是求出A、B点的坐标．
二、填空题（本大题共8小题，每小题3分，共24分，请将答案填在答题卡相应的位置上）
11．（3分）若x3＝﹣1，则x＝　﹣1　．
【分析】根据立方根的定义求解即可．
【解答】解：∵x3＝﹣1，
∴x＝＝﹣1，
故答案为：﹣1．
【点评】本题主要考查了立方根的定义，如果x3＝a，则称x是a的立方根，记作．
12．（3分）如图，△ABC≌△DEF，点B、F、C、E在同一条直线上，AC、DF交于点M，∠ACB＝43°，则∠AMF的度数是　86　°．

【分析】根据全等三角形的性质得到∠DFE＝∠ACB＝43°，根据三角形的外角性质计算，得到答案．
【解答】解：∵△ABC≌△DEF，
∴∠DFE＝∠ACB＝43°，
∵∠AMF是△MFC的一个外角，
∴∠AMF＝∠DFE+∠ACB＝86°，
故答案为：86．
【点评】本题考查的是全等三角形的性质、三角形的外角性质，掌握全等三角形的对应角相等是解题的关键．
13．（3分）已知一次函数y＝x+b的图象经过点A（﹣1，1），则b的值是　2　．
【分析】把点A的坐标代入函数解析式进行计算即可．
【解答】解：∵一次函数y＝x+b的图象经过点A（﹣1，1），
∴1＝﹣1+b，
解得：b＝2，
故答案为：2．
【点评】此题主要考查了一次函数图象上点的坐标特点，关键是掌握函数图象经过的点必能满足解析式．
14．（3分）一个三角形的三边的比是3：4：5，它的周长是36，则它的面积是　54　．
【分析】根据勾股定理的逆定理得到三角形是直角三角形，然后根据三角形的面积公式即可得到结论．
【解答】解：设三角形的三边是3x：4x：5x，
∵（3x）2+（4x）2＝（5x）2，
∴此三角形是直角三角形，
∵它的周长是36，
∴3x+4x+5x＝36，
∴3x＝9，4x＝12，
∴三角形的面积＝×9×12＝54，
故答案为：54．
【点评】本题考查了勾股定理的逆定理，三角形的面积的计算，熟练掌握勾股定理的逆定理是解题的关键．
15．（3分）在平面直角坐标系内，已知点A（a+3，a）、B（a+7，a）关于y轴对称，则AB的长为　4　．
【分析】直接利用关于y轴对称点的性质得出a的值，进而得出答案．
【解答】解：∵点A（a+3，a）、B（a+7，a）关于y轴对称，
∴a+3+a+7＝0，
解得：a＝﹣5，
故a+3＝﹣2，a+7＝2，
则AB的长为：4．
故答案为：4．
【点评】此题主要考查了关于y轴对称点的性质，正确得出关于y轴对称点横纵坐标的关系是解题关键．
16．（3分）如图，在△ABC中，∠BAC＝105°，将△ABC绕点A逆时针旋转得到△AB′C′．若点B恰好落在BC边上，且AB′＝CB′，则∠C′的度数为　25　°．

【分析】由三角形的内角和定理可得∠B+∠C＝75°，由等腰三角形的性质和旋转的性质可得∠B＝∠AB'B＝2∠C，即可求解．
【解答】解：∵∠BAC＝105°，
∴∠B+∠C＝75°，
∵AB′＝CB′，
∴∠C＝∠CAB'，
∴∠AB'B＝∠C+∠CAB'＝2∠C，
∵将△ABC绕点A逆时针旋转得到△AB′C′，
∴AB＝AB'，
∴∠B＝∠AB'B＝2∠C，
∴∠C＝25°，
故答案为：25．
【点评】本题考查了旋转的性质，等腰三角形的性质，掌握旋转的性质是解题的关键．
17．（3分）如图，直线y＝﹣x+8与x轴、y轴分别交于点A、B，∠BAO的角平分线与y轴交于点M，则OM的长为　3　．

【分析】过M点作MN⊥AB于N，如图，先利用坐标轴上点的坐标特征求出A、B点的坐标，则可计算出AB＝10，再利用角平分线的性质得MO＝MN，然后利用面积法得到×6•OM+×10•MN＝×6×8，从而可求出OM的长．
【解答】解：过M点作MN⊥AB于N，如图，
当y＝0时，﹣x+8＝0，解得x＝6，则A（6，0）；
当x＝0时，y＝﹣x+8＝8，则B（0，8），
∴AB＝＝10，
∵AM平分∠OAB，
∴MO＝MN，
∵S△OMA+S△BMA＝S△OAB，
∴×6•OM+×10•MN＝×6×8，
即3OM+5MN＝24，
∴8OM＝24，
∴OM＝3．
故答案为3．

【点评】本题考查了一次函数图象上点的坐标特征：一次函数图象上点的坐标满足其解析式．也考查了一次函数的性质．
18．（3分）如图，在△ABC中，∠ACB＝90°，AC＝BC＝6cm，D是AB的中点，点E在AC上，过点D作DF⊥DE，交BC于点F．如果AE＝2cm，则四边形CEDF的周长是　（6+2）　cm．

【分析】连接CD，EF，根据AAS证明△AED≌△CFD，再根据勾股定理可得EF的长，由△DEF是等腰直角三角形，即可解决问题．
【解答】解：如图，连接CD，EF，

∵∠ACB＝90°，AC＝BC，
∴∠A＝45°，
∵D是AB的中点，
∴CD＝AB＝AD．
∴∠DCA＝∠A＝∠DCB＝45°，
∵DF⊥DE，
∴∠EDF＝90°，
∴∠DEF+∠DFC＝180°，
∵∠AED+∠DEF＝180°，
∴∠AED＝∠DFC，
在△AED和△CFD中，
，
∴△AED≌△CFD（AAS），
∴DE＝DF，AE＝CF＝2cm，
∴CE＝AC﹣AE＝6﹣2＝4（cm），
∴EF＝＝＝2（cm），
∵△DEF是等腰直角三角形，
∴DE2+DF2＝EF2，
∴2DE2＝EF2，
∴DE＝DF＝EF＝，
∴四边形CEDF的周长是CE+CF+DE+DF＝CE+AE+2DE＝AC+2DE＝（6+2）cm．
故答案为：（6+2）．
【点评】本题考查了全等三角形的判定与性质，等腰直角三角形的性质，勾股定理，解决本题的关键是掌握全等三角形的判定与性质．
三、解答题（本大题共76分.解答时应写出必要的计算或说明过程，并把解答过程填写在答题卡相应的位置上）
19．（5分）计算：（）2﹣﹣．
【分析】原式利用平方根及立方根定义化简，计算即可得到结果．
【解答】解：原式＝3﹣（﹣4）﹣5
＝3+4﹣5
＝2．
【点评】此题考查了实数的运算，熟练掌握运算法则是解本题的关键．
20．（6分）如图，点E、F在AB上，且AE＝BF，∠C＝∠D，AC∥BD．
求证：CF∥DE．

【分析】根据已知条件证明△ACF≌△BDE可得∠AFC＝∠BED，进而可得CF∥DE．
【解答】证明：∵AE＝BF，
∴AE+EF＝BF+EF，
即AF＝BE，
∵AC∥BD，
∴∠A＝∠B，
在△ACF和△BDE中，
，
∴△ACF≌△BDE（AAS），
∴∠AFC＝∠BED，
∴CF∥DE．
【点评】本题考查了全等三角形的判定与性质，解决本题的关键是掌握全等三角形的判定与性质．
21．（6分）如图，在Rt△ABC中，∠C＝90°，AC＝8，AB＝10，AB的垂直平分线分别交AB、AC于点D、E．求AE的长．

【分析】由勾股定理先求出BC＝6，连接BE，根据中垂线的性质设AE＝BE＝x，知CE＝8﹣x，在Rt△BCE中由BC2+CE2＝BE2列出关于x的方程，解之可得答案．
【解答】解：在Rt△ABC中，∠C＝90°，AC＝8，AB＝10，
∴BC＝＝＝6，
连接BE，

∵DE垂直平分AB，
∴AE＝BE，
设AE＝BE＝x，则CE＝8﹣x，
在Rt△BCE中，∵BC2+CE2＝BE2，
∴62+（8﹣x）2＝x2，
解得x＝，
∴AE＝．
【点评】本题主要考查勾股定理，解题的关键是掌握勾股定理及线段中垂线的性质．
22．（6分）已知点P（m，n）在一次函数y＝2x﹣3的图象上，且m＞2n，求m的取值范围．
【分析】先由点P（m，n）在一次函数y＝2x﹣3的图象上知n＝2m﹣3，将其代入m＞2n，进一步求解即可．
【解答】解：∵点P（m，n）在一次函数y＝2x﹣3的图象上，
∴n＝2m﹣3，
∵m＞2n，
∴m＞2（2m﹣3），
解得m＜2．
【点评】本题主要考查一次函数图象上点的坐标特征，解题的关键是掌握一次函数图象上点的坐标满足一次函数的解析式．
23．（6分）如图，在平面直角坐标系中，A（﹣1，4），B（﹣3，3），C（﹣2，1）．
（1）已知△A1B1C1与△ABC关于x轴对称，画出△A1B1C1（请用2B铅笔将△A1B1C1描深）；
（2）在y轴上找一点P，使得△PBC的周长最小，试求点P的坐标．

【分析】（1）分别作出三个顶点关于x轴的对称点，再首尾顺次连接即可；
（2）作点C关于y轴的对称点C′，利用待定系数法求BC′所在直线解析式，再求出x＝0时y的值即可．
【解答】解：（1）如图所示，△A1B1C1即为所求．

（2）如图所示，点P即为所求，
点C关于y轴的对称点C′（2，1），
设BC′所在直线解析式为y＝kx+b，
则，
解得，
∴BC′所在直线解析式为﹣x+，
当x＝0时，y＝，
所以点P坐标为（0，）．
【点评】本题主要考查作图﹣轴对称变换，解题的关键是掌握轴对称变换的定义和性质，并据此得出变换后的对称点及待定系数法求直线解析式．
24．（7分）如图，在△ABC中，AD是高，E、F分别是AB、AC的中点，AB＝8，
AC＝6．
（1）求四边形AEDF的周长；
（2）若∠BAC＝90°，求四边形AEDF的面积．

【分析】（1）根据直角三角形的性质得到DE＝AB＝4，DF＝AC＝3，根据四边形的周长公式计算，得到答案；
（2）根据三角形的面积公式计算即可．
【解答】解：（1）∵AD是△ABC的高，
∴∠ADB＝∠ADC＝90°，
∵E、F分别是AB、AC的中点，AB＝8，AC＝6，
∴DE＝AB＝4，DF＝AC＝3，AE＝4，AF＝3，
∴四边形AEDF的周长＝AE+DE+DF+AF＝14；
（2）△ABC的面积＝×AB×AC＝24，
∵E、F分别是AB、AC的中点，
∴△ADE的面积＝△BDE的面积，△ADF的面积＝△CDF的面积，
∴四边形AEDF的面积＝×△ABC的面积＝12．
【点评】本题考查的是直角三角形的性质，掌握在直角三角形中，斜边上的中线等于斜边的一半是解题的关键．
25．（8分）如图，已知直线l：y＝2x+b（b＞0）分别交x轴、y轴于点A、B．
（1）用含b的代数式表示点A的横坐标为　﹣　；
（2）如果△AOB的面积等于4，求b的值；
（3）如果直线l与一次函数y＝﹣2x﹣1和y＝x+2的图象交于同一点，求b的值．

【分析】（1）令y＝0，求得x的值即可；
（2）求得B的坐标，根据题意得到OA•OB＝4，即＝4，即可求得b＝4；
（3）求得一次函数y＝﹣2x﹣1和y＝x+2的图象的交点，代入直线l的解析式即可求得．
【解答】解：（1）∵直线l：y＝2x+b（b＞0）分别交x轴、y轴于点A、B．
∴令y＝0，则0＝2x+b，解得x＝﹣，
∴点A的横坐标为﹣，
故答案为﹣；
（2）令x＝0，则y＝b，
∴B（0，b），
∵△AOB的面积等于4，
∴OA•OB＝4，即＝4，
解得b＝4；
（2）由解得，
∴直线l与一次函数y＝﹣2x﹣1和y＝x+2的图象交于同一点（﹣1，1），
把（﹣1，1）代入y＝2x+b（b＞0）得，1＝﹣2+b，
∴b＝3．
【点评】本题是两条直线相交或平行问题，考查了一次函数图像上点的坐标特征，两条直线交点的求法，三角形的面积等，求得交点坐标是解题的关键．
26．（10分）如图，已知线段MN＝4，点A在线段MN上，且AM＝1，点B为线段AN上的一个动点．以A为中心顺时针旋转点M，以B为中心逆时针旋转点N，旋转角
分别为α和β．若旋转后M、N两点重合成一点C（即构成△ABC），设AB＝x．
（1）△ABC的周长为　4　；
（2）若α+β＝270°，求x的值；
（3）试探究△ABC是否可能为等腰三角形？若可能，求出x的值；若不可能，请说明理由．

【分析】（1）由旋转的性质得出AC＝AM，BC＝BN，则可得出答案；
（2）求出∠ACB＝90°，由勾股定理可得出答案；
（3）分三种情况讨论，当AC＝BC＝1时，当AB＝AC＝1时，当BC＝BA时，由三角形三边关系及等腰三角形的性质可得出答案．
【解答】解：（1）∵以A为中心顺时针旋转点M，以B为中心逆时针旋转点N，
∴AC＝AM，BC＝BN，
∵MN＝4，
∴△ABC的周长＝AC+AB+BC＝AM+AB+BN＝MN＝4．
故答案为：4；
（2）∵∠MAC＝α，∠NBC＝β，α+β＝270°，
∴∠MAC+∠NBC＝270°，
∴∠CAB+∠CBA＝360°﹣270°＝90°，
∴∠ACB＝90°，
∵AM＝1，AB＝x，MN＝4，
∴AC＝1，BC＝BN＝（3﹣x），
由勾股定理得，12+（3﹣x）2＝x2，
解得x＝；
（3）存在，理由如下：
∵AC＝1，△ABC为等腰三角形，
∴当AC＝BC＝1时，则AB＝2，
此时1+1＝2，△ABC不存在，舍去，
当AB＝AC＝1时，同理，不合题意舍去，
当BC＝AB时，
∵AC＝1，AB+AC+BC＝4，
∴AB+BC＝3，
∴AB＝BC＝，
此时1+，符合题意，
∴△ABC能为等腰三角形，AB＝x＝．
【点评】本题是几何变换综合题，考查了旋转的性质，勾股定理，等腰三角形的判定与性质，三角形三边关系，三角形的周长，熟练掌握旋转的性质是解题的关键．
27．（10分）如图，直线y＝4﹣x与两坐标轴分别相交于A、B两点，过线段AB上一点M分别作MC⊥OA于点C，MD⊥OB于点D，且四边形OCMD为正方形．

（1）正方形OCMD的边长为　2　．
（2）将正方形OCMD沿着x轴的正方向移动，得正方形EFGH，设平移的距离为a（0＜a≤4）．
①当平移距离a＝1时，正方形EFGH与△AOB重叠部分的面积为　　；
②当平移距离a为多少时，正方形EFGH的面积被直线AB分成1：3两个部分？
【分析】（1）设点M（x，4﹣x），由正方形的性质可得OC＝CM，即可求解；
（2）①先求出S△MEQ＝EM2＝，即可求解；
②分两种情况讨论，由等腰直角三角形的性质和正方形的性质可求解．
【解答】解：（1）设点M（x，4﹣x），
∵当四边形OCMD为正方形时，OC＝CM，即x＝4﹣x，
∴x＝2，
∴CM＝OC＝2，
故答案为2；
（2）①∵直线AB的解析式为y＝﹣x+4，
∴移动过程中正方形EFGH被分割出的三角形是等腰直角三角形，
如图1，

∵四边形EFGH是正方形，
∴正方形EFGH的面积＝22＝4，
当a＝1时，EM＝1，
∴S△MQE＝EM2＝，
∴正方形EFGH与△AOB重叠部分的面积＝4﹣＝；
故答案为；
②∵正方形EFGH的面积被直线AB分成1：3两个部分，
∴两部分的面积分别为1和3．
当0＜a≤2时，如图2所示：

∵直线AB的解析式为y＝4﹣x，
∴∠BAO＝45°，
∴△MQE为等腰直角三角形，
∴EQ＝ME，
∴ME2＝1，
∴ME＝，即a＝，
当2＜a＜4时，如图3所示：

∵∠BAO＝45°，
∴△AGQ为等腰直角三角形．
∴GQ＝GA．
∴GA2＝1，解得：GA＝．
∵将y＝0代入y＝4﹣x得：4﹣x＝0，
∴x＝4，
∴OA＝4．
∴OG＝4﹣，即a＝4﹣．
综上所述，当平移的距离为a＝或a＝4﹣时，正方形EFGH的面积被直线AB分成1：3两个部分．
【点评】本题是一次函数综合题，考查的是一次函数的综合应用，解答本题主要应用了﹣﹣﹣函数图象的点的坐标与函数解析式的关系，正方形的性质，等腰直角三角形的性质和判定，证得△MQE、△GQA是等腰直角三角形是解题的关键．
28．（12分）某商店代理销售一种水果．某月30天的销售净利润（扣除每天需要缴纳各种费用50元后的利润）y（元）与销售量x（kg）之间函数关系的图象如图中折线所示．

日期
销售记录
1日
库存600kg，进价6元/kg，售价10元/kg（除了促销期间降价，其他时间售价保持不变）
9日
从1日起的9天内一共售出200kg
10、11日
这两天以进价促销，之后售价恢复到10元/kg
12日
补充进货200kg，进价6.5元/kg
30日
800kg水果全部售完，一共获利1200元
请根据图象及如表中销售记录提供的相关信息，解答下列问题：
（1）A点纵坐标m的值为　350　；
（2）求两天促销期间一共卖掉多少水果？
（3）求图象中线段BC所在直线对应的函数表达式．
【分析】（1）由表格信息可知，从6月1日到6月9日，成本价6元/kg，售价10元/kg，一共售出200kg，根据利润＝每千克的利润×销售量列式计算即可；
（2）由题意得出方程，解方程即可；
（3）先求出点B的坐标，再由待定系数法求解即可．
【解答】解：∵从1日起的9天内一共售出200kg，
∴总利润为200（10﹣6）﹣9×50＝350（元），
故答案为：350；
（2）设促销期间一共卖掉xkg水果，
本月总成本为：600×6+200×6.5+50×30＝6400（元），
本月总售价为：200×10+x•6+（800﹣200﹣x）•10＝（8000﹣4x）元，
由图象可知本月总利润为1200元，
∴8000﹣4x﹣6400＝1200，
解得：x＝100，
即两天促销期间一共卖掉100kg水果；
（3）由（2）可知两天促销期间一共卖掉100kg水果，
∴B的横坐标200+100＝300，
∴两天促销期间的净利润为
100（6﹣6）﹣2×50＝﹣100（元），
∴点B的纵坐标为350﹣100＝250，
∴B（300，250），
设直线BC的解析式为y＝kx+b，
把点B（300，250）和C（800，1200）的坐标代入得：，
解得：，
∴图象中线段BC所在直线对应的函数表达式为y＝x﹣320．
【点评】本题考查了一次函数的应用、待定系数法以及二元一次方程组的应用等知识；熟练掌握一次函数的应用和待定系数法是解题的关键．