高中数学人教A版 (2019)必修 第一册第二章 一元二次函数、方程和不等式2.3 二次函数与一元二次方程、不等式示范课课件ppt

这是一份高中数学人教A版 (2019)必修 第一册第二章 一元二次函数、方程和不等式2.3 二次函数与一元二次方程、不等式示范课课件ppt，共29页。PPT课件主要包含了自主学习，一元二次，经典例题，当堂达标等内容，欢迎下载使用。

1、了解一元二次不等式的概念；2、掌握一元二次不等式的解法；3、理解三个二次的关系，能够利用这种关系解题；4、掌握与一元二次不等式有关的恒成立问题的解法.
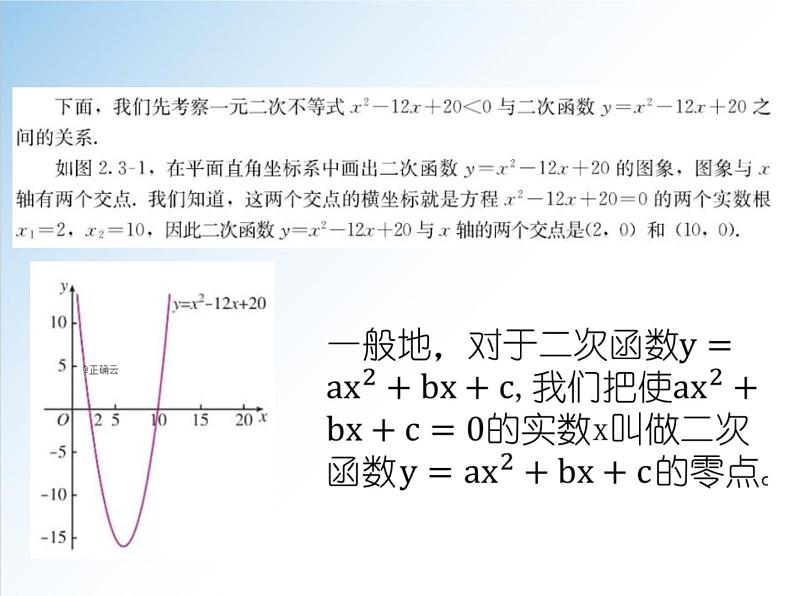
在初中，我们从一次函数的角度看一元一次方程、一元一次不等式，发现了三者之间的内在联系，利用这种联系可以更好的解决相关问题。对于二次函数、一元二次方程和一元二次不等式，是否也有这样的联系呢？
知识点一　一元二次不等式的概念(1)只含有一个未知数，并且未知数的最高次数是2的不等式，称为 不等式.(2)能使不等式成立的未知数x的一个值称为不等式的一个解.(3)不等式所有解的 称为解集.
知识点二　一元二次不等式的解法解一元二次不等式的步骤：(1)化为基本形式ax2＋bx＋c>0或ax2＋bx＋c<0(其中a>0)；(2)计算Δ＝b2－4ac，以确定一元二次方程ax2＋bx＋c＝0是否有解；(3)有根求根；(4)根据图象写出不等式的解集.
知识点三　“三个二次”的关系一元二次不等式与相应的一元二次方程、二次函数的联系，如下表.
1.x2＞1的一个解是x＝－2，解集是(－∞，－1)∪(1，＋∞).(　　)2.方程x2－1＝0相当于函数y＝x2－1中y＝0.(　　)3.如果关于x的方程ax2＋bx＋c＝0无解，则不等式ax2＋bx＋c>0也无解.(　　)4.x2－1>0与1－x2<0的解集相等.(　　)
题型一 一元二次不等式的解法
总结：用框图表示一元二次不等式的求解过程
跟踪训练1　（1）求不等式2x2－3x－2≥0的解集.
（2）求不等式－3x2＋6x>2的解集.
解　不等式可化为3x2－6x＋2<0，∵Δ＝(－6)2－4×3×2＝12>0，
∴不等式－3x2＋6x>2的解集是
题型二　含参数的一元二次不等式的解集
例4　已知关于x的不等式x2＋ax＋b<0的解集为{x|10的解集.
∴不等式bx2＋ax＋1>0，即2x2－3x＋1>0.
总结：　给出一元二次不等式的解集，相当于知道了相应二次函数的开口方向及与x轴的交点，可以利用代入根或根与系数的关系求待定系数.
跟踪训练 2　已知不等式ax2－bx＋2<0的解集为{x|1解　方法一　由题设条件知a>0，且1,2是方程ax2－bx＋2＝0的两实根.
方法二　把x＝1,2分别代入方程ax2－bx＋2＝0中，
题型三　不等式恒成立问题
例5　设函数f(x)＝mx2－mx－1.若对于一切实数x，f(x)<0恒成立，求实数m的取值范围。
解　要使mx2－mx－1<0恒成立，若m＝0，显然－1<0，满足题意；
跟踪训练 3 若不等式x2＋x＋k<0在区间[－1,1]上恒成立，则实数k的取值范围是 .
解析　x2＋x＋k<0，即k<－(x2＋x)在区间[－1,1]上恒成立，即k<[－(x2＋x)]min.当x＝1时，[－(x2＋x)]min＝－2.∴k<－2.
1.不等式2x2－x－1>0的解集是
解析　∵2x2－x－1＝(2x＋1)(x－1)，∴由2x2－x－1>0，得(2x＋1)(x－1)>0，
2.若不等式x2＋mx＋1≥0的解集为R，则实数m的取值范围是A.m≥2 B.m≤－2C.m≤－2或m≥2 D.－2≤m≤2
解析　由题意，得Δ＝m2－4≤0，∴－2≤m≤2.
3.不等式(x－2)2<－2x＋11的解集为 .
解析　不等式(x－2)2<－2x＋11可化为(x－1)2<8，
4.若不等式ax2＋8ax＋21<0的解集是{x|－7解析　由题意可知－7和－1为方程ax2＋8ax＋21＝0的两个根.
1.解一元二次不等式的常见方法(1)图象法：由一元二次方程、一元二次不等式及二次函数的关系，可以得到解一元二次不等式的一般步骤：①化不等式为标准形式：ax2＋bx＋c>0(a>0)或ax2＋bx＋c<0(a>0)；②求方程ax2＋bx＋c＝0(a>0)的根，并画出对应函数y＝ax2＋bx＋c图象的简图；③由图象得出不等式的解集.(2)代数法：将所给不等式化为一般式后借助分解因式或配方求解.当m0，则可得{x|x>n或x2.实际问题要注意变量的实际含义对变量范围的影响，如长度应该大于0，人数应该为自然数等.3.由一元二次不等式的解集可以逆推二次函数的开口及与x轴的交点坐标.