

2021年陕西省西安市长安区中考数学一模试卷(word版 含答案)
展开2021年陕西省西安市长安区中考数学一模试卷
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.比﹣5小3的数是( )
A.﹣2 B.2 C.﹣8 D.8
2.根据“头条”报道,2021年大年初一,长安区樊川公园当日客流量突破30万人,30万用科学记数法表示正确的是( )
A.0.3×106 B.3×106 C.3×105 D.30×104
3.下列计算正确的是( )
A.a2+a3=a5 B.(-2x2y)3=-6x6y3
C.(a-b)(-a-b)=a2-b2 D.2x2(-xy)=-x3y
4.如图,AB∥EF,∠B=75°,∠FDC=135°,则∠C的度数等于( )
A.30° B.35° C.45° D.60°
5.已知,正比例函数y=kx的图象经过点(a,b),且=2,则k的值等于( )
A. B.2 C.﹣2 D.﹣
6.如图,在△ABC中,AD⊥BC于点D,且BD=CD,若△ABD的中线BF=2,则AC的长为( )
A.5 B.4 C.3 D.2
7.已知直线l1过点(﹣1,0),直线l2过点(0,2),且l1和l2关于直线x=1对称,则直线l1和l2的交点坐标为( )
A.(1,) B.(1,) C.(1,) D.(1,)
8.如图,在正方形ABCD中,AB=4.E,F分别为边AB,BC的中点,连接AF,DE,点N,M分别为AF,DE的中点,连接MN,则MN的长为( )
A. B.2 C. D.2
9.如图,在以AB为直径的半⊙O中,=,点D为上一点,连接OC,BD交于点E,连接OD,若∠DEC=65°,则∠DOC的度数等于( )
A.25° B.32.5° C.35° D.40°
10.已知,抛物线y=ax2+2ax在其对称轴的左侧y随x的增大而减小,关于x的方程ax2+2ax=m(m>0)的一个根为﹣4,而关于x的方程ax2+2ax=n(0<n<m)有两个整数根,则这两个根的积是( )
A.0 B.﹣3 C.﹣6 D.﹣8
二、填空题
11.实数a在数轴上对应点的位置如图所示,若实数b满足﹣a<b<a,则b的值可以是___(任填一个即可).
12.如图所示的六边形花环是用六个全等的直角三角形拼成的,则等于_______度.
13.在平面直角坐标系中,直线y=﹣x与双曲线y=﹣交于点A(x1,y1),B(x2,y2),则x1﹣y2的值为___.
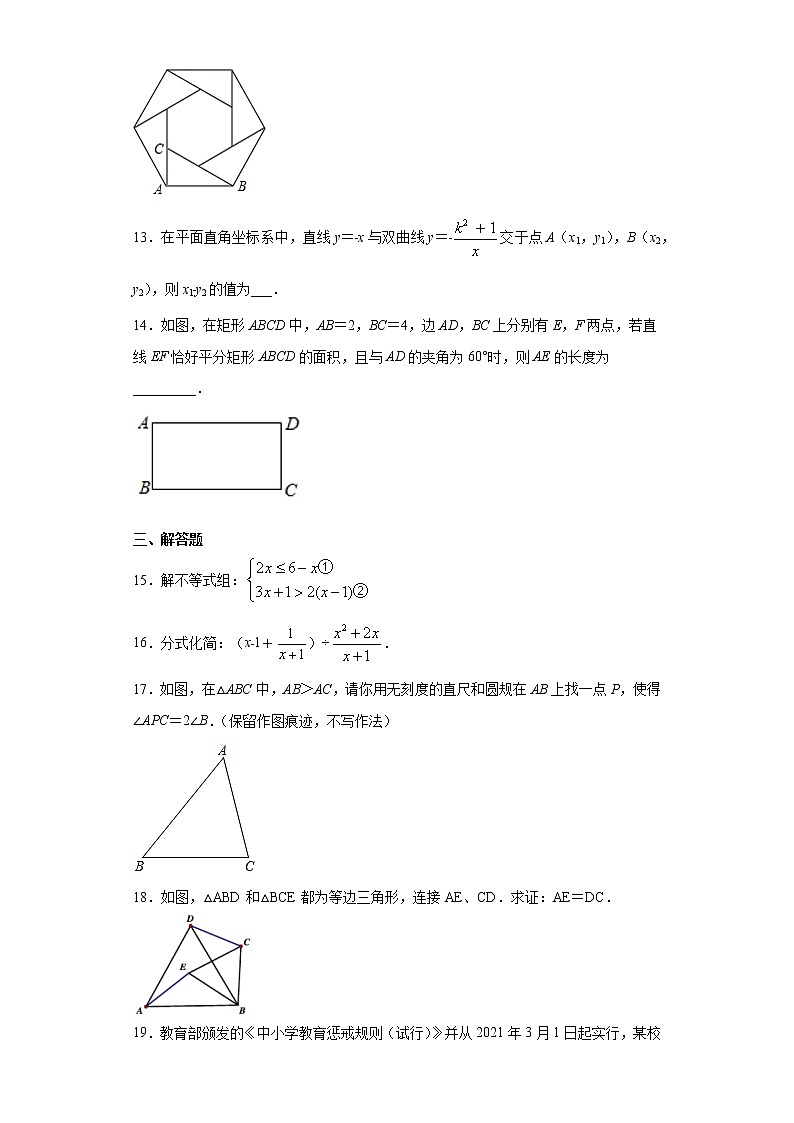
14.如图,在矩形ABCD中,AB=2,BC=4,边AD,BC上分别有E,F两点,若直线EF恰好平分矩形ABCD的面积,且与AD的夹角为60°时,则AE的长度为_________.
三、解答题
15.解不等式组:
16.分式化简:(x﹣1+)÷.
17.如图,在△ABC中,AB>AC,请你用无刻度的直尺和圆规在AB上找一点P,使得∠APC=2∠B.(保留作图痕迹,不写作法)
18.如图,△ABD和△BCE都为等边三角形,连接AE、CD.求证:AE=DC.
19.教育部颁发的《中小学教育惩戒规则(试行)》并从2021年3月1日起实行,某校随机抽取该校部分家长,按四个类别:表示“非常支持”,表示“支持”,表示“不关心”,表示“不支持”,调查他们对该规则态度的情况,将结果绘制成如下两幅不完整的统计图,
根据图中提供的信息,解决下列问题:
(1)这次共抽取了______名家长进行调查统计,扇形统计图中,类所对应的扇形圆心角的大小是______.
(2)将条形统计图补充完整;
(3)该学校共有2000名学生家长,估计该学校家长表示“支持”的(类,类的和)人数大约有多少人?
20.如图1,是我区某村修建于清光绪年间的一座城门,某节假日随父亲回家的张菲同学想利用所学的数学知识测量此城门的高度.
如图2,她站在城门前方点D处,正好看到了城门顶端A点在地面小水潭(近似看成平面镜)里的倒影点C,此时他测得DC的长度为1米;接着她抬起头,目测城门顶端A点的仰角∠α的度数为39°,已知张菲同学的眼睛到地面的距离为1.5米,请你计算城门高度AB(结果精确到1米,sin39°≈0.63,cos39°≈0.78,tan39°≈0.81).
21.某超市,二月底以60元/瓶的成本购进某种洗发露600瓶,并按照80元/瓶的单价销售,销售200瓶后正好遇上“三八妇女节”,商场决定当日以成本价销售,第二日恢复原价后,因库存量较少,超市又以60元/瓶的成本再次购进这种洗发露200瓶,当800瓶洗发露全部销售完后共获利12000元.请你根据下面销售利润y(元)与销售量x(瓶)之间的函数关系图象解答下列问题:
(1)图中m= ,n= ;
(2)求BC的解析式;
(3)利用(2)中结论,计算当销售700瓶时超市获得的利润.
22.在初中毕业理化生实验复习备考中,化学田老师为本班学生准备了下面5个实验项目:A粗盐中难溶性杂质的去除;B.二氧化碳的实验室制取、验满及检验;C镁、锌、铁、铜主要化学性质的探究;D.配置50g质量分数为6%的氯化钠溶液;E.探究物质燃烧的条件.并准备了如图的五等分转盘,规定每名学生可转动一次转盘,并完成转盘停止后指针所指向的实验项目(若指针停在等分线上,则重新转动转盘).
根据数学知识回答下列问题:
(1)小明同学转动一次转盘,正好选中自己熟悉的“A”实验的概率是多少?
(2)请你求出小明和小红两名同学各转动一次转盘,都没有选中“E”实验的概率(用树状图或列表法求解).
23.如图,AB为⊙O的直径,C为BA延长线上一点,CD与⊙O相切于点D.OF⊥AD于点E,交CD于点F.
(1)求证:∠ADC=∠AOF;
(2)若sinC=,BD=10,求EF的长.
24.如图,在平面直角坐标系中,点A的坐标为(﹣1,0),点B,点C分别为x轴,y轴正半轴上一点,其满足OC=OB=2OA.
(1)求过A,B,C三点的抛物线的表达式;
(2)连接CA,CB,若点P是x轴下方抛物线上的一点,连接PC,PB,当S△PCB=S△ACB时,求点P的坐标.
25.(1)如图1,点A和点B是直线上两点,点C和点D是直线上两点,且,BC⊥AB,若AB=2,BC=3,则△ABD的面积为 ;
(2)如图2,在边长为4的菱形ABCD中,∠A=60°,M是边AD的中点,N是边AB上一动点,将△AMN沿直线MN翻折得到△PMN,求点P到直线BC的最小距离;
(3)如图3,在矩形ABCD中,AD=6,AB=8,E,F分别为边CB,CD上的动点,且EF=4,点O为EF的中点,连接BO并延长交CD于点M,过点O作ON∥DC交DB于点N,连接MN,则△BMN面积是否存在最小值?若存在,请求出最小值;若不存在,请说明理由.
参考答案
1.C
【分析】
根据题意列出算式﹣5﹣3,再根据有理数减法的运算法则进行计算即可.
【详解】
解:根据题意得﹣5﹣3=﹣8,
故选:C.
【点睛】
此题主要考查有理数运算的应用,解题的关键是根据题意列式求解.
2.C
【分析】
科学记数法的表示形式为a×10n的形式,其中, n为整数,确定n的值时,要看把原数变成a时,小数点移动了多少位,n的绝对值与小数点移动的位数相同,当原数绝对值>10时,n是正数,当原数的绝对值<1时,n是负数.
【详解】
数字30万用科学记数法表示为,
故选:C.
【点睛】
本题考查科学记数法的表示方法,科学记数法的表示形式为a×10n的形式,其中, n为整数,表示时关键要正确确定 a的值以及n的值.
3.D
【分析】
分别根据合并同类项法则、积的乘方运算法则、平方差公式以及单项式乘单项式的性质,对各个选项逐一判断,即可完成求解.
【详解】
∵a2与a3不是同类项
∴a2与a3不能合并
∴选项A不合题意;
∵
∴选项B不合题意;
∵(a-b)(-a-b)=b2-a2
∴选项C不合题意;
∵2x2(-xy)=-x3y
∴选项D符合题意;
故选:D.
【点睛】
本题考查了整式加减、积的乘方、乘法公式、整式乘法的知识;解题的关键是熟练掌握合并同类项、积的乘方、平方差公式、单项式乘单项式的性质,从而完成求解.
4.A
【分析】
根据平行线的性质可得∠BOD=∠B=75°,再根据平角的性质可得∠ODC=45°,根据三角形外角和定理∠BOD=∠C+∠ODC,即可得出答案.
【详解】
解:∵AB∥EF,∠B=75°,如图,
∴∠BOD=∠B=75°,
又∵∠FDC=135°,
∴∠ODC=45°,
∵∠BOD=∠C+∠ODC,
∴∠C=∠BOD﹣∠ODC=75°﹣45°=30°.
故选:A.
【点睛】
此题主要考查三角形的角度求解,解题的关键是熟知平行线的性质及三角形的外角定理的应用.
5.A
【分析】
将点(a,b)代入y=kx求出k.
【详解】
解:将点(a,b)代入y=kx,解得k=,
∵=2,
∴k==.
故选:A.
【点睛】
此题主要考查正比例函数的解析式,解题的关键是熟知待定系数法的运用.
6.B
【分析】
取AC的中点E,连接EF,DE,由三角形中位线定理得出EF∥BC,EF=DC,证明四边形BDEF是平行四边形,由平行四边形的性质得出BF=DE=2,由直角三角形的性质得出答案.
【详解】
解:取AC的中点E,连接EF,DE,
∵BF是中线,
∴EF∥BC,EF=DC,
∵BD=CD,
∴EF=BD,
∴四边形BDEF是平行四边形,
∴BF=DE=2,
∵AD⊥BC,
∴∠ADC=90°,
∴DE=AC,
∴AC=2DE=4.
故选:B.
【点睛】
此题主要考查三角形内线段长度求解,解题的关键是熟知平行四边形的判定及中位线的性质.
7.B
【分析】
根据对称的性质得出点(﹣1,0)关于y轴对称的对称点,再根据待定系数法确定直线l2的解析式,把x=1代入即可求出交点坐标.
【详解】
解:∵直线l1经过点(﹣1,0),l2经过点(0,2),关于直线x=1对称,
∴点(﹣1,0)关于直线x=1对称点为(3,0),
∴直线l2经过点(3,0),(0,2),
设直线y=kx+2,
代入(3,0)得,3k+2=0,
解得k=﹣,
∴直线l2的解析式为:y=﹣x+2,
把x=1代入得,y=,
∴l1和l2的交点坐标为(1,),
故选:B.
【点睛】
此题主要考查一次函数的图象与性质,解题的关键是熟知待定系数法的应用.
8.C
【分析】
连接AM,延长AM交CD于G,连接FG,由正方形ABCD推出AB=CD=BC=4,AB∥CD,∠C=90°,证得△AEM≌GDM,得到AM=MG,AE=DG=AB,根据三角形中位线定理得到MN=FG,由勾股定理求出FG即可得到MN.
【详解】
解:连接AM,延长AM交CD于G,连接FG,
如图所示:
∵四边形ABCD是正方形,
∴AB=CD=BC=4,AB∥CD,∠C=90°,
∴∠AEM=∠GDM,∠EAM=∠DGM,
∵M为DE的中点,
∴ME=MD,
在△AEM和GDM中,
,
∴△AEM≌△GDM(AAS),
∴AM=MG,AE=DG=AB=CD,
∴CG=CD=2,
∵点N为AF的中点,
∴MN=FG,
∵F为BC的中点,
∴CF=BC=2,
∴FG=,
∴MN=,
故选:C.
【点睛】
本题主要考查了正方形的性质,全等三角形的性质和判定,勾股定理,三角形的中位线定理,正确作出辅助线且证出AM=MG是解题的关键.
9.D
【分析】
由垂径定理得OC⊥AB,则∠BOC=∠AOC=90°,再求出∠ABD=90°﹣∠OEB=25°,然后由圆周角定理得∠AOD=2∠ABD=50°,即可求解.
【详解】
解:∵,
∴OC⊥AB,
∴∠BOC=∠AOC=90°,
∵∠OEB=∠DEC=65°,
∴∠ABD=90°﹣∠OEB=25°,
∴∠AOD=2∠ABD=50°,
∴∠DOC=90°﹣∠AOD=40°,
故选:D.
【点睛】
此题主要考查圆内角度求解,解题的关键是熟知圆周角定理.
10.B
【分析】
先利用二次函数的性质得到抛物线y=ax2+2ax的对称轴为直线x=﹣1,抛物线的开口向上,抛物线与x轴的交点坐标为,利用抛物线的对称性得到关于x的方程ax2+2ax=m(m>0)的另一个根为2,求关于x的方程ax2+2ax=n(0<n<m)的两个整数根就是求直线y=n与抛物线的交点的横坐标,利用图象法得到关于x的方程ax2+2ax=n(0<n<m)有两个整数根能为.
【详解】
抛物线y=ax2+2ax的对称轴为直线x=﹣=﹣1,
∵抛物线y=ax2+2ax在其对称轴的左侧y随x的增大而减小,
∴a>0,抛物线的开口向上,
当y=0时,ax2+2ax=0,解得,
即抛物线y=ax2+2ax与x轴的交点坐标为,如图所示:
∵关于x的方程ax2+2ax=m(m>0)的一个根为﹣4,
∴关于x的方程ax2+2ax=m(m>0)的另一个根为2,
∵关于x的方程ax2+2ax=n(0<n<m)有两个整数根,
∴关于x的方程ax2+2ax=n(0<n<m)有两个整数根能为,
∴这两个根的积是为﹣3.
故选:B.
【点睛】
本题考查了抛物线与x轴的交点:把求二次函数y=ax2+2ax(a,b,c常数,)与x轴的交点坐标问题转化为解关于x的一元二次方程,也考查了二次函数的性质.
11.0(答案不唯一)
【分析】
根据a的范围确定出﹣a的范围,进而确定出b的范围,判断即可.
【详解】
解:由数轴可知,1<a<2,﹣2<﹣a<﹣1,
∵﹣a<b<a,
∴b可以在﹣1和1之间任意取值,如﹣1,0,1等,
故答案为:0(答案不唯一).
【点睛】
此题主要考查数轴的性质,解题的关键是熟知有理数的大小关系.
12.30
【分析】
先证出内部的图形是正六边形,求出内部小正六边形的内角,即可得到∠ACB的度数,根据直角三角形的两个锐角互余即可求解.
【详解】
解:由题意六边形花环是用六个全等的直角三角形拼成,
可得BD=AC,BC=AF,
∴CD=CF,
同理可证小六边形其他的边也相等,即里面的小六边形也是正六边形,
∴∠1=,
∴∠2=180°-120°=60°,
∴∠ABC=30°,
故答案为:30.
【点睛】
本题考查正多边形的证明、多边形的内角和以及三角形的内角和,熟练掌握多边形内角和的计算是解题的关键.
13.0
【分析】
根据正比例函数和反比例函数的对称性得到x1+x2=0,由y2=﹣x2,得出x2=﹣y2,即可得到x1﹣y2=0.
【详解】
解:∵直线y=﹣x与双曲线y=﹣交于点A(x1,y1),B(x2,y2),
∴点A,点B关于原点对称,
∴x1+x2=0,
∵y2=﹣x2,
∴x2=﹣y2,
∴x1﹣y2=0,
故答案为:0.
【点睛】
本题考查了反比例函数与一次函数的交点问题,掌握正比例函数和反比例函数的对称性是本题的关键.
14.2+ .
【分析】
过E、F分别作EG⊥BC、FH⊥AD,交BC、AD于G、H,由所得四边形ABFE和四边形DEFC都是矩形,且等于矩形面积的一半,再根据EF与AD所成角为60°,求出HE,然后再求AE即可.
【详解】
解:如图所示:过E、F分别作EG⊥BC、FH⊥AD,交BC、AD于G、H,
∵EF恰好平分矩形ABCD的面积,
∴梯形AEFB的面积与梯形CFED的面积相等且等于矩形ABCD面积的一半,
即S四边形AEFB=S四边形CFED=×2×4=4,且AE=FC,BF=ED,
又∵在Rt△EFH中,HF=AB=2,
∴HE=HF•tan30°=2×=,
又∵S梯形ABFE=×(AE+BF)×HF=×2×(AE+BF)=AE+BF=4,
AE=AH+HE=BF+HE,
AE+ED=AH+HE+ED=2AH+HE=4,
∴2AH+=4,
AH=2﹣,
∴AE=AH+HE=2﹣+=2+.
故答案为:2+.
【点睛】
此题主要考查矩形的性质应用,解题的关键是熟知梯形的面积公式、三角函数的应用.
15..
【分析】
分别求出各不等式的解集,再找到其公共解集即可求解.
【详解】
解:由①得,
,
.
由②得,
,
.
∴原不等式组的解集是.
【点睛】
本小题考查一元一次不等式组的解法等基础知识,解题的关键是熟知不等式的性质.
16.
【分析】
根据分式的运算法则即可求出答案.
【详解】
解:原式=•
=•
=.
【点睛】
此题主要考查分式的运算,解题的关键是熟知其运算法则.
17.见解析
【分析】
作线段BC的垂直平分线EF,交AB于点P,连接PC,点P即为所求作.
【详解】
解:如图,点P即为所求作.
【点睛】
本题考查作图-复杂作图,线段的垂直平分线的性质,三角形的外角的性质等知识,解题的关键是理解题意,灵活运用所学知识解决问题.
18.见解析
【分析】
先由△ABD和△BCE是等边三角形,可知AB=BD,BE=BC,∠ABD=∠CBE,从而得到∠ABE=∠CBD,即可证明△ABE≌△DBC,从而得到结论.
【详解】
解:证明:∵△ABD和△BCE都为等边三角形,
∴AB=BD,BE=BC,∠ABD=∠CBE,
∴∠ABE=∠CBD,
∴△ABE≌△DBC(SAS),
∴AE=DC.
【点睛】
本题考查的是等边三角形的性质及全等三角形的判定与性质,根据题意判断出△ABE≌△DBC是解答此题的关键.
19.(1)60,;(2)图见解析;(3)1600人.
【分析】
(1)根据条形统计图可以知道类人数,再结合扇形统计图可以知道类所占的百分比求出这次调查统计的人数,再根据条形统计图可以知道类人数,这样就可以求出类所对应的扇形圆心角的大小;
(2)根据(1),可以求出类人数,完成条形统计图即可;
(3)先求出类,类的人数占调查人数的百分比,最后估计学校表示“支持”的(类,类的和)家长的人数.
【详解】
(1)由条形统计图可知类为9人,由扇形统计图可知类所占的百分比为15%,设这次共抽取了名家长进行调查统计,则有,由条形统计图可知类为3人,
所以类所对应的扇形圆心角;
(2)由(1)可知:这次共抽取了60名家长进行调查统计,
因此类为:,条形统计图如下图所示:
;
(3)由(2)可知:类,类的和为,所占调查统计的人数的百分比为:,
因此2000名学生家长,该学校家长表示“支持”的人数约为:,
即在2000名学生家长中,该学校家长表示“支持”的人数约为1600人.
【点睛】
本题考查了通过条形统计和扇形统计图进行有关计算,考查了数学运算能力和数据分析能力,考查了识图能力.
20.2米
【分析】
作EF⊥AB于F,则EF=DB,BF=DE=1.5,证△CDE∽△CAB,得出,代入数值并化简得2AB=3BC,设AB=3x,则BC=2x,EF=DB=CD+BC=1+2x,AF=AB﹣BF=3x﹣1.5,由三角函数的定义得到=0.81,解得x≈2,即可得到AB.
【详解】
解:作EF⊥AB于F,如图,
则EF=DB,BF=DE=1.5,
由题意得:∠DCE=∠ACB,∠EDC=∠ABC=90°,
∴△CDE∽△CAB,
∴,
即,
∴2AB=3BC,
设AB=3x,BC=2x,
则EF=DB=CD+BC=1+2x,AF=AB﹣BF=3x﹣1.5,
在Rt△AEF中,tan∠AEF=tan39°≈0.81=,
即=0.81,
解得:x≈2,
∴AB≈2.
答:算城门高度AB约2米.
【点睛】
本题考查了解直角三角形的应用-仰角俯角问题,相似三角形的判定与性质,解题的关键是正确的构造直角三角形并选择正确的边角关系解直角三角形.
21.(1)4000;400;(2)y=20x﹣4000;(3)销售700瓶时超市获得利润为10000元
【分析】
(1)由题意知m是销售200瓶洗发露时获得的利润,直接由售价减去成本算出,n由总的利润等于售价减去成本算出即可;
(2)利用待定系数法求线段BC的函数的解析式,设y=kx+b,把B(400,4000)和C(800,12000)代入上式得到关于k、b的方程组,解方程组即可;
(3)把x=700代入(2)中解析式即可.
【详解】
解:(1)由题意知:
m=(80﹣60)×200=4000;
(80﹣60)×(200+800﹣n)=12000,
解得:n=400,
故答案为:4000;400.
(2)由(1)知B(400,4000),C(800,12000),
设BC解析式为y=kx+b,把B、C坐标代入得:
,
解得:,
∴BC解析式为y=20x﹣4000.
(3)当x=700时,y=20×700﹣4000=10000,
所以销售700瓶时超市获得利润为10000元.
【点睛】
此题主要考查一次函数的实际应用,解题的关键是熟知待定系数法的应用.
22.(1);(2)
【分析】
(1)直接由概率公式求解即可;
(2)画树状图,共有25个等可能的结果,再找出符合条件的结果数,然后由概率公式求解即可.
【详解】
解:(1)小明同学转动一次转盘,正好选中自己熟悉的“A”实验的概率是;
(2)画树状图如图:
共有25个等可能的结果,小明和小红两名同学都没有选中“E”实验的结果有16个,
∴小明和小红两名同学各转动一次转盘,都没有选中“E”实验的概率为.
【点睛】
此题主要考查概率的求解,解题的关键是根据题意列出树状图及概率公式的运用.
23.(1)见解析;(2)
【分析】
(1)连接OD,由切线的性质得到∠ADC+∠ADO=90°,由等腰三角形的性质得到∠DAO=∠ADO,根据∠AOF+∠DAO=90°,由等量代换即可得到结论;
(2)根据三角形中位线定理得到OE=BD=5,设OD=3x,OC=5x,根据相似三角形的性质即可得到结论.
【详解】
(1)证明:连接OD,
∵OF⊥AD,
∴∠AOF+∠DAO=90°,
∵CD是⊙O的切线,D为切点,
∴∠CDO=90°,
∴∠ADC+∠ADO=90°,
∵OA=OD,
∴∠DAO=∠ADO,
∴∠AOF=∠ADC;
(2)解:∵AB是直径,
∴∠ADB=90°,
又OF⊥AD,
∴OFBD,
∵AO=OB,
∴AE=DE,
∴OE=BD=10=5,
∵sinC=,
∴设OD=3x,OC=5x,
∴OB=3x,
∴CB=8x,
∵OF∥BD,
∴△COF∽△CBD,
∴,
∴,
∴OF=,
∴EF=OF﹣OE=﹣5=.
【点睛】
此题主要考查圆的切线的判定与性质,解题的关键是熟知切线的判定定理、三角函数的应用及相似三角形的判定与性质.
24.(1)y=﹣x2+x+2;(2)点P的坐标为(1+,﹣3﹣)或(1﹣,﹣3)
【分析】
(1)由线段长度求出三个点的坐标,再用待定系数法求解即可;
(2)利用待定系数法求出直线PC的解析式,设P(m,﹣m2+m+2),然后表示出S△PCB,然后利用S△PCB求出m的值,即可求出P点的坐标.
【详解】
解:(1)∵点A的坐标为(﹣1,0),OC=OB=2OA.
∴B(2,0),C(0,2),
设过A、B、C三点的抛物线的解析式为y=a(x﹣2)(x+1),
把点C(0,2)代入,解得:a=﹣1,
所以抛物线的解析式为:y=﹣(x﹣2)(x+1)=﹣x2+x+2;
(2)如图,
∵S△ACB=AB•OC=×3×2=3,
∴S△PCB=S△ACB=4,
∵点P是x轴下方抛物线上的一点,设P(m,﹣m2+m+2),
∴直线PC为y=(﹣m+1)x+2,y=0时,x=,m<﹣1或m>2,
∴S△PCB=BM•[2﹣(﹣m2+m+2)]=×(2﹣)×(m2﹣m)=4,
解得:m1=1+,m2=1﹣,
∴点P的坐标为(1+,﹣3﹣)或(1﹣,﹣3).
【点睛】
此题主要考查二次函数与几何综合,解题的关键是熟知三角形的面积公式与解析式的求解方法.
25.(1)3;(2)2﹣2;(3)存在,14
【分析】
(1)求出三角形ABC的面积为3,由平行线的性质可得出答案;
(2)过点M作ME⊥BC于点E,交圆M于点P,则PE的值是最小值,由直角三角形的性质及菱形的性质可得出答案;
(3)过点O作OJ⊥BD于J,过点C作CK⊥BD于K.由平行线的性质得出S△BMN=•ON•AD=3ON,由直角三角形的性质求出OJ的最小值,则可求出ON的最小值,则可得出答案.
【详解】
解:(1)∵BC⊥AB,AB=2,BC=3,
∴S△ABC=×AB×BC=×2×3=3,
∵l1∥l2,
∴S△ABD=S△ABC=3.
故答案为:3.
(2)如图2,由折叠知MP=AM,又M是AD的中点,可得MA=MP=MD,
故点P在以AD为直径的圆上,
过点M作ME⊥BC于点E,交圆M于点P,则PE的值是最小值,
∵∠A=60°,AB=4,
∴AM=2,
∴ME=2,
∴PE=2﹣2.
∴点P到直线BC的最小距离是2﹣2;
(3)存在.
理由:如图3中,过点O作OJ⊥BD于J,过点C作CK⊥BD于K.
∵ON∥CD,AB∥CD,
∴ON∥AB,
∴S△BMN=•ON•AD=3ON,
∴ON的值最小时,△BMN的面积最小,
∵四边形ABCD是矩形,
∴∠A=90°,AD=6,AB=8,
∴BD==10,
∵CK⊥BD,
∴S△BCD=•CD•CB=•BD•CK,
∴CK=,
∵ON∥AB,
∴∠ONJ=∠ABD,
∴cos∠ONJ=cos∠ABD=,
∵∠OJN=90°,
∴OJ=ON,
∵OJ⊥BD,CK⊥BD,
∴CO+OJ≥CK,
∵∠ECF=90°,EF=4,FO=EF,
∴CO=EF=2,
∴2+OJ≥,
∴OJ≥,
∴OJ的最小值为,
∴ON的最小值为,
∴△BMN的面积的最小值为3×=14.
【点睛】
此题主要考查四边形综合,解题的关键是熟知三角形的面积公式、圆的基本性质及三角函数的应用.
2023年陕西省西安市长安区中考数学二模试卷(含解析): 这是一份2023年陕西省西安市长安区中考数学二模试卷(含解析),共21页。试卷主要包含了选择题,填空题,解答题等内容,欢迎下载使用。
2023年陕西省西安市长安区中考数学二模试卷(含解析): 这是一份2023年陕西省西安市长安区中考数学二模试卷(含解析),共21页。试卷主要包含了选择题,填空题,解答题等内容,欢迎下载使用。
2022年陕西省西安市长安区中考数学二模试卷(word版含答案): 这是一份2022年陕西省西安市长安区中考数学二模试卷(word版含答案),共25页。













