

2021年陕西省西安市未央区中考数学三模试卷 word版,解析版
展开2021年陕西省西安市未央区中考数学三模试卷
一、选择题(共10小题,每小题3分,计30分.每小题只有一个选项是符合题意的)
1.(3分)|﹣2021|的相反数是( )
A.2021 B. C.﹣2021 D.
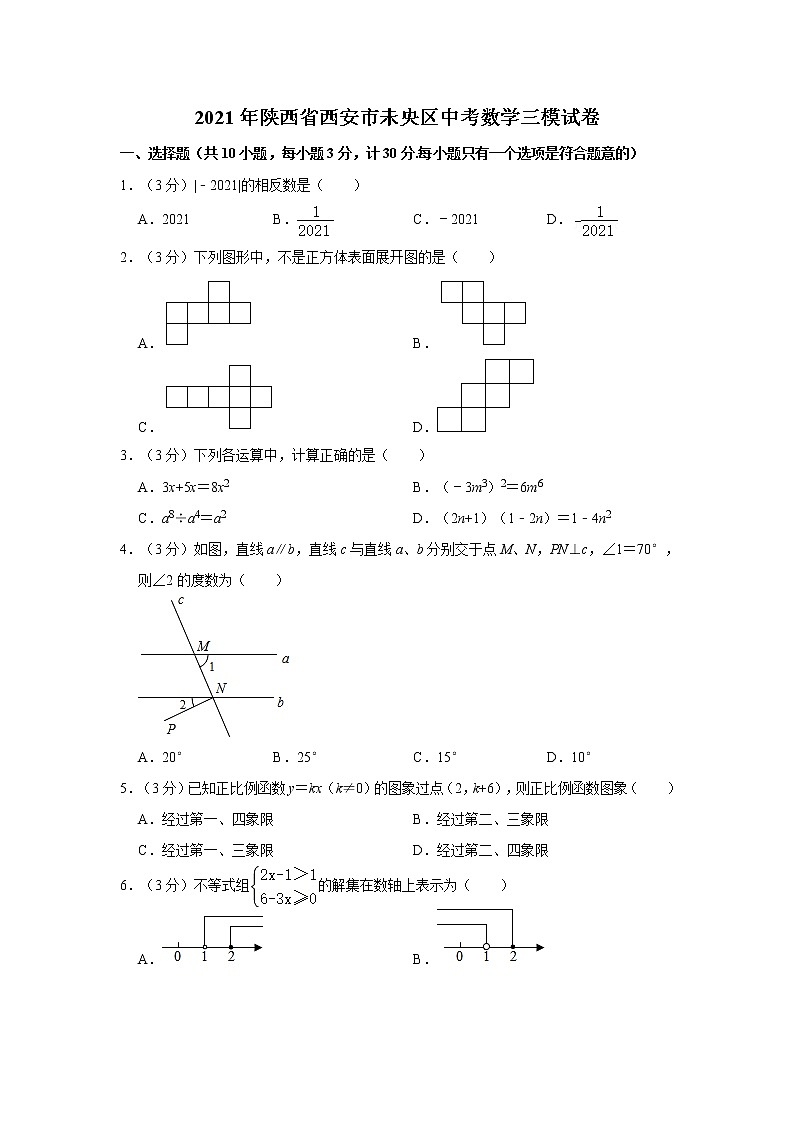
2.(3分)下列图形中,不是正方体表面展开图的是( )
A. B.
C. D.
3.(3分)下列各运算中,计算正确的是( )
A.3x+5x=8x2 B.(﹣3m3)2=6m6
C.a8÷a4=a2 D.(2n+1)(1﹣2n)=1﹣4n2
4.(3分)如图,直线a∥b,直线c与直线a、b分别交于点M、N,PN⊥c,∠1=70°,则∠2的度数为( )
A.20° B.25° C.15° D.10°
5.(3分)已知正比例函数y=kx(k≠0)的图象过点(2,k+6),则正比例函数图象( )
A.经过第一、四象限 B.经过第二、三象限
C.经过第一、三象限 D.经过第二、四象限
6.(3分)不等式组的解集在数轴上表示为( )
A. B.
C. D.
7.(3分)如图,菱形ABCD的对角线AC、BD相交于点O,AC=10,BD=4,EF为过点O的一条直线,则图中阴影部分的面积为( )
A.5 B.6 C.8 D.12
8.(3分)如图,AB是⊙O的直径,弦AC=OB,D是半圆AB的中点,连接CD交AB于点E,则∠BEC的大小为( )
A.60° B.65° C.70° D.75°
9.(3分)如图,在Rt△ABC中,∠ABC=90°,AB=8,BC=6,D是AC的中点,AF平分∠BAC交BD于点E,则BE的长为( )
A. B.3 C. D.
10.(3分)已知二次函数y=ax2+bx+c的图象与x轴交于点(﹣2,0)、(x1,0).且1<x1<2,与y轴的负半轴相交.则下列关于a、b的大小关系正确的是( )
A.a>0>b B.a>b>0 C.b>a>0 D.b<a<0
二、填空题(共4小题,每小题3分,计12分)
11.(3分)在实数,﹣,3.14159,,中,无理数是 .
12.(3分)正九边形的每一个内角是 度.
13.(3分)如图,在平面直角坐标系中,B(﹣2,0),AB⊥OB,反比例函数y=(x<0)的图象与AB交于点C,与OA交于点E,且AC=3BC,S△AOC=3,则点E的坐标为 .
14.(3分)如图,四边形ABCD中,∠B=60°,AB=BC,将边DA绕点D逆时针旋转60°得到线段DE,过点E做EF⊥BC,垂足为F,若EF=2,BF=3,则线段CD的长是 .
三、解答题(共11小题,计78分.解答应写出过程)
15.(5分)计算:.
16.(5分)计算:(1﹣).
17.(5分)如图,在Rt△ABC中,∠ABC=90°,D是斜边AC上一点,在射线BD上用尺规作一点E,使∠BEC=∠A(不写作法,保留作图痕迹).
18.(5分)如图,在四边形ABCD中,AD=BC,连接BD,E是BC延长线上一点,连接DE,且BD=DE,∠E=∠ADB,求证:∠A=∠BCD.
19.(7分)健康的体魄是青少年为祖国和人民服务的其本前提,是中华民族旺盛生命力的体现.某初中学校为了增强学生体质健康,制定合理的校园阳光体育锻炼方案,随机抽查了部分学生最近两周参加晨跑锻炼活动的天数,并用得到的数据绘制了两幅不完整的统计图:
请根据图中提供的信息,回答下列问题:
(1)补全条形统计图;
(2)本次抽样调查的参加晨跑锻炼活动的天数的众数为 ,中位数为 ;
(3)如果该校约有3500名学生,请你估计全校有多少名学生参加体育晨跑的天数不少于7?
20.(7分)在陕西省洛南县有一右手执刀笔,左手持结绳的古人雕像,是为了纪念中华汉字造字始祖仓颉而建.因不能直接测量,小凯和同学小段想利用所学知识来测量雕像的高度.如图,小凯站在雕像(AB)旁的水平地面上D处,小段在BD之间的水平地面上放置一个平面镜并来回移动,当平面镜移动到点E时,小凯刚好在平面境内看到雕像顶端A,此时测得DE=0.9米,小凯眼睛距地面的高度CD=1.8米,然后小段在距离小凯4.1米的点G处用测角仪测得雕像顶端A处的仰角为40°,测角仪FG=1.6米.已知G、D、E、B在同一水平线上,AB、CD、FG都垂直GB,请根据以上信息,求出雕像的高(AB的长).(参考数据:sin40°=0.64,cos40°=0.77,tan40°=0.84)
21.(7分)学校为继续做好疫情防控工作,守护师生健康,欲购买单价为20元的消毒液和单价为80元的免洗洗手液共100瓶.设购买消毒液x瓶,购买两种防疫用品的总费用为y元.
(1)请求出y与x的函数关系式,并写出自变量x的取值范围;
(2)若免洗洗手液瓶数不少于消毒液瓶数的3倍,则购买这两种防疫用品各多少瓶时,花费最少,此时的花费是多少元?
22.(7分)为培养学生的动手操作能力,提高学生的化学实验素养,备考2021年初中学业水平考试化学实验操作,某校进行了化学实验模考,要求学生从下列6个实验中抽取并完成.
A.粗盐中难溶性杂质的去除
B.二氧化碳的实验室制取、验满及检验
C.镁、锌、铁、铜主要化学性质的探究
D.配制50g质量分数为6%的氯化钠溶液
E.探究物质燃烧的条件
F.碱的主要化学性质
(1)若某同学从中抽取一个实验,求某同学抽到实验C的概率;
(2)若某同学从中抽取两个实验,请用列表或画树状图的方法,求抽到实验A和实验F的概率.
23.(8分)如图,在Rt△ABC中,BC=6,BD是斜边AC上的高,延长BD交Rt△ABC外接圆⊙O于点E,过E作⊙O的切线EF交BC的延长线于点F,连接AF交BE于点G,EF∥AB.
(1)求证:∠AEB=60°;
(2)求FG的长.
24.(10分)已知抛物线L1:y=ax2+bx(a≠0)经过A(﹣2,4)、B(﹣4,4)两点.
(1)求抛物线L1的函数表达式;
(2)先将抛物线L1沿x轴翻折,再向右平移m(m>0)个单位长度,得到抛物线L2,L2与y轴交于点C,点D为抛物线L2上一点.要使以AB为边,A、B、C、D为顶点的四边形为平行四边形,求所有满足条件的抛物线L2的函数表达式.
25.(12分)(1)问题提出:如图①,在矩形ABCD中,AB=1,BC=,P是AD上一动点,则BP+PD的最小值为 .
(2)问题探究:如图②,在正方形ABCD中,AB=3,点是平面上一点,且CE=1,连接BE,在BE上方作正方形BEMN,求BM的最大值.
(3)问题解决:为迎接2021年9月在西安举办的第14届全运会,打造体育历史文化名城,某小区对一正方形区域ABCD进行设计改造,方便大家锻炼运动.如图③,在正方形内设计等腰直角△CEF为健身运动区域,直角顶点E设计在草坪区域扇形MBN的弧MN上.设计铺设CF和DF这两条不同造价鹅卵石路,已知AB=40米,BM=10米,∠CEF=90°,CE=EF,若铺设CF路段造价为每米200元,铺设DF路段的造价为每米100元,请求出铺设CF和DF两条路段的总费用的最小值.
2021年陕西省西安市未央区中考数学三模试卷
参考答案与试题解析
一、选择题(共10小题,每小题3分,计30分.每小题只有一个选项是符合题意的)
1.(3分)|﹣2021|的相反数是( )
A.2021 B. C.﹣2021 D.
【分析】根据相反数的概念解答即可.
【解答】解:|﹣2021|=2021,
2021的相反数是﹣2021,
故选:C.
2.(3分)下列图形中,不是正方体表面展开图的是( )
A. B.
C. D.
【分析】根据正方体展开图的11种形式对各小题分析判断即可得解.
【解答】解:A、B、D均是正方体表面展开图;
C、正方体有6个面,C有7个小正方形,故不是正方体表面展开图.
故选:C.
3.(3分)下列各运算中,计算正确的是( )
A.3x+5x=8x2 B.(﹣3m3)2=6m6
C.a8÷a4=a2 D.(2n+1)(1﹣2n)=1﹣4n2
【分析】分别根据合并同类项法则,积的乘方运算法则,同底数幂的除法法则以及平方差公式逐一判断即可.
【解答】解:A、3x+5x=8x,故本选项不合题意;
B、(﹣3m3)2=9m6,故本选项不合题意;
C、a8÷a4=a4,故本选项不合题意;
D、(2n+1)(1﹣2n)=1﹣4n2,故本选项符合题意;
故选:D.
4.(3分)如图,直线a∥b,直线c与直线a、b分别交于点M、N,PN⊥c,∠1=70°,则∠2的度数为( )
A.20° B.25° C.15° D.10°
【分析】根据平行线的性质得出∠1=∠3=70°,根据PN⊥c求出∠MNP=90°,即可求解.
【解答】解:∵PN⊥c,
∴∠MNP=90°,
∵a∥b,∠1=70°,
∴∠1=∠3=70°,
∴∠2=∠MNP﹣∠3=20°,
故选:A.
5.(3分)已知正比例函数y=kx(k≠0)的图象过点(2,k+6),则正比例函数图象( )
A.经过第一、四象限 B.经过第二、三象限
C.经过第一、三象限 D.经过第二、四象限
【分析】由点(2,k+6)在正比例函数的图象上,利用一次函数图象上点的坐标特征可求出k值,再利用正比例函数的性质可得出正比例函数图象经过的象限.
【解答】解:∵正比例函数y=kx(k≠0)的图象过点(2,k+6),
∴k+6=2k,
∴k=6.
又∵k=6>0,
∴正比例函数y=6x的图象经过第一、三象限.
故选:C.
6.(3分)不等式组的解集在数轴上表示为( )
A. B.
C. D.
【分析】先求出不等式的解集,再求出不等式组的解集,最后在数轴上表示出不等式组的解集即可.
【解答】解:,
∵解不等式①得:x>1,
解不等式②得:x≤2,
∴不等式组的解集是:1<x≤2,
在数轴上表示为:,
故选:C.
7.(3分)如图,菱形ABCD的对角线AC、BD相交于点O,AC=10,BD=4,EF为过点O的一条直线,则图中阴影部分的面积为( )
A.5 B.6 C.8 D.12
【分析】由“ASA”可证△AEO≌△CFO,可得S△AEO=S△CFO,即可求解.
【解答】解:∵四边形ABCD是菱形,
∴AC⊥BD,AO=CO,AD∥BC,
∴∠DAO=∠BCO,
在△AEO和△CFO中,
,
∴△AEO≌△CFO(ASA),
∴S△AEO=S△CFO,
∴图中阴影部分的面积=S△BOC=S菱形ABCD=×=5,
故选:A.
8.(3分)如图,AB是⊙O的直径,弦AC=OB,D是半圆AB的中点,连接CD交AB于点E,则∠BEC的大小为( )
A.60° B.65° C.70° D.75°
【分析】连接AD,BD,过点O作OH⊥AC于H.证明△ABD是等腰直角三角形,解直角三角形求出∠EAC可得结论.
【解答】解:连接AD,BD,过点O作OH⊥AC于H.
∵=,
∴AD=BD,
∵AB是直径,
∴∠ADB=90°,
∴∠ABD=45°,
∴∠ACD=∠ABD=45°,
∵OH⊥AC,
∴AH=HC,
∵AC=OB,AO=OB,
∴cos∠OAH==,
∴∠OAH=30°,
∴∠CEB=∠ACE+∠EAC=75°,
故选:D.
9.(3分)如图,在Rt△ABC中,∠ABC=90°,AB=8,BC=6,D是AC的中点,AF平分∠BAC交BD于点E,则BE的长为( )
A. B.3 C. D.
【分析】过点F作FG⊥AC于G,作DH∥AF交BC于H,根据角平分线的性质求出BF=FG,证明△CGF∽△CBA,由相似三角形的性质可得BF=,则CF=,根据三角形中位线定理可得FH=CF=,再证△BEF∽△BDH,由相似三角形的性质即可求解.
【解答】解:过点F作FG⊥AC于G,作DH∥AF交BC于H,
在Rt△ABC中,∠ABC=90°,AB=8,BC=6,D是AC的中点,
∴BD=AC,AC==10,
∴BD=5,
∵AF平分∠BAC,FG⊥AC,∠ABC=90°,
∴BF=FG,
∵∠C=∠C,∠CGF=∠CBA=90°,
∴△CGF∽△CBA,
∴,即,
∴BF=,
∴CF=BC﹣BF=,
∵D是AC的中点,DH∥AF,
∴DH是△AFC的中位线,
∴FH=CF=,
∴BH=BF+FH=,
∵DH∥AF,
∴△BEF∽△BDH,
∴,即,
∴BE=.
故选:C.
10.(3分)已知二次函数y=ax2+bx+c的图象与x轴交于点(﹣2,0)、(x1,0).且1<x1<2,与y轴的负半轴相交.则下列关于a、b的大小关系正确的是( )
A.a>0>b B.a>b>0 C.b>a>0 D.b<a<0
【分析】首先根据题意画出草图,再根据抛物线的开口方向和对称轴的位置确定a、b的大小和符号即可.
【解答】解:根据题意画出草图,
可得抛物线开口向上,则a>0,
∵1<x1<2,
∴﹣1<﹣2+x1<0
∴﹣<<0,
∴对称轴在y轴左侧,
∴a、b同号,
∴b>0,
∵﹣,
∴<1,
∴b<a,
∴a>b>0,
故选:B.
二、填空题(共4小题,每小题3分,计12分)
11.(3分)在实数,﹣,3.14159,,中,无理数是 .
【分析】无理数就是无限不循环小数.理解无理数的概念,一定要同时理解有理数的概念,有理数是整数与分数的统称.即有限小数和无限循环小数是有理数,而无限不循环小数是无理数.
【解答】解:是分数,属于有理数;
﹣=2,是整数,属于有理数;
3.14159是有限小数,属于有理数;
=﹣3,是整数,属于有理数;
是无理数.
故答案为:.
12.(3分)正九边形的每一个内角是 140 度.
【分析】先求出该多边形的内角和,再求出每一个内角的度数.
【解答】解:180°•(9﹣2)÷9=140°.
13.(3分)如图,在平面直角坐标系中,B(﹣2,0),AB⊥OB,反比例函数y=(x<0)的图象与AB交于点C,与OA交于点E,且AC=3BC,S△AOC=3,则点E的坐标为 (﹣1,2) .
【分析】根据B(﹣2,0),AB⊥OB得出点C坐标,再通过S△AOC=3求出AC长度,由AC=3BC可得点A坐标,解出AO所在直线解析式然后联立方程求解.
【解答】解:∵B(﹣2,0),AB⊥OB,
∴点A横坐标为﹣2,OB=2,
∵S△AOC=OB•AC=3,
∴AC===3,
∵AC=3BC,
∴BC=AC=1,
∴点C坐标为(﹣2,1),AB=AC+BC=4,点A坐标为(﹣2,4),
∴k=﹣2×1=﹣2.
∴y=﹣,
设直线OA解析式为y=mx,
将A(﹣2,4)代入y=mx可得m=﹣2,
即y=﹣2x.
联立方程,
解得x=﹣1或x=1(舍),
将x=﹣1代入y=﹣2x得y=2,
∴点E坐标为(﹣1,2).
故答案为:(﹣1,2).
14.(3分)如图,四边形ABCD中,∠B=60°,AB=BC,将边DA绕点D逆时针旋转60°得到线段DE,过点E做EF⊥BC,垂足为F,若EF=2,BF=3,则线段CD的长是 .
【分析】由勾股定理可求BE的长,由“SAS”可证△ABE≌△ACD,可得BE=CD=.
【解答】解:如图,连接AC,AE,BE,
∵EF=2,BF=3,
∴BE===,
∵∠B=60°,AB=BC,
∴△ABC是等边三角形,
∴AB=AC,∠BAC=60°,
∵将边DA绕点D逆时针旋转60°得到线段DE,
∴AD=AE,∠ADE=60°,
∴△ADE是等边三角形,
∴AE=AD,∠DAE=60°,
∴∠DAE=∠BAC,
∴∠BAE=∠DAC,
在△ABE和△ACD中,
,
∴△ABE≌△ACD(SAS),
∴BE=CD=,
故答案为:.
三、解答题(共11小题,计78分.解答应写出过程)
15.(5分)计算:.
【分析】根据二次根式的性质以及负整数指数幂的意义即可求出答案.
【解答】解:原式=3﹣﹣(3﹣)+
=3﹣﹣3++
=.
16.(5分)计算:(1﹣).
【分析】原式括号中两项通分并利用同分母分式的减法法则计算,同时利用除法法则变形,约分即可得到结果.
【解答】解:原式=•=.
17.(5分)如图,在Rt△ABC中,∠ABC=90°,D是斜边AC上一点,在射线BD上用尺规作一点E,使∠BEC=∠A(不写作法,保留作图痕迹).
【分析】先作AC的垂直平分线得到AC的中点O,再作△ABC为外接圆⊙O,则⊙O与射线AD的交点为E,利用圆周角定理可确定E点满足条件.
【解答】解:如图,点E为所作.
18.(5分)如图,在四边形ABCD中,AD=BC,连接BD,E是BC延长线上一点,连接DE,且BD=DE,∠E=∠ADB,求证:∠A=∠BCD.
【分析】由等腰三角形的性质和已知得∠DBE=∠ADB,则AD∥BC,再证四边形ABCD是平行四边形,即可得出结论.
【解答】证明:∵BD=DE,
∴∠E=∠DBE,
∵∠E=∠ADB,
∴∠DBE=∠ADB,
∴AD∥BC,
又∵AD=BC,
∴四边形ABCD是平行四边形,
∴∠A=∠BCD.
19.(7分)健康的体魄是青少年为祖国和人民服务的其本前提,是中华民族旺盛生命力的体现.某初中学校为了增强学生体质健康,制定合理的校园阳光体育锻炼方案,随机抽查了部分学生最近两周参加晨跑锻炼活动的天数,并用得到的数据绘制了两幅不完整的统计图:
请根据图中提供的信息,回答下列问题:
(1)补全条形统计图;
(2)本次抽样调查的参加晨跑锻炼活动的天数的众数为 5天 ,中位数为 6天 ;
(3)如果该校约有3500名学生,请你估计全校有多少名学生参加体育晨跑的天数不少于7?
【分析】(1)根据锻炼5天的人数和所占的百分比,可以计算出本次调查的人数,然后即可计算出锻炼8天的人数,从而可以将条形统计图补充完整;
(2)根据条形统计图中的数据,可以写出相应的众数和中位数;
(3)根据条形统计图中的数据,可以计算出全校有多少名学生参加体育晨跑的天数不少于7.
【解答】解:(1)本次调查的人数为:240÷40%=600,
锻炼8天的有:600﹣240﹣120﹣150﹣30=60(人),
补全的条形统计图如右图所示;
(2)由条形统计图可得,
众数是5天,中位数是6天,
故答案为:5天,6天;
(3)3500×=1400(名),
即估计全校有1400名学生参加体育晨跑的天数不少于7.
20.(7分)在陕西省洛南县有一右手执刀笔,左手持结绳的古人雕像,是为了纪念中华汉字造字始祖仓颉而建.因不能直接测量,小凯和同学小段想利用所学知识来测量雕像的高度.如图,小凯站在雕像(AB)旁的水平地面上D处,小段在BD之间的水平地面上放置一个平面镜并来回移动,当平面镜移动到点E时,小凯刚好在平面境内看到雕像顶端A,此时测得DE=0.9米,小凯眼睛距地面的高度CD=1.8米,然后小段在距离小凯4.1米的点G处用测角仪测得雕像顶端A处的仰角为40°,测角仪FG=1.6米.已知G、D、E、B在同一水平线上,AB、CD、FG都垂直GB,请根据以上信息,求出雕像的高(AB的长).(参考数据:sin40°=0.64,cos40°=0.77,tan40°=0.84)
【分析】如图,过F作FH⊥AB于H,得到四边形BGFH是矩形,求得BH=GF=1.6米,BG=HF,设AB=x米,根据相似三角形的性质得到BE=0.5x,由三角函数的定义即可得到结论.
【解答】解:如图,过F作FH⊥AB于H,
∵AB⊥BG,CD⊥BG,FG⊥BG,
∴四边形BGFH是矩形,
∴BH=GF=1.6米,BG=HF,
设AB=x米,
由题意得,∠CED=∠AEB,∠CDE=∠ABE,
∴△CDE∽△ABE,
∴,
即,
解得:BE=0.5x,
∴HF=BG=GD+DE+BE=(5+0.5x)(m),
∵∠AFH=40°,AH=(x﹣1.6)m,
∴tan∠AFH==≈0.84,
解得:x≈10,
∴雕像的高为10m.
21.(7分)学校为继续做好疫情防控工作,守护师生健康,欲购买单价为20元的消毒液和单价为80元的免洗洗手液共100瓶.设购买消毒液x瓶,购买两种防疫用品的总费用为y元.
(1)请求出y与x的函数关系式,并写出自变量x的取值范围;
(2)若免洗洗手液瓶数不少于消毒液瓶数的3倍,则购买这两种防疫用品各多少瓶时,花费最少,此时的花费是多少元?
【分析】(1)购买消毒液x瓶,则购买免洗洗手液(100﹣x)瓶,根据题意可列y=20x+80(100﹣x),因为100﹣x≥0,既0≤x≤100,化简即可得出答案;
(2)先根据免洗洗手液瓶数不少于消毒液瓶数的3倍,所以100﹣x≥3x,根据一次函数的性质,k<0,y随x的增大而减小,即x=25时,y有最小值,代入即可得出答案.
【解答】解:(1)y=20x+80(100﹣x)=﹣60x+8000(0≤x≤100).
(2)∵免洗洗手液瓶数不少于消毒液瓶数的3倍,
∴100﹣x≥3x,
∴x≤25.
∵y=﹣60x+8000,
﹣60<0,
∴y随x的增大而减小,
∴x=25时,y最小,此时y=﹣60×25+8000=6500,
∴当购买消毒液25瓶,免洗洗手液75瓶时,花费最少,最少花费6500元.
22.(7分)为培养学生的动手操作能力,提高学生的化学实验素养,备考2021年初中学业水平考试化学实验操作,某校进行了化学实验模考,要求学生从下列6个实验中抽取并完成.
A.粗盐中难溶性杂质的去除
B.二氧化碳的实验室制取、验满及检验
C.镁、锌、铁、铜主要化学性质的探究
D.配制50g质量分数为6%的氯化钠溶液
E.探究物质燃烧的条件
F.碱的主要化学性质
(1)若某同学从中抽取一个实验,求某同学抽到实验C的概率;
(2)若某同学从中抽取两个实验,请用列表或画树状图的方法,求抽到实验A和实验F的概率.
【分析】(1)直接由概率公式求解即可;
(2)画树状图,共有30个等可能的结果,抽到实验A和实验F的结果有2个,再由概率公式求解即可.
【解答】解:(1)若某同学从中抽取一个实验,则某同学抽到实验C的概率为;
(2)画树状图如图:
共有30个等可能的结果,抽到实验A和实验F的结果有2个,
∴抽到实验A和实验F的概率为=.
23.(8分)如图,在Rt△ABC中,BC=6,BD是斜边AC上的高,延长BD交Rt△ABC外接圆⊙O于点E,过E作⊙O的切线EF交BC的延长线于点F,连接AF交BE于点G,EF∥AB.
(1)求证:∠AEB=60°;
(2)求FG的长.
【分析】(1)连接EO并延长交AB于H,根据切线的性质得到OE⊥EF,根据线段垂直平分线的性质得到AE=BE,AB=AE,于是得到△ABE是等边三角形,根据等边三角形的性质得到结论;
(2)根据等边三角形的性质得到∠BAD=30°,AB=BC=6,AC=12,求得OE=AC=6,OH=BC=3,根据矩形的性质得到BF=EH+OH+OE=3+6=9,EF=BH=AB,根据勾股定理得到AF==3,根据平行线分线段成比例定理即可得到结论.
【解答】(1)证明:连接EO并延长交AB于H,
∵EF是⊙O的切线,
∴OE⊥EF,
∵EF∥AB,
∴AH=BH,
∴EH垂直平分AB,
∴AE=BE,
同理,AD垂直平分BE,
∴AB=AE,
∴△ABE是等边三角形,
∴∠AEB=60°;
(2)解:∵△ABE是等边三角形,AD⊥BE,
∴∠BAD=30°,AB=BC=6,AC=12,
∴OE=AC=6,OH=BC=3,
∵OH⊥AB,OE⊥EF,AB⊥BC,
∴四边形EFBH是矩形,
∴BF=EH+OH+OE=3+6=9,EF=BH=AB,
在Rt△ABF中,AF==3,
∵EF∥AB,
∴=,
∴FG=AF=.
24.(10分)已知抛物线L1:y=ax2+bx(a≠0)经过A(﹣2,4)、B(﹣4,4)两点.
(1)求抛物线L1的函数表达式;
(2)先将抛物线L1沿x轴翻折,再向右平移m(m>0)个单位长度,得到抛物线L2,L2与y轴交于点C,点D为抛物线L2上一点.要使以AB为边,A、B、C、D为顶点的四边形为平行四边形,求所有满足条件的抛物线L2的函数表达式.
【分析】(1)将点A(﹣2,4)、B(﹣4,4)分别代入解析式可求抛物线L1的解析式,由轴对称和平移的性质可求解;
(2)由二次函数图象与几何变换规律写出抛物线L2上解析式;然后由平行四边形的性质和点与坐标的性质可求解.
【解答】解:(1)将点A(﹣2,4)、B(﹣4,4)分别代入抛物线L1:y=ax2+bx,得.
解得.
故抛物线L1的函数表达式为:y=﹣x2﹣3x;
(2)如图,将抛物线L1沿x轴翻折后的表达式为:y=(x+3)2﹣,再向右平移m个单位长度后,得抛物线L2:y=(x+3﹣m)2﹣,
∵以AB为边,A、B、C、D为顶点的四边形为平行四边形,A(﹣2,4)、B(﹣4,4),
∴AB∥x轴.
∴点C的坐标是(0,﹣4).
将点C的坐标代入表达式得:﹣4=(0+3﹣m)2﹣,
解得m=2或4.
故抛物线L2的函数表达式为:y=(x+1)2﹣或y=(x﹣1)2﹣.
25.(12分)(1)问题提出:如图①,在矩形ABCD中,AB=1,BC=,P是AD上一动点,则BP+PD的最小值为 .
(2)问题探究:如图②,在正方形ABCD中,AB=3,点是平面上一点,且CE=1,连接BE,在BE上方作正方形BEMN,求BM的最大值.
(3)问题解决:为迎接2021年9月在西安举办的第14届全运会,打造体育历史文化名城,某小区对一正方形区域ABCD进行设计改造,方便大家锻炼运动.如图③,在正方形内设计等腰直角△CEF为健身运动区域,直角顶点E设计在草坪区域扇形MBN的弧MN上.设计铺设CF和DF这两条不同造价鹅卵石路,已知AB=40米,BM=10米,∠CEF=90°,CE=EF,若铺设CF路段造价为每米200元,铺设DF路段的造价为每米100元,请求出铺设CF和DF两条路段的总费用的最小值.
【分析】(1)以PD为斜边构造30°的直角三角形,则PB+PD=PB+PE≥BE,求BE的值即可;
(2)根据题意确定E点的运动轨迹,进而得出BM最大时E点的位置,求出BM即可;
(3)根据费用的关系可知求出线段CF+DF的最小值即可.
【解答】解:(1)以PD为斜边构造30°的直角三角形,且∠PDE=30°,
此时DE=PD,
则PB+PD=PB+PE,
则当P、B、E在同一直线上时PB+PE有最小值为BE,
即PB+PD的最小值为如图①所示PE的长度,
∵AB=1,BC=,
∴BD==2,且∠DBC=30°,
又∵四边形ABCD为矩形,
∴∠BDP=∠DBC=30°,
又∵∠PDE=30°,
∴∠EDB=∠PDE+∠PDE=60°,
∴BE=BD•sin∠EDB=2×sin60°=;
(2)∵E为动点且CE为1,
∴E点的运动轨迹为以C为圆心半径为1的圆,
∵四边形MEBA为正边形,
∴BM=BE,即当BE最大时BM有最大值,
由图②知当E在BC延长线上E'的位置时,BE'有最大值,
此时BE'=BC+CE'=3+1=4,
∴BM=BE'=4,
故BM的最大值为4;
(3)由题知,CD+DF的费用为200CF+100DF=200(CF+DF),
∴求费用的最小值即为求CF+DF的最小值,
连接AC,AF,在AD上截取AD'=10,
∵四边形ABCD是正方形,
∴△ABC是等腰直角三角形,
∵△CEF是等腰直角三角形,
∴∠ACF=∠BCE,==,
∴△ACF∽△BCE,
∴=,
∴AF=BE=20,
可得点F在以A为圆心,AF为半径的弧上,
∵==,∠DAF=∠D'AF,
∴△DAF∽△FAD',
∴=,FD'=DF,
∴CF+DF=CF+FD',
∴当C,F,D'三点共线时CF+DF有最小值为CD',
此时在Rt△CDD'中,CD'===50,
∴铺设CF和DF两条路段的总费用的最小值为200(CF+DF)=200×50=10000(元),
即铺设CF和DF两条路段的总费用的最小值为10000元.
精品解析:2023年陕西省西安市未央区中考数学模拟试卷: 这是一份精品解析:2023年陕西省西安市未央区中考数学模拟试卷,文件包含精品解析2023年陕西省西安市未央区中考数学模拟试卷解析版docx、精品解析2023年陕西省西安市未央区中考数学模拟试卷原卷版docx等2份试卷配套教学资源,其中试卷共31页, 欢迎下载使用。
2023年陕西省西安市未央区西航二中中考数学三模试卷(含答案): 这是一份2023年陕西省西安市未央区西航二中中考数学三模试卷(含答案),共22页。试卷主要包含了单选题,填空题,解答题等内容,欢迎下载使用。
2023年陕西省西安市未央区西航二中中考数学三模试卷: 这是一份2023年陕西省西安市未央区西航二中中考数学三模试卷












