




人教A版 (2019)必修 第二册10.1 随机事件与概率集体备课ppt课件
展开在掷骰子试验中,观察骰子朝上面的点数,可以定义许多随机事件,如:Ci=“点数为i ”,i=1,2,3,4,5,6; D1=“点数不大于3”; D2=“点数大于3”;E1=“点数为1或2”; E2=”点数为2或3“; F=“点数为偶数”; G=“点数为奇数”;你能用集合的形式表示这些事件,借助集合与集合的关系和运算,你能发现这些事件之间的联系吗?
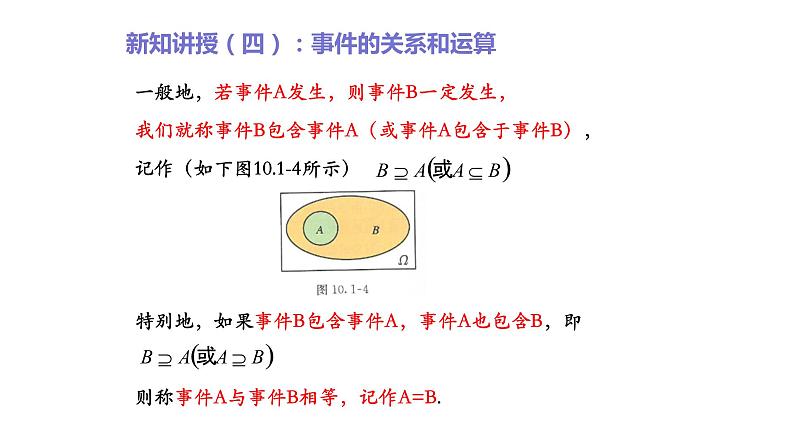
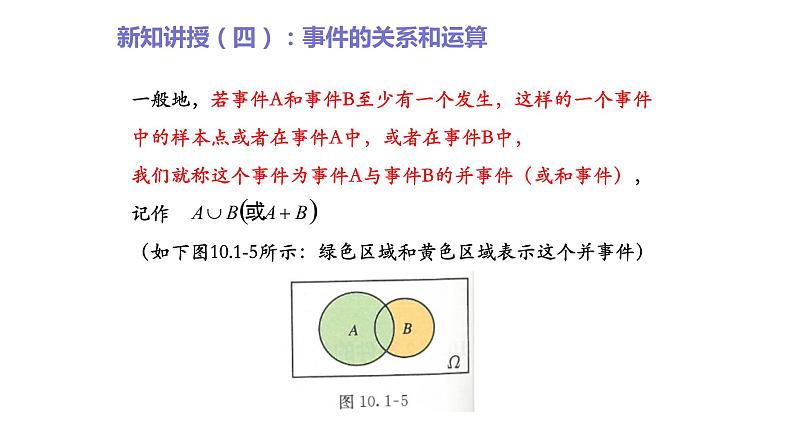
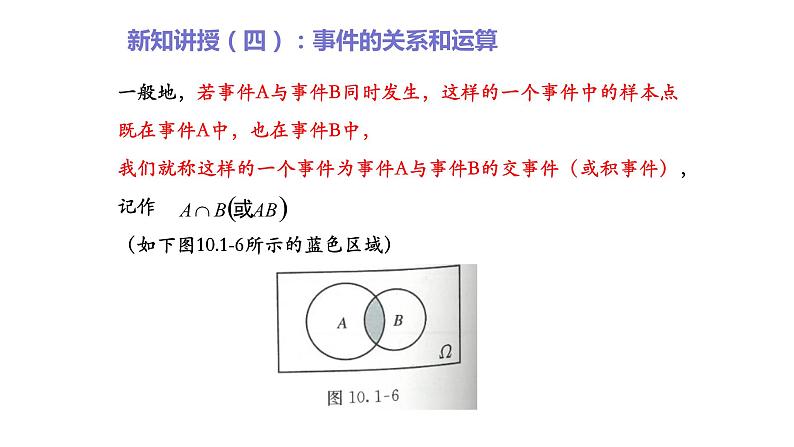
新知讲授(四):事件的关系和运算
思考一:用集合的形式表示事件C1=“点数为1 ”和事件G=“点数为奇数”,借助集合与集合的关系和运算,你能发现这些事件之间的联系吗?由已知得:C1={1}和G={1,3,5}显然,如果事件C1发生,那么事件G一定发生。 用集合表示就是也就是说,事件G包含事件C1.
一般地,若事件A发生,则事件B一定发生,我们就称事件B包含事件A(或事件A包含于事件B),记作(如下图10.1-4所示)特别地,如果事件B包含事件A,事件A也包含B,即 则称事件A与事件B相等,记作A=B.
思考二:用集合的形式表示事件D1=“点数不大于3 ”、事件E1=“点数为1或2”和事件E2=“点数为2或3”,借助集合与集合的关系和运算,你能发现这些事件之间的联系吗?由已知得:D1={1,2,3},E1={1,2}和E2={2,3}显然,事件E1和事件E2至少有一个发生,相当于事件D1发生。用集合表示就是这时我们称事件D1为事件E1和事件E2的并事件。
一般地,若事件A和事件B至少有一个发生,这样的一个事件中的样本点或者在事件A中,或者在事件B中,我们就称这个事件为事件A与事件B的并事件(或和事件),记作 (如下图10.1-5所示:绿色区域和黄色区域表示这个并事件)
思考三:用集合的形式表示事件C2=“点数为2 ”,借助集合与集合的关系和运算,你能发现这些事件之间的联系吗?由已知得:事件E1=“点数为1或2”和事件E2=“点数为2或3”同时发生,相当于事件C2发生。用集合表示就是这时我们称事件C2为事件E1和事件E2的交事件。
一般地,若事件A与事件B同时发生,这样的一个事件中的样本点既在事件A中,也在事件B中,我们就称这样的一个事件为事件A与事件B的交事件(或积事件),记作 (如下图10.1-6所示的蓝色区域)
思考四:用集合的形式表示事件C3=“点数为3 ”和事件C4=“点数为4”,借助集合与集合的关系和运算,你能发现这些事件之间的联系吗?由已知得:事件C3={3},事件C4={4}显然,事件C3与事件C4不可能同时发生。即这时我们称事件C3与事件C4互斥。
一般地,若事件A与事件B不能同时发生,也就是说A∩B是一个不可能事件,即A∩B=Φ我们就称事件A与事件B互斥(或互不相容)(如下图10.1-7所示)
思考五:用集合的形式表示事件F=“点数为偶数 ”和事件G=“点数为奇数”,借助集合与集合的关系和运算,你能发现这些事件之间的联系吗?在任何一次试验中,事件F与事件G两者只能发生其中之一,而且也必然发生其中之一。用集合可以表示为{2,4,6}∪{1,3,5}={1,2,3,4,5,6},即F∪G=Ω,且{2,4,6}∩{1,3,5}=Φ,即F∩G=Φ我们称事件F与事件G互为对立事件。事件D1与D2也有这种关系。
一般地,若事件A和事件B在任何一次试验中有且仅有一个发生,即A∪B=Ω,且A∩B=Φ,我们就称事件A与事件B互为对立。事件A的对立事件记作(如下图10.1-8所示)
思考六:你能根据思考一至思考五,你能总结这些事件之间的关系吗?
A与B有且仅有一个发生
A∪B=Ω,且A∩B=Φ
类似地,我们可以定义多个事件的和事件以及积事件。例如,对于三个事件A,B,C,A∪B∪C(或A+B+C)发生当且仅当A,B,C中至少一个发生,A∩B∩C(或ABC)发生当且仅当A,B,C同时发生,等等。
例5、如图10.1-9,由甲、乙两个元件组成一个并联电路,每个元件可能正常或失效。设事件A=“甲元件正常”,B=“乙元件正常”。(1)写出表示两个元件工作状态的样本空间;(2)用集合的形式表示事件A,B以及它们的对立事件;(3)用集合的形式表示事件A∪B和事件A∩B,并说明它们的含义及关系。
解:(1)用x1,x2分别表示甲、乙两个元件的状态,则可以用(x1,x2)表示这个并联电路的状态。以1表示元件正常,0表示元件失效,则样本空间Ω={(0,0),(0,1),(1,0),(1,1)}(2)根据题意,可得
例6、一个袋子中有大小和质地相同的4个球,其中有2个红色球(标号为1和2),2个绿色球(标号为3和4),从袋中不放回地依次随机摸出2个球。设事件R1=“第一次摸到红球”,R2=“第二次摸到红球”,R=“两次都摸到红球”,G=“两次都摸到绿球”,M=“两个球颜色相同”,N“两个球颜色不同”。(1)用集合的形式分别写出试验的样本空间以及上述各事件;(2)事件R与R1,R与G,M与N之间各有什么关系?(3)事件R与G的并事件与事件M有什么关系?事件R1与R2的交事件与事件R有什么关系?
解:(1)所有的试验结果如图所示。用数组(x1,x2)表示可能的结果,x1是第一次摸到的球的标号,x2是第二次摸到的球的标号,则试验的样本空间Ω={(1,2),(1,3),(1,4),(2,1),(2,3),(2,4),(3,1),(3,2),(3,4),(4,1),(4,2),(4,3)}
事件R1=“第一次摸到红球”,即x1=1或2于是R1={(1,2),(1,3),(1,4),(2,1),(2,2),(2,3)}事件R2=“第二次摸到红球”,即x2=1或2于是R2={(2,1),(3,1),(4,1),(1,2),(3,2),(4,2)}同理,有于是R={(1,2),(2,1)},G={(3,4),(4,3)},M={(1,2),(2,1),(3,4),(4,3)}N={(1,3),(1,4),(2,3),(2,4),(3,1),(3,2),(4,1),(4,2)}
1、在某次考试成绩中(满分为100分),下列事件的关系是什么?① A1={70分~80分},A2={70分以上} ;② B1={不及格},B2={60分以下} ;③ C1={95分以上},C2={90分~95分};④ D1={80分~100分},D2={0分~80分}。①A2包含A1 ②相等③互斥 ④对立
2、判断下面给出的每对事件是否是互斥事件或互为对立事件。从40张扑克牌(四种花色从1~10 各10 张)中任取一张①“抽出红桃”和“抽出黑桃”②“抽出红色牌”和“抽出黑色牌”③“抽出的牌点数为5的倍数”和“抽出的牌点数大于9”①互斥但不对立 ②对立③既不互斥也不对立
3 从40张扑克牌(红桃、黑桃、方块、梅花,点数从1~10各10张)中,任取一张.(1)“抽出红桃”与“抽出黑桃”;(2)“抽出红色牌”与“抽出黑色牌”;(3)“抽出的牌点数为5的倍数”与“抽出的牌点数大于9”.判断上面给出的每对事件是否为互斥事件,是否为对立事件,并说明理由.
解(1)是互斥事件,不是对立事件.理由是:从40张扑克牌中任意抽取1张,“抽出红桃”和“抽出黑桃”是不可能同时发生的,所以是互斥事件.同时,不能保证其中必有一个发生,这是由于还可能抽出“方块”或者“梅花”,因此,二者不是对立事件.(2)既是互斥事件,又是对立事件.理由是:从40张扑克牌中,任意抽取1张,“抽出红色牌”与“抽出黑色牌”,两个事件不可能同时发生,但其中必有一个发生,所以它们既是互斥事件,又是对立事件.
高中数学人教A版 (2019)必修 第二册10.1 随机事件与概率多媒体教学课件ppt: 这是一份高中数学人教A版 (2019)必修 第二册10.1 随机事件与概率多媒体教学课件ppt,共27页。PPT课件主要包含了导入新课,精彩课堂,典例剖析,课堂练习,B∪D∪E,课堂总结等内容,欢迎下载使用。
高中数学人教A版 (2019)必修 第二册第十章 概率10.1 随机事件与概率图文课件ppt: 这是一份高中数学人教A版 (2019)必修 第二册第十章 概率10.1 随机事件与概率图文课件ppt,文件包含核心素养人教版小学数学五年级下册27奇偶性课件pptx、核心素养人教版小学数学五年级下册《奇偶性》教案docxdocx、核心素养人教版小学数学五年级下册27奇偶性导学案docx等3份课件配套教学资源,其中PPT共23页, 欢迎下载使用。
高中数学人教A版 (2019)必修 第二册10.1 随机事件与概率教学课件ppt: 这是一份高中数学人教A版 (2019)必修 第二册10.1 随机事件与概率教学课件ppt,共32页。PPT课件主要包含了学习目标,新知学习,知识点一事件的关系,易错辨析,典例剖析,二事件的运算,随堂小测,课堂小结等内容,欢迎下载使用。













