2021年中考考前最后一卷【重庆A卷】数学

这是一份2021年中考考前最后一卷【重庆A卷】数学，共21页。

1．本试卷共8页，满分150分，考试时间120分钟。
2．考生务必用黑色字迹的签字笔或钢笔在答题卡上填写自己的考号、姓名、试室号、座位号，用2B铅笔把对应该号码的标号涂黑。
3．选择题每小题选出答案后，用2B铅笔把答题卡上对应题目选项的答案信息点涂黑，如需改动，用橡皮擦干净后，再选涂其他答案，答案不能答在试题上。
4．非选择题必须用黑色字迹钢笔或签字笔作答，答案必须写在答题卡各题目指定区域内相应位置上；如需改动，先划掉原来的答案，然后再写上新的答案；不准使用铅笔、涂改液，不按以上要求作答的答案无效。
5．考生务必保持答题卡的整洁，考试结束时，将答题卡交回。
一．选择题（共12小题，满分48分，每小题4分）
1．下列四个数中，最小的数是（ ）
A．5B．0C．﹣3D．﹣4
2．下列几何体中，其俯视图与左视图完全相同的是（ ）
A． B． C． D．
3．习近平总书记提出了五年“精准扶贫”的战略构想，意味着每年要减贫约11600000人，将数据11600000用科学记数法表示为（ ）
A．1.16×106B．1.16×107C．1.16×108D．11.6×106
4．如图，AB∥CD，∠A＝100°，∠BCD＝50°，∠ACB的度数为（ ）
A．25°B．30°C．45°D．50°
5．估计的值在（ ）
A．2和3之间B．3和4之间C．4和5之间D．5和6之间
6．若一个正多边形的每一个外角都等于40°，则这个正多边形的边数是（ ）
A．7B．8C．9D．10
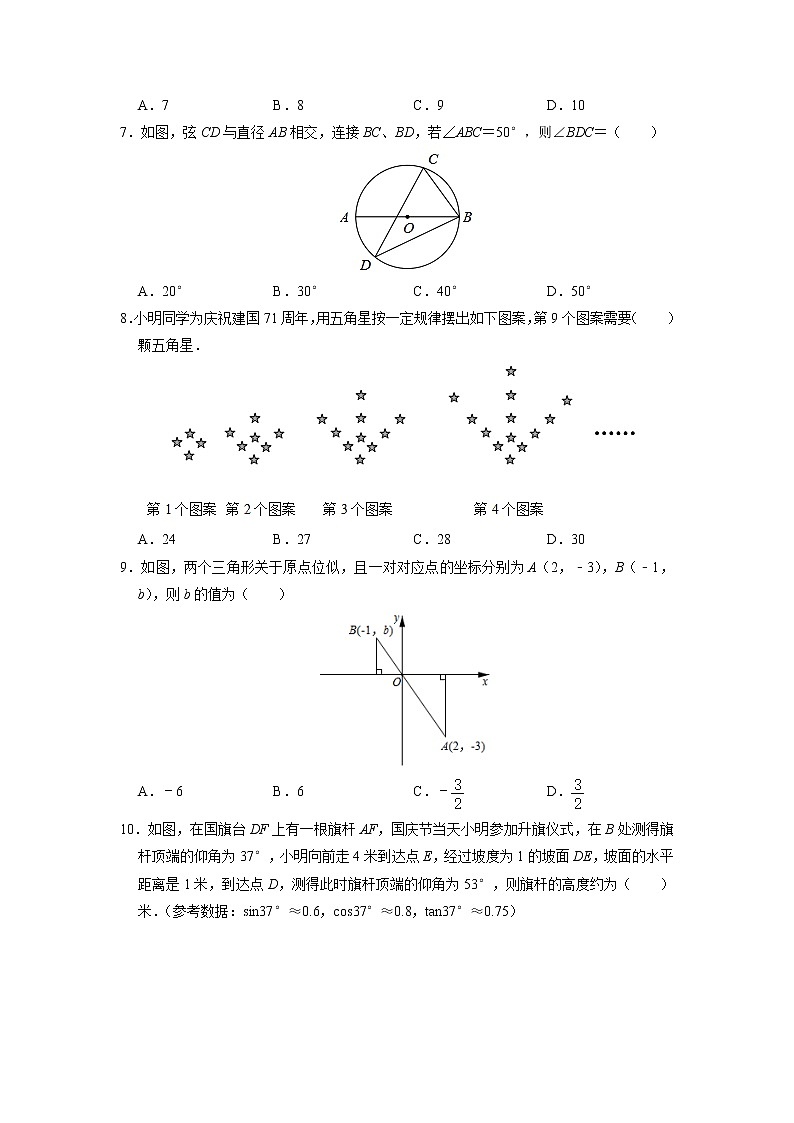
7．如图，弦CD与直径AB相交，连接BC、BD，若∠ABC＝50°，则∠BDC＝（ ）
A．20°B．30°C．40°D．50°
8．小明同学为庆祝建国71周年，用五角星按一定规律摆出如下图案，第9个图案需要（ ）颗五角星．
A．24B．27C．28D．30
9．如图，两个三角形关于原点位似，且一对对应点的坐标分别为A（2，﹣3），B（﹣1，b），则b的值为（ ）
A．﹣6B．6C．﹣D．
10．如图，在国旗台DF上有一根旗杆AF，国庆节当天小明参加升旗仪式，在B处测得旗杆顶端的仰角为37°，小明向前走4米到达点E，经过坡度为1的坡面DE，坡面的水平距离是1米，到达点D，测得此时旗杆顶端的仰角为53°，则旗杆的高度约为（ ）米．（参考数据：sin37°≈0.6，cs37°≈0.8，tan37°≈0.75）
A．6.29B．4.71C．4D．5.33
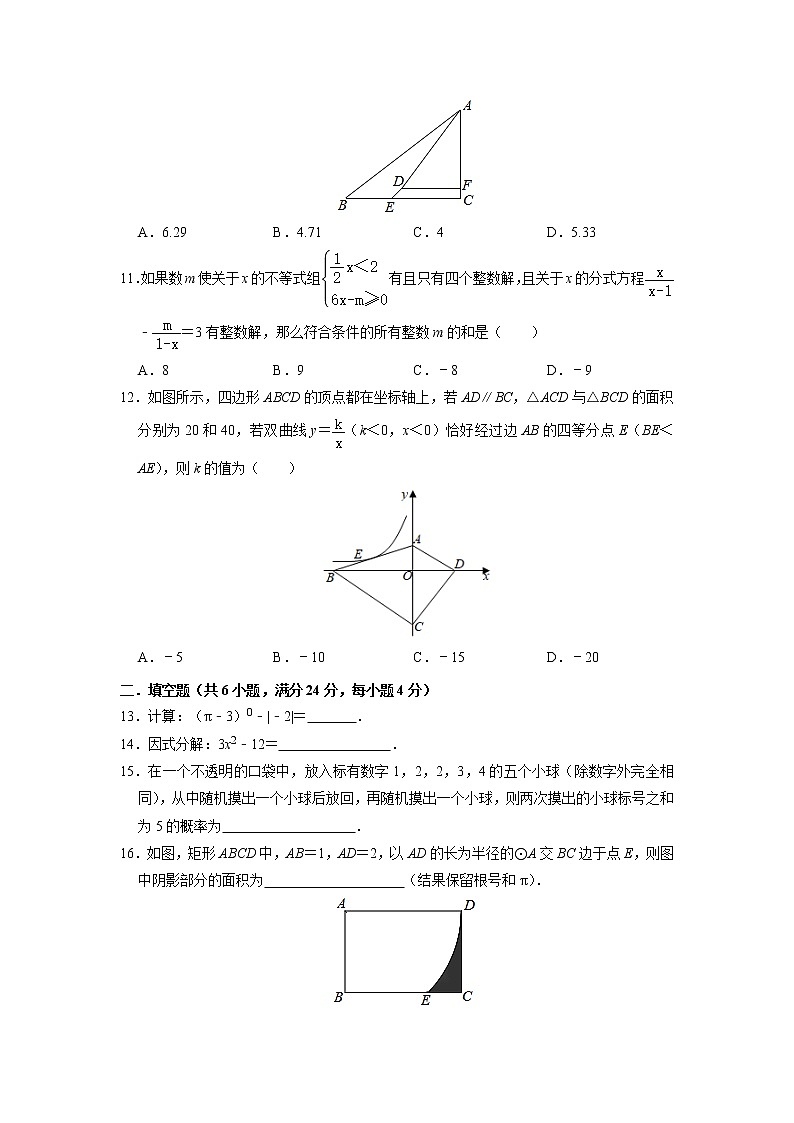
11．如果数m使关于x的不等式组有且只有四个整数解，且关于x的分式方程﹣＝3有整数解，那么符合条件的所有整数m的和是（ ）
A．8B．9C．﹣8D．﹣9
12．如图所示，四边形ABCD的顶点都在坐标轴上，若AD∥BC，△ACD与△BCD的面积分别为20和40，若双曲线y＝（k＜0，x＜0）恰好经过边AB的四等分点E（BE＜AE），则k的值为（ ）
A．﹣5B．﹣10C．﹣15D．﹣20
二．填空题（共6小题，满分24分，每小题4分）
13．计算：（π﹣3）0﹣|﹣2|＝ ．
14．因式分解：3x2﹣12＝ ．
15．在一个不透明的口袋中，放入标有数字1，2，2，3，4的五个小球（除数字外完全相同），从中随机摸出一个小球后放回，再随机摸出一个小球，则两次摸出的小球标号之和为5的概率为 ．
16．如图，矩形ABCD中，AB＝1，AD＝2，以AD的长为半径的⊙A交BC边于点E，则图中阴影部分的面积为 （结果保留根号和π）．
17．小宁和弟弟小强分别从家和图书馆出发，沿同一条笔直的马路相向而行，小宁先出发5分钟后，小强骑自行车匀速回家，小宁开始跑步中途改为步行，且步行的速度为跑步速度的一半，到达图书馆恰好用了35分钟，两人之间的距离y（m）与小宁离开出发地的时间x（min）之间的函数图象如图所示，则当弟弟到家时，小宁离图书馆的距离为 米．
18．2021新春佳节之际，某商家推出收费印制巴蜀中学lg的新春礼品，礼品主要包含三种：对联，门神和红包，如果印制对联3副、门神2副、红包5个，需付人民币31.5元；如果印制对联2副、门神1副、红包1个，需付人民币22元，某人想印制16副对联、10副门神、22个红包共需付人民币 元．
三．解答题（本大题7个小题，每小题10分，共70分）
19．（10分）计算：
（1）（2a﹣b）2+（a+b）（a﹣b）；
（2）（1﹣）÷．
20．（10分）如图，AE∥BF，AC平分∠BAD，且交BF于点C，BD平分∠ABC，且与AE交于点D，连接CD．
（1）求证：四边形ABCD是菱形；
（2）若AC＝6，BD＝8，AM⊥BC于M，求AM的长．
21．（10分）某防护服生产公司旗下有A、B两个生产车间，为了解A、B两个生产车间工人的日均生产数量，公司领导小组从A、B两个生产车间分别随机抽取了20名工人的日均生产数量x（单位：套），并对数据进行分析整理（数据分为五组：A.25≤x＜35，B.35≤x＜45，C.45≤x＜55，D.55≤x＜65，E.65≤x＜75）．得出了以下部分信息：
A．B两个生产车间工人日均生产数量的平均数、中位数、众数、极差如表：
“B生产车间”工人日均生产数量在C组中的数据是：52，45，54，48，54，其余所有数据的和为807．
根据以上信息，回答下列问题：
（1）上述统计图表中，a＝ ，b＝ ．扇形统计图B组所对应扇形的圆心角度数为 °．
（2）根据以上数据，你认为哪个生产车间情况更好？请说明理由（一条理由即可）；
（3）若A生产车间共有200名工人，B生产车间共有180个工人，请估计该公司生产防护服数量在“45≤x＜65”范围的工人数量．
22．（10分）一个正整数，若从左到右奇数位上的数字相同，偶数位上的数字相同，称这样的数为“接龙数”．例如：121，3535都是“接龙数”，123不是“接龙数”．
（1）求证：任意四位“接龙数”都能被101整除；
（2）若一个数能表示成某个整数的平方的形式，则称这个数为完全平方数．对于任意的三位“接龙数”，记F（t）＝﹣2﹣x，求使得F（t）为完全平方数的所有三位“接龙数”．
23．（10分）“过雨荷花满院香，沉李浮瓜冰雪凉”，炎热的夏季正是各种水果大量上市的季节，香果园大型水果超市的江安李子和山东烟台的红富士苹果很受消费者的欢迎，苹果售价24元/千克，李子售价16元/千克．
（1）若第一周苹果的平均销量比李子的平均销量多200千克，且这两种水果的总销售额为12800元，则第一周销售苹果多少千克？
（2）该水果超市第一周按照（1）中苹果和李子的销量销售这两种水果，并决定第二周继续销售这两种水果，第二周苹果售价降低了a%，销量比第一周增加了a%，李子的售价保持不变，销量比第一周增加了a%，结果这两种水果第二周的总销售额比第一周增加了a%，求a的值．
24．（10分）小南根据学习函数的经验，对函数y＝a|x﹣2|+b的图象与性质进行了探究．下表是小南探究过程中的部分信息：
请按要求完成下列各小题：
（1）该函数的解析式为 ，自变量x的取值范围为 ；
（2）n的值为 ；点（，﹣） 该函数图象上；（填“在”或“不在”）
（3）在如图所示的平面直角坐标系中，描全上表中以各对对应值为坐标的点，并画出该函数的图象；
（4）结合函数的图象，解决问题：
①写出该函数的一条性质： ；
②如图，在同一坐标系中是一次函数y＝﹣x+的图象，根据图象回答，当a|x﹣2|+b＜﹣x+时，自变量x的取值范围为 ．
25．（10分）如图，抛物线y＝ax2+bx+8（a≠0）与x轴交于点A（﹣2，0）和点B（8，0），与y轴交于点C，顶点为D，连接AC，BC，BC与抛物线的对称轴l交于点E．
（1）求抛物线的表达式；
（2）点P是第一象限内抛物线上的动点，连接PB，PC，当S△PBC＝S△ABC时，求点P的坐标；
（3）点N是对称轴l右侧抛物线上的动点，在射线ED上是否存在点M，使得以点M，N，E为顶点的三角形与△OBC相似？若存在，求点M的坐标；若不存在，请说明理由．
四、解答题（本大题1个小题，共8分）
26．（8分）在△ABC中，AB＝AC＝6，∠BAC＝90°，AD⊥BC于点D，E为线段AD上的一点，AE：DE＝2：1，以AE为直角边在直线AD右侧构造等腰Rt△AEF，使∠EAF＝90°，连接CE，G为CE的中点．
（1）如图1，EF与AC交于点H，连接GH，求线段GH的长度．
（2）如图2，将△AEF绕点A逆时针旋转，旋转角为α且45°＜α＜135°，H为线段EF的中点，连接DG，HG，猜想∠DGH的大小是否为定值，并证明你的结论；
（3）如图3，连接BG，将△AEF绕点A逆时针旋转，在旋转过程中，请直接写出BG长度的最大值．
1．【解答】解：∵|﹣3|＝3，|﹣4|＝4，
∴﹣3＞﹣4，
∴5＞0＞﹣3＞﹣4，
∴最小的数是﹣4．
故选：D．
2．【解答】解：A、俯视图是带圆心的圆，左视图是等腰三角形，故本选项不合题意；
B、俯视图是矩形，左视图是圆，故本选项不合题意；
C、俯视图与左视图都是正方形，故本选项符合题意；
D、俯视图是三角形，左视图是矩形，故本选项不合题意；
故选：C．
3．【解答】解：11600000＝1.16×107．
故选：B．
4．【解答】解：∵AB∥CD，∠A＝100°．
∴∠A+∠ACD＝180°．
∴∠ACD＝80°．
∵∠BCD＝50°．
∴∠ACB＝∠ACD﹣BCD＝30°．
故选：B．
5．【解答】解：∵5＜＜6，
∴的值在5和6之间．
故选：D．
6．【解答】解：∵360÷40＝9，
∴这个多边形的边数是9．
故选：C．
7．【解答】解：连接AC，如图所示：
∵AB是圆O的直径，
∴∠ACB＝90°，
∴∠A+∠ABC＝90°，
∴∠A＝90°﹣∠ABC＝90°﹣50°＝40°，
∴∠BDC＝∠A＝40°；
故选：C．
8．【解答】解：设第n个图案需要an（n为正整数）颗五角星．
观察图形，可知：a1＝3×1+1，a2＝3×2+1，a3＝3×3+1，…，
∴an＝3n+1，
∴a9＝3×9+1＝28．
故选：C．
9．【解答】解：∵两三角形关于原点位似，
∴＝，解得b＝．
故选：D．
10．【解答】解：过点D作DM⊥BC，垂足为M，由题意得，
∠B＝37°，∠ADF＝53°，BE＝4，EM＝1，
∵坡面DE的坡度为1，
∴＝1，
∴DM＝EM＝1＝FC，
在Rt△ADF中，∠DAF＝90°﹣∠ADF＝90°﹣53°＝37°，
∵tan∠DAF＝≈0.75，
设AF＝x，则DF＝0.75x＝MC，
在Rt△ABC中，
∵tan∠B＝，
∴tan37°＝≈0.75，
解得x＝≈6.29（米），
故选：A．
11．【解答】解：﹣＝3，
分式方程去分母得：x+m＝3（x﹣1），
解得：x＝，
﹣1≠0，解得m≠﹣1，
解不等式组得：≤x＜4，
由不等式组有且只有四个整数解，得到﹣1＜≤0，
解得：﹣6＜m≤0，
由x为整数，且﹣1≠0，
解得：m＝﹣5或﹣3，
则符合条件的所有整数m的和是﹣5﹣3＝﹣8．
故选：C．
12．【解答】解：∵AD∥BC，
∴S△BCD＝S△BCA，S△ACD＝S△ABD．
∵△ACD与△BCD的面积分别为20和40，
∴△ABD和△BCD面积比为1：2，
∴根据同底得：AO：OC＝DO：OB＝1：2，
∴S△AOB＝S△ABD＝．
∵双曲线y＝（k＜0，x＜0）恰好经过边AB的四等分点E（BE＜AE），
∴S△AOB+|k|+S△AOB＝S△AOB，
∴|k|＝S△AOB＝×＝5，
∵双曲线经过第二象限，k＜0，
∴k＝﹣5．
故选：A．
二．填空题（共6小题，满分24分，每小题4分）
13．【解答】解：原式＝1﹣2＝﹣1，
故答案为：﹣1．
14．【解答】解：原式＝3（x2﹣4）
＝3（x+2）（x﹣2）．
故答案为：3（x+2）（x﹣2）．
15．【解答】解：列表如下：
由表知，共有25种等可能结果，其中两次摸出的小球标号之和为5的有6种结果，
所以两次摸出的小球标号之和为5的概率为，
故答案为：．
16．【解答】解：连接AE，
∵四边形ABCD是矩形，AB＝1，AD＝2，AD＝AE，
∴∠BAD＝∠B＝90°，AE＝2，
∴sin∠AEB＝＝，BE＝＝，
∴∠AEB＝30°，
∴∠BAE＝60°，
∴∠EAD＝∠BAD﹣∠BAE＝30°，
∴阴影部分的面积是：2×1﹣﹣＝2﹣﹣，
故答案为：2﹣﹣．
17．【解答】解：由图可得，
小宁跑步的速度为：（4500﹣3500）÷5＝200m/min，则步行速度为：200×＝100m/min，
设小宁由跑步变为步行的时刻为a分钟，
200a+（35﹣a）×100＝4500，
解得，a＝10，
设小强骑车速度为xm/min，
200（10﹣5）+（10﹣5）x＝3500﹣1000，
解得，x＝300，
即小强骑车速度为300m/min，
小强到家用的时间为：4500÷300＝15min，
则当弟弟小强到家时，小宁离图书馆的距离为：4500﹣10×200﹣（5+15﹣10）×100＝1500m，
故答案为：1500．
18．【解答】解：设印制1副对联需要x元，1副门神需要y元，1个红包需要z元，
依题意得：，
①×4+②×2得：16x+10y+22z＝170．
故答案为：170．
三．解答题（共7小题，满分70分）
19．【解答】解：（1）原式＝4a2﹣4ab+b2+a2﹣b2
＝5a2﹣4ab；
（2）原式＝•
＝•
＝．
20．【解答】（1）证明：∵AE∥BF，
∴∠ADB＝∠DBC，∠DAC＝∠BCA，
∵AC、BD分别是∠BAD、∠ABC的平分线，
∴∠DAC＝∠BAC，∠ABD＝∠DBC，
∴∠BAC＝∠ACB，∠ABD＝∠ADB，
∴AB＝BC，AB＝AD，
∴AD＝BC，
∵AD∥BC，
∴四边形ABCD是平行四边形，
∵AD＝AB，
∴四边形ABCD是菱形；
（2）解：∵四边形ABCD是菱形，
∴AC⊥BD，AO＝AC＝3，BO＝BD＝4，
∴AB＝＝＝5，
∴BC＝AB＝5，
∴BC•AM＝AC•BD，
即5AM＝×6×8，
∴AM＝．
21．【解答】解：（1）“B生产车间”工人日均生产数量在C组中的数据是：52，45，54，48，54，
因此“C组”所占的百分比为5÷20＝25%，“B组”所占的百分比为1﹣25%﹣10%﹣15%﹣30%＝20%，
所以“A组”的频数为：20×10%＝2（人），
“B组”的频数为：20×20%＝4（人），
“C组”的频数为：20×25%＝5（人），
“D组”的频数为：20×30%＝6（人），
“E组”的频数为：20×15%＝3（人），
因此“B车间”20名工人，日生产数量从小到大排列，处在中间位置的两个数的都是54，
所以中位数是54，
即b＝54，
“B车间”20名工人，日生产数量的平均数为：30×10%+40×20%+50×25%+60×30%+70×15%＝53，
即a＝53，
360°×20%＝72°，
故答案为：53，54，72；
（2）“A车间”的生产情况较好，理由：“A车间”工人日均生产量的平均数，中位数均比“B车间”的高；
（3）200×+180×（25%+30%）＝199（人），
答：A生产车间200人，B生产车间180人，估计生产防护服数量在“45≤x＜65”范围的工人大约有199人．
22．【解答】解：（1）设四位“接龙数”为（0＜a≤9，0≤b≤9，且a，b为整数）
∴＝1000a+100b+10a+b＝1010a+101b＝101（10a+b），
∵a，b为正整数，
∴10a+b是正整数，
∴能被101整除，
即任意四位“接龙数”都能被101整除；
（2）∵F（t）＝﹣2﹣x
＝100x+10y+x﹣2（10x+y）﹣x
＝80x+8y
＝22×2（10x+y），
∵0＜x≤9，0≤y≤9，且x，y均为整数，
∴10＜10x+y＜100，
∴20＜2（10x+y）＜200，2（10x+y）是偶数，
∵F（t）为完全平方数，
∴2（10x+y）＝36或64或100或144或196，
∴10x+y＝18或32或50或72或98，
∴x＝1，y＝8或x＝3，y＝2或x＝5，y＝0或x＝7，y＝2或x＝9，y＝8；
∴使得F（t）为完全平方数的所有三位“接龙数”为181或323或505或727或989．
23．【解答】解：（1）设第一周李子销售量为x千克．则苹果的平均销量为y千克，
根据题意得：，
解得：，
答：第一周销售苹果400千克；
（2）根据题意得：24（1﹣a%）×400（1+a%）+16×200（1+a%）＝12800（1+a%），
∴a1＝60，a2＝0（舍去）．
答：a的值为60．
24．【解答】解：（1）把点（﹣1，0）和（0，﹣1）代入y＝a|x﹣2|+b得，
解得，
∴该函数的解析式为y＝|x﹣2|﹣3，自变量x的取值范围为x是任意实数；
故答案为y＝|x﹣2|﹣3，x是任意实数；
（2）把x＝2代入y＝|x﹣2|﹣3得，y＝﹣3，
∴n＝﹣3；
把x＝代入y＝|x﹣2|﹣3得，y＝﹣≠﹣，
∴点（，﹣） 不在该函数图象上；
故答案为﹣3，不在；
（3）画出函数图象如图：
（4）结合函数的图象，
①写出该函数的一条性质：函数有最小值﹣3；
故答案为函数有最小值﹣3；
②如图，在同一坐标系中是一次函数y＝﹣x+的图象，根据图象可知，当a|x﹣2|+b＜﹣x+时，自变量x的取值范围为﹣2＜x＜4，
故答案为﹣2＜x＜4．
25．【解答】解：（1）∵抛物线y＝ax2+bx+8（a≠0）过点A（﹣2，0）和点B（8，0），
∴，
解得．
∴抛物线解析式为：；
（2）当x＝0时，y＝8，
∴C（0，8），
∴直线BC解析式为：y＝﹣x+8，
∵，
∴，
过点P作PG⊥x轴，交x轴于点G，交BC于点F，
设，
∴F（t，﹣t+8），
∴，
∴，
即，
∴t1＝2，t2＝6，
∴P1（2，12），P2（6，8）；
（3）∵C（0，8），B（8，0），∠COB＝90°，
∴△OBC为等腰直角三角形，
抛物线的对称轴为，
∴点E的横坐标为3，
又∵点E在直线BC上，
∴点E的纵坐标为5，
∴E（3，5），
设，
①当MN＝EM，∠EMN＝90°，
△NME～△COB，则，
解得或（舍去），
∴此时点M的坐标为（3，8），
②当ME＝EN，当∠MEN＝90°时，
则，
解得：或（舍去），
∴此时点M的坐标为；
③当MN＝EN，∠MNE＝90°时，
此时△MNE与△COB相似，
此时的点M与点E关于①的结果（3，8）对称，
设M（3，m），
则m﹣8＝8﹣5，
解得m＝11，
∴M（3，11）；
此时点M的坐标为（3，11）；
故在射线ED上存在点M，使得以点M，N，E为顶点的三角形与△OBC相似，点M的坐标为：（3，8），或（3，11）．
四、解答题（8分）
26．【解答】解：（1）如图1中，连接BE，CF．
∵AB＝AC＝6，∠BAC＝90°，AD⊥BC于点D，
∴BC＝AB＝12，BD＝CD＝6，∠BAD＝∠CAD＝30°，
∴AD＝BD＝DC＝6，
∵△AEF是等腰直角三角形，
∴AE＝AF
∵∠DAH＝∠FAH＝45°，
∴EH＝HF，
∵AE：DE＝2：1，
∴AE＝4，DE＝2，
∴BE＝＝＝2，
∵AB＝AC，AE＝AF，∠BAC＝∠EAF＝90°，
∴∠BAE＝∠CAF，
∴△BAE≌△CAF（SAS），
∴CF＝BE＝2，
∵EG＝CG，EH＝FH，
∴GH＝CF＝．
（2）结论：∠DGH＝90°是定值．
理由：连接BE，CF，设CF交BE于点O，BE交AC于J．同法可证△BAE≌△CAF（SAS），
∴∠ABE＝∠ACF，
∵∠AJB＝∠CJO，
∴∠COJ＝∠BAJ＝90°，
∴CF⊥BE，
∵EH＝HF，EG＝GC，
∴GH∥CF，
∵CD＝DB，CG＝GE，
∴DG∥BE，
∴DG⊥GH，
∴∠DGH＝90°．
（3）如图3中，取AC的中点J，连接BJ，JG．
由题意AJ＝JC＝3，AB＝6，
∵∠BAJ＝90°，
∴BJ＝＝＝3，
∵AJ＝JC，EG＝CG，
∴JG＝AE＝2，
∵BG≤BJ+JG，
∴BG≤3+2，
∴BG的最大值为3+2车间
平均数（个）
中位数（个）
众数（个）
极差
A
54
56
62
42
B
a
b
64
45
x
…
﹣4
﹣3
﹣2
﹣1
0
1
2
3
4
…
y
…
3
2
1
0
﹣1
﹣2
n
﹣2
﹣1
…
1
2
2
3
4
1
2
3
3
4
5
2
3
4
4
5
6
2
3
4
4
5
6
3
4
5
5
6
7
4
5
6
6
7
8