






数学九年级上册25.2 用列举法求概率精品ppt课件
展开一般地,如果在一次试验中,有n种可能的结果,并且它们发生的可能性都相等,事件A包含其中的m种结果,那么事件A发生的概率为:
1.知道“直接列举法”和“列表法”求随机事件的概率的适用条件.
2.会正确“列表”表示出所有可能出现的结果.
3.知道如何利用“列表法”求随机事件的概率.
同时抛掷两枚质地均匀的硬币,求下列事件的概率:(1) 两枚硬币全部正面向上;(2) 两枚硬币全部反面向上;(3) 一枚硬币正面向上、一枚硬币反面向上.
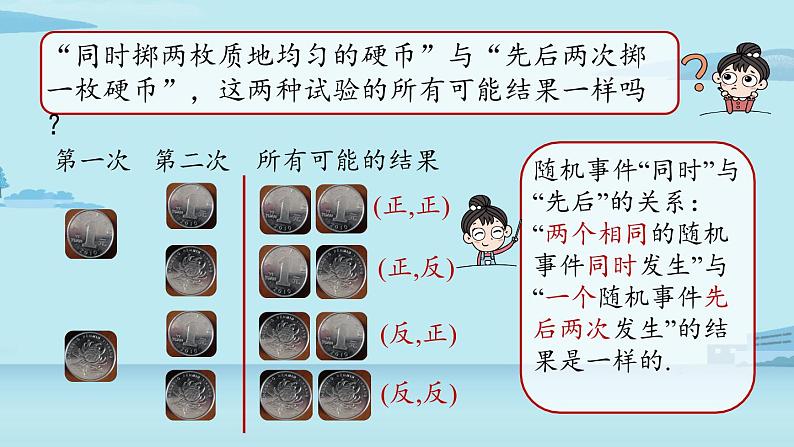
分析:“掷两枚硬币”所有结果如下.
解:列举抛掷两枚硬币所能产生的所有结果,它们是:
(1)其中两枚硬币全部正面向上(记为事件A)的结果有1种,即“正正”,所以
(2) 两枚硬币全部反面向上(记为事件B)的结果有1种,即“正反”,所以
(3)一枚硬币正面向上、一枚硬币反面向上(记为事件C) 的结果共有两种,即“反正”“正反”所以
技巧点拨:先列出硬币落地后所有可能出现的结果,再分别数出各种事件发生的结果数,最后带入概率公式求解。
正正,正反,反正,反反.
只需比较老师赢和学生赢的概率是否一样就可以了.
同时向空中抛掷两枚质地均匀的硬币,若落地后一正一反,老师赢;若落地后两面一样,学生赢. 那么这个游戏公平吗?
注意:(1)为保证结果不重不漏,直接列举时,要有一定的顺序性. (2)用列举法求概率的前提条件有两个: ①所有可能出现的结果是有限个; ②每个结果出现的可能性相等. (3)所求概率是一个准确数,一般用分数表示.
例1 若我们把十位上的数字比个位和百位上数字都小的三位数称为“V数”, 如756, 326 , 那么从2, 3, 4这三个数字组成的无重复数字的三位数中任意抽取一个数, 则该数是“V数”的概率为 .
分析:求解本题的关键是不重不漏地列举出由2,3,4组成的无重复数字的所有的三位数.
同时掷两枚质地均匀的骰子,计算下列事件的概率:(1)两枚骰子的点数相同;(2)两枚骰子点数的和是9;(3)至少有一枚骰子的点数为2.
解:两枚骰子分别记为第1枚和第2枚,可以用下表列举出所有可能出现的结果.
(1)记两枚骰子的点数相同为事件A.
(2)记两枚骰子的点数的和是9为事件B.
(3)记至少有一枚骰子的点数为2为事件C.
共有36种等可能的结果
当一次试验涉及两个因素,并且可能出现的等可能结果数目较多时,为不重不漏地列出所有等可能的结果,通常采用列表法。
②通过表格确定公式中m, n的值
③利用P(A)= 计算事件的概率
运用列表法求概率的步骤
一个因素所包含的可能情况
另一个因素所包含的可能情况
两个因素所组合的所有可能情况
列表法中表格构造特点:
例2 利用如图所示的两个转盘玩配紫色游戏(红色和蓝色可以配成紫色),两个转盘各转一次,则指针所指区域可以配成紫色的概率为多少?
2.一个不透明的袋中有四个完全相同的小球,把它们分别标号为1,2,3,4.随机地摸取一个小球然后放回,再随机地摸出一个小球.求下列事件的概率:(1)两次取出的小球标号相同;(2)两次取出的小球标号和等于4.
解:(1)记两次取出的小球标号 相同为事件A.
(2)记两次取出的小球标号和等于4为事件B.
1.把一副普通扑克牌中的13张黑桃牌洗匀后正面向下放在桌子上,从中随机抽取一张,求下列事件的概率:(1) 抽出的牌是黑桃6;(2) 抽出的牌是黑桃10;(3) 抽出的牌带有人像;(4) 抽出的牌上的数小于5;(5) 抽出的牌的花色是黑桃.
2.不透明袋子中装有红、绿小球各一个,除颜色外无其他差别.随机摸出一个小球后,放回并摇匀,再随机摸出一个.求下列事件的概率:(1) 第一次摸到红球,第二次摸到绿球;(2) 两次都摸到相同颜色的小球;(3) 两次摸到的小球中一个绿球、一个红球.
3.五张形状、大小、背面完全相同的卡片上分别标有数-3,-1,0,1,2,将卡片洗匀后背面朝上放在桌面上,从中任意抽取两张,则所抽卡片上的数的积是正数的概率是多少?
为什么对角线上的数据没列出来呢?
积是正数: 种
P(所抽卡片上的数的积是正数) =
易错警示:混淆“放回”与“不放回”致错本题是不放回试验,不可能抽到两张数相同的卡片,所以列表格里要排除掉两张卡片上的数相同的情况.
两个试验因素或分两步进行的试验.
① 列表;② 确定m,n的值; ③代入概率公式计算.
正确列举出所有等可能出现的结果.
确保试验中每种结果出现的可能性大小相等.
A. B. C. D.
1.(2020•北京中考)不透明的袋子中有两个小球,上面分别写着数字“1”,“2”,除数字外两个小球无其他差别.从中随机摸出一个小球,记录其数字,放回并摇匀,再从中随机摸出一个小球,记录其数字,那么两次记录的数字之和为3的概率是( )
由表可知,共有4种等可能的结果,其中两次记录的数字之和为3的有2种结果,所以两次记录的数字之和为3的概率为
2.有6张看上去无差别的卡片,上面分别写着1, 2, 3, 4, 5, 6.随机抽取1张后,放回并混在一起,再随机抽取1张,那么第二次取出的数字能够整除第一次取出的数字的概率是多少?
解:由题意得两次抽取共有36种等可能出现的结果,第二次取出的数字能够整除第一次取出的数字的结果有14种,即有(1,1), (2,1), (2,2), (3,1), (3,3), (4,1), (4,2), (4,4),(5,1),(5,5),(6,1),(6,2),(6,3),(6,6) ,所以所求概率为 .
3.一个不透明的口袋中有四个完全相同的小球,把它们分别标号为1,2,3,4,随机摸出一个小球然后放回,再随机摸出一个小球,求下列事件的概率.两次摸出的小球的标号相同;(2) 两次摸出的小球标号的和等于4.
初中数学人教版九年级上册25.2 用列举法求概率一等奖课件ppt: 这是一份初中数学人教版九年级上册25.2 用列举法求概率一等奖课件ppt,共24页。PPT课件主要包含了用列举法求概率,列表法,第1枚,第2枚,第1次,第2次,∵P和为4≠,P和为5等内容,欢迎下载使用。
初中数学人教版九年级上册25.2 用列举法求概率教课内容课件ppt: 这是一份初中数学人教版九年级上册25.2 用列举法求概率教课内容课件ppt,共17页。PPT课件主要包含了课件说明,复习旧知,探究新知,第1枚,第2枚,列表法,运用新知,巩固新知,课堂小结等内容,欢迎下载使用。
初中数学25.2 用列举法求概率教案配套课件ppt: 这是一份初中数学25.2 用列举法求概率教案配套课件ppt,文件包含精选备课2021秋人教版数学九年级上册252用列举法求概率第1课时课件pptx、精选备课2021秋人教版数学九年级上册252用列举法求概率第1课时学案docx、精选备课2021秋人教版数学九年级上册252用列举法求概率第1课时教学设计docx、精选备课2021秋人教版数学九年级上册252用列举法求概率第1课时练习docx等4份课件配套教学资源,其中PPT共33页, 欢迎下载使用。













