浙江省湖州市2020-2021学年八年级下学期期中数学试卷

这是一份浙江省湖州市2020-2021学年八年级下学期期中数学试卷，共5页。试卷主要包含了下列等式，已知一组数据等内容，欢迎下载使用。

1．下列常用手机APP的图标中，是中心对称图形的是（ ）
A．B．C．D．
2．若代数式在实数范围内有意义，则x的取值范围是（ ）
A．x≥﹣2B．x＞﹣2C．x≥2D．x＞2
3．用配方法解方程2x2﹣x﹣1＝0，变形结果正确的是（ ）
A．（x﹣）2＝B．（x﹣）2＝
C．（x﹣）2＝D．（x﹣）2＝
4．下列等式：①＝，②＝﹣2，③＝﹣2，④，⑤＝±4，⑥﹣，正确的有（ ）个
A．5个B．4个C．3个D．2个
5．已知一组数据：2，5，5，6，7，则这组数据的方差是（ ）
A．2.6B．2.8C．3D．3.2
6．已知a为整数，且＜a＜，则整数a有（ ）
A．1个B．2个C．3个D．4个
7．用反证法证明命题“在直角三角形中，至少有一个锐角不大于45°”，应先假设（ ）
A．两个锐角都小于45°
B．两个锐角都大于45°
C．一个锐角小于45°
D．一个锐角小于或等于45°
8．某种商品原价是100元，经两次降价后的价格是90元．设平均每次降价的百分率为x，可列方程为（ ）
A．100（1+2x）＝90B．100（1﹣2x）＝90
C．100（1+x）2＝90D．100（1﹣x）2＝90
9．关于x的一元二次方程ax2+bx+c＝0（a≠0），下列命题：
①若a、c异号，则方程ax2+bx+c＝0必有两个不相等的实数根；
②若4a﹣2b+c＝0，则方ax2+bx+c＝0有一个根为﹣2；
③若方程ax2+bx+c＝0的两根互为相反数，则b＝0；
④若b＝a+c，则ax2+bx+c＝0方程有两个不相等的实数根．
其中真命题为（ ）
A．①②④B．①②③C．②③④D．①③④
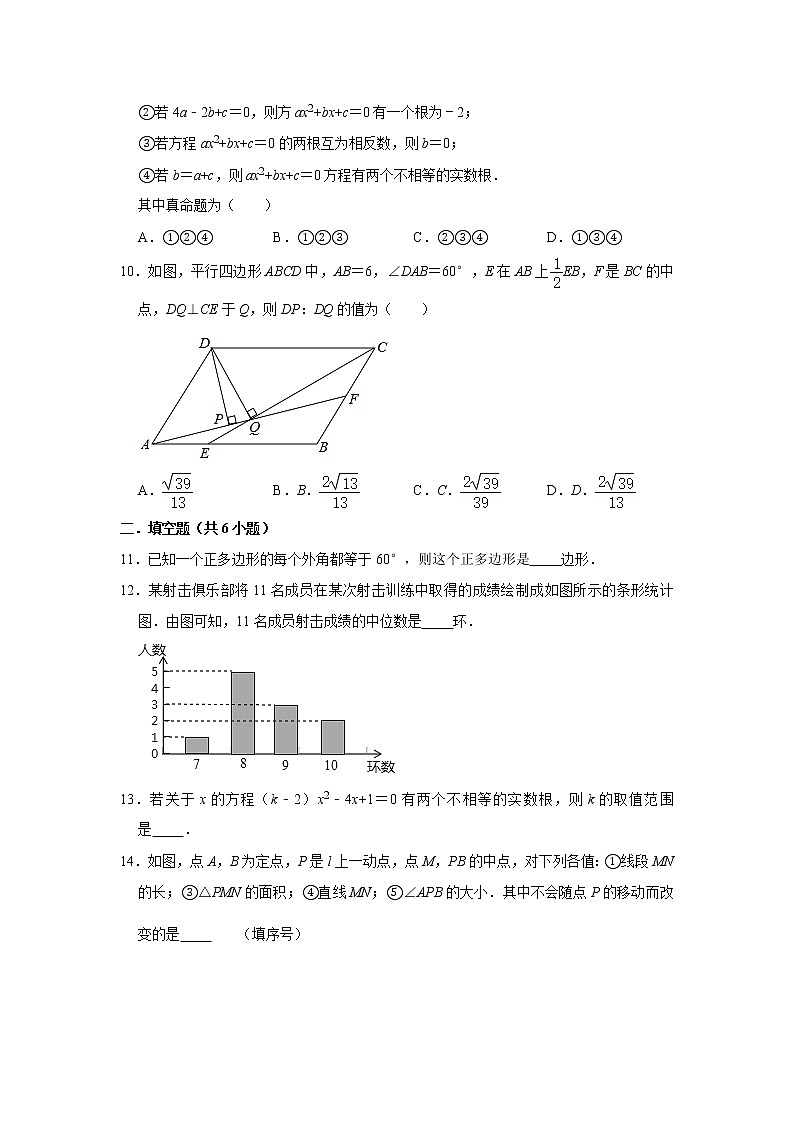
10．如图，平行四边形ABCD中，AB＝6，∠DAB＝60°，E在AB上EB，F是BC的中点，DQ⊥CE于Q，则DP：DQ的值为（ ）
A．B．B．C．C．D．D．
二．填空题（共6小题）
11．已知一个正多边形的每个外角都等于60°，则这个正多边形是 边形．
12．某射击俱乐部将11名成员在某次射击训练中取得的成绩绘制成如图所示的条形统计图．由图可知，11名成员射击成绩的中位数是 环．
13．若关于x的方程（k﹣2）x2﹣4x+1＝0有两个不相等的实数根，则k的取值范围是 ．
14．如图，点A，B为定点，P是l上一动点，点M，PB的中点，对下列各值：①线段MN的长；③△PMN的面积；④直线MN；⑤∠APB的大小．其中不会随点P的移动而改变的是 （填序号）
15．如图，在平行四边形ABCD中，AB＝6，∠B＝60°，∠BAD与∠CDA的角平分线AE、DF相交于点G，则图中阴影部分的面积是 ．
16．如图，在平面直角坐标系xOy中，平行四边形OABC的顶点A（12，0），（14，6），将平行四边形OABC绕点O逆时针方向旋转得到平行四边形OA′B′C′，当点C′落在BC的延长线上时，则线段C′E的长度为 ．
三．解答题（共8小题）
17．计算题
（1）（）2﹣+
（2）（）÷
18．解下列方程
（1）x2﹣2x＝0
（2）3x（x﹣1）＝2﹣2x
19．已知：如图，在四边形ABCD中，AB∥CD，E，且AE＝CF，DF∥BE．求证：四边形ABCD为平行四边形．
20．如图，在6×6的网格中，每个小正方形的边长为1（小正方形的顶点）上，试在各网格中画出顶点在格点上，面积为6
21．某校德育处积极开展“预防新冠病毒知识知多少”宣传活动，组织举办了一次防病毒知识竞赛，本次竞赛满分10分，成绩达到6分及6分以上为合格，达到9分或10分为优秀在这次竞赛中
解答下列问题：
（1）填空：a＝ ；b＝ ．
（2）小敏说：“这次竞赛我得了7分，在我们小组中排名属中游略偏上．”观察上面表格后思考判断，小敏属于 （填“甲”或“乙”）组的学生．
（3）甲组同学说他们组的合格率、优秀率均高于乙组，所以他们组的成绩比乙组好．但乙组同学不同意甲组同学的说法，认为他们的成绩要好于甲组请你写出两条支持乙组同学观点的理由．
22．有一种螃蟹，从海上捕获后不放养最多只能存活两天，如果放养在塘内，但每天也会有一定数量的螃蟹死去，假设放养期间内螃蟹的个体重量基本保护不变．现有一条经销商，此时市场价为30元/kg．据测算此后每千克的活螃蟹市场价每天可上升1元，但是，且平均每天还有10kg的蟹死去，假定死蟹均于当天全部售出
（1）设x天后每千克活蟹的市场价为P元，请写出P关于x的函数关系式；
（2）如果经销商将这批蟹出售后能获利6250元，那么他应放养多少天后再一次性售出？
23．如图，在△ABC中，∠ACB＝90°，BC长为半径画弧，交线段
AB于点D；以点A为圆心，AD长为半径画弧，连接CD．
（1）若∠A＝28°，求∠ACD的度数．
（2）设BC＝a，AC＝b．
①线段AD的长是方程x2+2ax﹣b2＝0的一个根吗？说明理由．
②若AD＝EC，求的值．
24．我们规定：有一组邻边相等，且这组邻边的夹角为60°的凸四边形叫做“准筝形”．
（1）如图1，在四边形ABCD中，∠A+∠C＝270°，AB＝CB，求证：四边形ABCD是“准筝形”；
（2）小军同学研究“准筝形”时，思索这样一道题：如图2，“准筝形”ABCD，∠BAD＝∠BCD＝60°，BC＝5，求AC的长．
小军研究后发现，可以CD为边向外作等边三角形，构造手拉手全等模型
（3）如图3，在△ABC中，∠A＝45°，设D是△ABC所在平面内一点，当四边形ABCD是“准筝形”时
组别
平均分
中位数
方差
合格率
优秀率
甲组
6.8
a
3.76
90%
30%
乙组
b
7.5
1.96
80%
20%