






中考冲刺-数学-第14课 二次函数及其图像
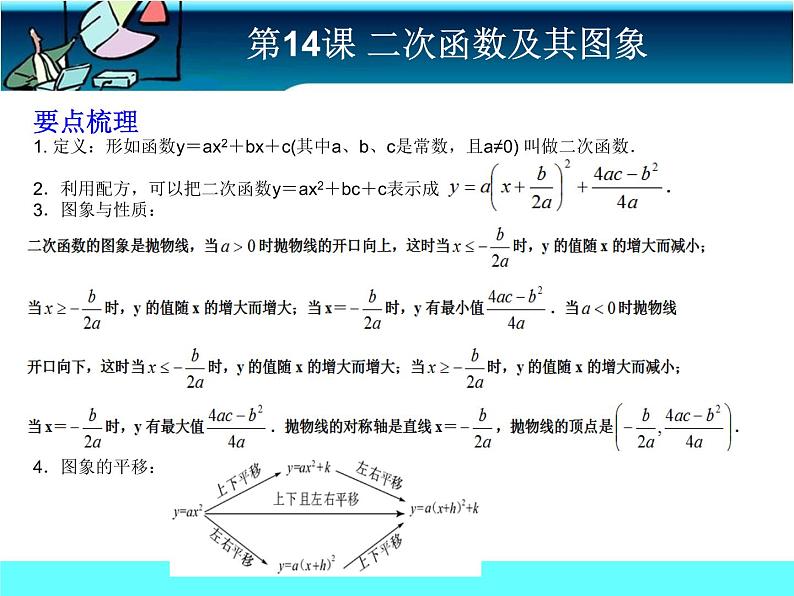
展开要点梳理1. 定义:形如函数y=ax2+bx+c(其中a、b、c是常数,且a≠0) 叫做二次函数.2.利用配方,可以把二次函数y=ax2+bc+c表示成3.图象与性质: 4.图象的平移:
第14课 二次函数及其图象
二次函数的三种解析式 (1)一般式y=ax2+bx+c(a,b,c是常数,a≠0); (2)交点式y=a(x-x1)(x-x2 )(a,x1,x2是常数,a≠0); (3)顶点式y=a(x+h)2+k(a,h,k是常数,a≠0).抛物线的顶点常见的三种变动方式 (1)开口反向(或旋转180°),此时顶点坐标不变,只是a的符号相反; (2)两抛物线关于x轴对称,此时顶点关于x轴对称,a的符号相反; (3)两抛物线关于y轴对称,此时顶点关于y轴对称,a的符号不变.二次函数与二次方程间的关系 已知二次函数y=ax2+bx+c的函数值为k,求自变量x的值,就是解一元二次方程ax2+bx+c=k;反过来,解一元二次方程ax2+bx+c=k,就是把二次函数y=ax2+bx+c-k的函数值看做0,求自变量x的值. 二次函数与二次不等式间的关系 “一元二次不等式”实际上是指二次函数的函数值“y>0,y<0 或y≥0,y≤0”, 从图像上看是指抛物线在x轴上方或x轴下方的情况.
考点巩固测试 1. 已知一抛物线与x轴的交点是A(-2,0)、B(1,0),且经过C(2,8). (1)求该抛物线的解析式; (2)求该抛物线的顶点坐标. 解 (1)设y=a(x+2)(x-1),又抛物线过C(2,8), ∴8=a(2+2)(2-1),a=2. ∴y=2(x+2)(x-1)=2(x2+x-2)=2x2+2x-4. 感悟提高 根据不同条件,选择不同设法. (1)若已知图象上的三个点,则设所求的二次函数为一般式y=ax2+bx+c(a≠0),将已知条件代入,列方程组,求出a、b、c的值; (2)若已知图象的顶点坐标或对称轴方程,函数最值,则设所求二次函数为顶点式y=a(x+m)2+k(a≠0),将已知条件代入,求出待定系数; (3)若已知抛物线与x轴的交点,则设抛物线的解析式为交点式y=a(x-x1)(x-x2)(a≠0),再将另一条件代入,可求出a值.
变式测试1 已知二次函数y=-x2+bx+c图象如图所示,它与x轴交点坐标为(-1,0),与y轴的交点坐标为(0,3). (1)求出b、c的值,并写出此二次函数的解析式; (2)根据图象,写出函数的值y为正数时,自变量x的取值范围.
解 (1)由题意,解得b=2, c=3∴y=-x2+2x+3.(2)令y=0,得-x2+2x+3=0,解得x1=-1,x2=3.故当y>0时,x的取值范围是-1
变式测试2 (2012·珠海) 如图,二次函数y=(x-2)2+m的图象与y轴交于点C,点B是点C关于该二次函数图象的对称轴对称的点.已知一次函数y=kx+b的图象经过该二次函数图象上点A(1,0)及点B. (1)求二次函数与一次函数的解析式; (2)根据图象,写出满足kx+b≥(x-2)2+m的x的取值范围. 解 (1)将点A(1,0)代入y=(x-2)2+m,得 (1-2)2+m=0,1+m=0,m=-1, 则二次函数解析式为y=(x-2)2-1. 当x=0时,y=4-1=3,故C点坐标为(0,3). 由于C和B关于对称轴对称,则设B点坐标为(x,3), 令y=3,有(x-2)2-1=3,解得x=4或x=0, 则B点坐标为(4,3). 设一次函数解析式为y=kx+b, 将A(1,0)、B(4,3)代入y=kx+b,得 解得则一次函数解析式为y=x-1.
3. (2013·嘉兴) 某汽车租赁公司拥有20辆汽车.据统计,当每辆车的日租金为400元时,可全部租出;当每辆车的日租金每增加50元,未租出的车将增加1辆;公司平均每日的各项支出共4800元.设公司每日租出x辆车时,日收益为y元.(日收益=日租金收入-平均每日各项支出) (1)公司每日租出x辆车时,每辆车的日租金为________元;(用含x的代数式表示) (2)当每日租出多少辆时,租赁公司日收益最大?最大是多少元? (3)当每日租出多少辆时,租赁公司的日收益不盈也不亏?解 (1)∵某汽车租赁公司拥有20辆汽车.据统计,当每辆车的日租金为400元时,可全部租出;当每辆车的日租金每增加50元,未租出的车将增加1辆;∴当全部未租出时,每辆租金为:400+20×50=1400元,∴公司每日租出x辆车时,每辆车的日租金为:1400-50x.(2)根据题意得出:y=x(-50x+1400)-4800=-50(x-14)2+5000.当x=14时,在范围内,y有最大值5000.∴当日租出14辆时,租赁公司日收益最大,最大值为5000元.(3)要使租赁公司日收益不盈也不亏,即y=0.即-50(x-14)2+5000=0,解得x1=24,x2=4,∵x=24不合题意,舍去,∴当日租出4辆时,租赁公司日收益不盈也不亏.
感悟提高 解决最值问题的关键是根据已知条件建立二次函数模型,利用二次函数的最大值或最小值来解.变式测试3 (2012·无锡) 如图,在边长为24 cm的正方形纸片ABCD上,剪去图中阴影部分的四个全等的等腰直角三角形,再沿图中的虚线折起,折成一个长方体形状的包装盒(A、B、C、D四个顶点正好重合于上底面上一点).已知E、F在AB边上,是被剪去的一个等腰直角三角形斜边的两个端点,设AE=BF=x(cm). (1)若折成的包装盒恰好是个正方体,试求这个包装盒的体积V; (2)某广告商要求包装盒的表面(不含下底面)面积S最大,试问x应取何值? 解 (1)根据题意,知这个正方体的底面边长(2)设包装盒的底面边长为a cm,高为h cm,=-6x2+96x=-6(x-8)2+384,∵0<x<12,∴当x=8时,S取得最大值384 cm2.
4. (2013·兰州) 如图,Rt△ABO的两直角边OA、OB分别在x轴的负半轴和y轴的正半轴上,O为坐标原点,A、B两点的坐标分别为(-3,0)、(0,4),抛物线y=(⅔)x2+bx+c经过点B,且顶点在直线x=5/2上. (1)求抛物线对应的函数关系式; (2)若把△ABO沿x轴向右平移得到△DCE,点A、B、O的对应点分别是D、C、E,当四边形ABCD是菱形时,试判断点C和点D是否在该抛物线上,并说明理由; 解 在Rt△ABO中,OA=3,OB=4,
∵四边形ABCD是菱形,∴BC=CD=DA=AB=5, ∴C、D两点的坐标分别是(5,4)、(2,0). ∴点C和点D都在所求抛物线上. (3)在(2)的条件下,连接BD,已知对称轴上存在一点P,使得△PBD的周长最小,求出P点的坐标;解 设CD与对称轴交于点P,则P为所求的点.设直线CD对应的函数关系式为y=kx+b,则 解得 (4)在(2)、(3)的条件下,若点M是线段OB上的一个动点(点M与点O、B不重合),过点M作MN∥BD交x轴于点N,连接PM、PN,设OM的长为t,△PMN的面积为S,求S和t的函数关系式,并写出自变量t的取值范围,S是否存在最大值?若存在,求出最大值和此时M点的坐标;若不存在,说明理由.
感悟提高 此题主要考查了二次函数的综合应用,以及菱形性质和待定系数法求解析式;求图形面积最值,利用二次函数的最值求出是解题关键.变式测试4 (2013·菏泽)如图,在平面直角坐标系中放置一直角三角板,其顶点为A(0,1),B(2,0),O(0,0),将此三角板绕原点O逆时针旋转90°,得到△A′B′O. (1)一抛物线经过点A′、B′、B,求该抛物线的解析式; (2)设点P是在第一象限内抛物线上的一动点,是否存在点P,使四边形PB′A′B的面积是△A′B′O面积的4倍?若存在,请求出点P的坐标;若不存在,请说明理由; (3)在(2)的条件下,试指出四边形PB′A′B是哪种形状的四边形?并写出四边形PB′A′B的两条性质.解 (1)∵△A′B′O是由△ABO绕原点O逆时针旋转90°得到的,又A(0,1),B(2,0),O(0,0),∴A′(-1,0),B′(0,2).设抛物线的解析式为y=ax2+bx+c(a≠0),∵抛物线经过点A′、B′、B,∴满足条件的抛物线的解析式为y=-x2+x+2.
(2)P为第一象限内抛物线上的一动点,设P(x,y),则x>0,y>0,P点坐标满足y=-x2+x+2.连接PB,PO,PB′,则S四边形PB′A′B =SΔB′OA′ +SΔPB′O +SΔPOB = ½×1×2+½×2×x+½×2×y=x+(-x2+x+2)+1=-x2+2x+3.假设四边形PB′A′B的面积是△A′B′O面积的4倍,则-x2+2x+3=4,即x2-2x+1=0,解得x=1,此时y=-12+1+2=2,即P(1,2).∴存在点P(1,2),使四边形PB′A′B的面积是△A′B′O面积的4倍. (3)四边形PB′A′B为等腰梯形,答案不唯一,下面性质中的任意2个均可.①等腰梯形同一底上的两个内角相等;②等腰梯形对角线相等;③等腰梯形上底与下底平行;④等腰梯形两腰相等. 或用符号表示:①∠B′A′B=∠PBA′或∠A′B′P=∠BPB′;②PA′=B′B; ③B′P∥A′B; ④B′A′=PB.
《中考大一轮数学复习》课件 课时16 二次函数及其图像: 这是一份《中考大一轮数学复习》课件 课时16 二次函数及其图像,共21页。PPT课件主要包含了夯实基本知已知彼,知识结构梳理,课前预测你很棒,热点看台快速提升,y=2x2+1,答案m=1或m=3等内容,欢迎下载使用。
《中考大一轮数学复习》课件 课时16 二次函数及其图像: 这是一份《中考大一轮数学复习》课件 课时16 二次函数及其图像,共21页。PPT课件主要包含了夯实基本知已知彼,知识结构梳理,课前预测你很棒,热点看台快速提升,y=2x2+1,答案m=1或m=3等内容,欢迎下载使用。
中考冲刺-数学-第31课图像的轴对称: 这是一份中考冲刺-数学-第31课图像的轴对称,共14页。PPT课件主要包含了考点跟踪训练等内容,欢迎下载使用。












