中考冲刺-数学-第35课用坐标表示图形变换

这是一份中考冲刺-数学-第35课用坐标表示图形变换，共14页。PPT课件主要包含了考点跟踪训练等内容，欢迎下载使用。

要点梳理　　1．平面直角坐标系：在平面内具有公共原点 而且互相垂直 的两条数轴，就构成了平面直角坐标系，简称坐标系．建立了直角坐标系的平面叫坐标平面，x轴与y轴把坐标平面分成四个部分，称为四个象限，按逆时针顺序依次叫第一象限、第二象限、第三象限、第四象限．
第35课　用坐标表示图形变换
各象限内和坐标轴上的点和坐标的规律：第一象限：(＋，＋)正正；第二象限：(－，＋)负正；第三象限：(－，－)负负；第四象限：(＋，－)正负；x轴正方向：(＋，0)；x轴负方向：(－，0); y轴正方向：(0，＋)；y轴负方向：(0，－)；x轴上的点的纵坐标为0；y轴上的点的横坐标为0；原点坐标为(0，0)．2．建立了坐标系的平面，有序实数对与坐标平面内的点一一对应．3．对称点坐标的规律：　　(1)坐标平面内，点P(x，y)关于x轴(横轴)的对称点P1的坐标为(x，－y) ；　　(2)坐标平面内，点P(x，y)关于y轴(纵轴)的对称点P2的坐标为(－x，y) ；　　(3)坐标平面内，点P(x，y)关于原点的对称点P3的坐标为(－x，－y) ．　　可用口诀记忆：关于谁轴对称谁不变，关于原点对称都要变．4．平移前后，点的坐标的变化规律：　　(1)点(x，y)左移a个单位长度：(x－a，y)；　　(2)点(x，y)右移a个单位长度：(x＋a，y)；　　(3)点(x，y)上移a个单位长度：(x，y＋a)；　　(4)点(x，y)下移a个单位长度：(x，y－a)．　　可用口诀记忆：正向右负向左，正向上负向下．
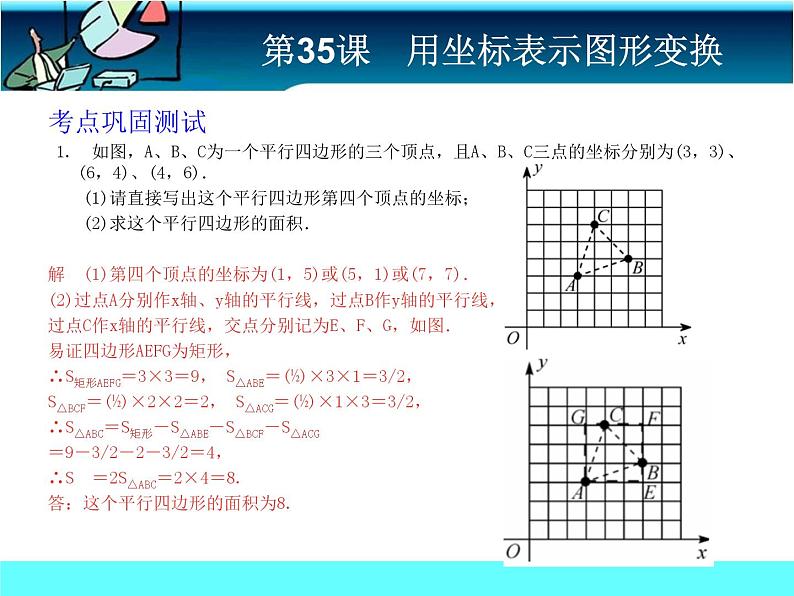
考点巩固测试 1.　如图，A、B、C为一个平行四边形的三个顶点，且A、B、C三点的坐标分别为(3，3)、(6，4)、(4，6)． (1)请直接写出这个平行四边形第四个顶点的坐标；　　(2)求这个平行四边形的面积． 解　(1)第四个顶点的坐标为(1，5)或(5，1)或(7，7)．(2)过点A分别作x轴、y轴的平行线，过点B作y轴的平行线，过点C作x轴的平行线，交点分别记为E、F、G，如图．易证四边形AEFG为矩形，∴S矩形AEFG＝3×3＝9， S△ABE＝(½)×3×1＝3/2，S△BCF＝(½)×2×2＝2， S△ACG＝(½)×1×3＝3/2，∴S△ABC＝S矩形－S△ABE－S△BCF－S△ACG＝9－3/2－2－3/2＝4，∴S＝2S△ABC＝2×4＝8.答：这个平行四边形的面积为8.
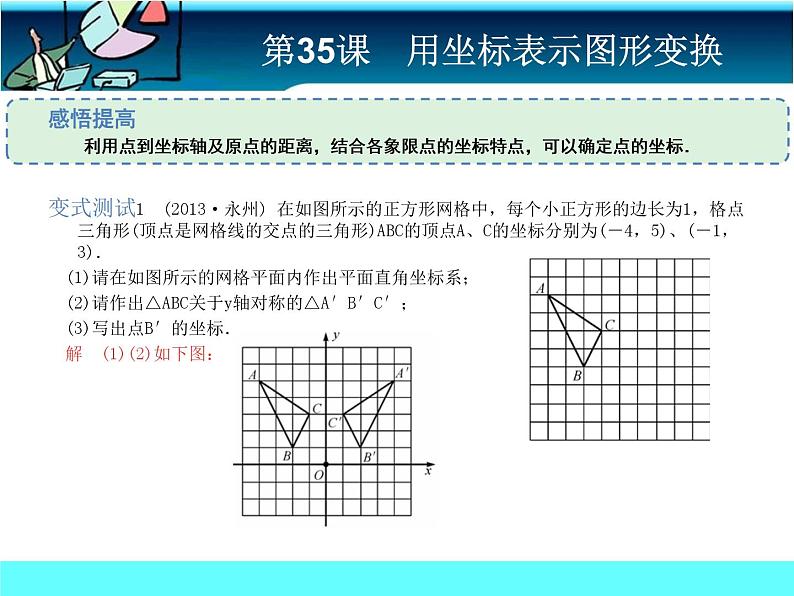
感悟提高　　利用点到坐标轴及原点的距离，结合各象限点的坐标特点，可以确定点的坐标．变式测试1　(2013·永州) 在如图所示的正方形网格中，每个小正方形的边长为1，格点三角形(顶点是网格线的交点的三角形)ABC的顶点A、C的坐标分别为(－4，5)、(－1，3)．　(1)请在如图所示的网格平面内作出平面直角坐标系；　(2)请作出△ABC关于y轴对称的△A′B′C′；　(3)写出点B′的坐标．　解　(1)(2)如下图：
2.　已知坐标平面上的机器人接受指令“[a，A]”(a≥0，0°变式测试2　(2011·黔东南) 在平面直角坐标系中，设点P到原点O的距离为ρ，OP与x轴正方向的夹角为α，则用[ρ，α] 表示点P的极坐标，显然，点P的极坐标与它的坐标存在一一对应关系．例如：点P的坐标为(1，1)，则其极坐标为 [ ，45°]．若点Q的极坐标为[4，60°]，则点Q的坐标为 (　　)　　　　解析　作QA⊥x轴于点A，　　则OQ＝4，∠QOA＝60°，　　∴OA＝OQ×cs 60°＝2，　　
3.　(2012·泰安) 如图，菱形OABC的顶点O在坐标原点，顶点A在x轴上，∠B＝120°，OA＝2，将菱形OABC绕原点顺时针旋转105°至OA′B′C′的位置，则点B′的坐标为 (　　)　　 解析　连接OB、OB′，过点B′作B′E⊥x轴于E，根据题意得：∠BOB′＝105°，∵四边形OABC是菱形，∴OA＝AB，∠AOB＝½∠AOC＝½∠ABC＝½×120°＝60°，∴△OAB是等边三角形，∴OB＝OA＝2，∴∠AOB′＝∠BOB′－∠AOB＝105°－60°＝45°，OB′＝OB＝2，
感悟提高 本题考察坐标与图形变化——旋转以及菱形的性质．变式测试3　(2012·南通) 线段MN在直角坐标系中的位置如图所示，线段M1N1与MN关于y轴对称，则点M的对应的点M1的坐标为 (　　)　　A．(4，2) 　　B．(－4，2)　　C．(－4，－2) 　　D．(4，－2) 解析　根据坐标系可得M点坐标是(－4，－2)，故点M关于y轴的对应点M′的坐标为(4，－2)．
4.问题背景：在△ABC中，AB、BC、AC三边的长分别为 求这个三角形的面积．小辉同学在解答这道题时，先建立一个正方形网格(每个小正方形的边长为1)，再在网格中画出格点△ABC(即△ABC三个顶点都在小正方形的顶点处)，如图①所示，这样不需求△ABC的高，而借用网格就能计算出它的面积．　　 (1)请你将△ABC的面积直接填写在横线上：________；(2)我们把上述求△ABC的面积的方法叫做构图法，若△ABC三边的长分别为 请利用图②的正方形网格(每个小正方形的边长为a)画出相应的△ABC，并求出它的面积； 　
　解 △ABC如图(2)所示(位置不唯一)．(3)△ABC三边的长分别为 试运用构图法求出这三角形的面积．解 构造△ABC如图(3)所示，＝12mn－2mn－3mn－2mn＝5mn.感悟提高 在平面直角坐标系或网格中求面积，有一定的规律，常以填空或选择题的形式出现，一般的做法是将难以求解的图形分割成易求解面积的图形，即构图法．
变式测试4　已知点A(－1，4)，B(2，2)，C(4，－1)，则△ABC的面积是________．解 如图：