中考冲刺-数学-第22课特殊三角形

这是一份中考冲刺-数学-第22课特殊三角形，共12页。PPT课件主要包含了第22课特殊三角形，考点跟踪训练等内容，欢迎下载使用。

要点梳理1．等腰三角形：　　(1)性质：两腰 相等，两底角 相等，底边上的高线、中线、顶角的角平分线“三线合一”；　　(2)判定：有两边相等、两角相等或两线合一的三角形是等腰三角形．2．等边三角形：　　　(1)性质：三边 相等，三内角都等于60° ；　　　(2)判定：三边相等、三内角相等或有一个角是60°的等腰三角形是等边三角形．3．直角三角形：在△ABC中，∠C＝90°.　　(1)性质：边与边的关系(勾股定理)：a2＋b2＝c2 ；　　(2)角与角的关系：∠A＋∠B＝90°；　　(3)边与角的关系： 若∠A＝30°，则a＝½c， b＝　　若a＝½c，则∠A＝30°；　　若∠A＝45°，则a＝b＝　　 若a＝ 则∠A＝45°；　　 斜边上的中线m＝½c＝R(其中R为三角形外接圆的半径)． (4)判定：有一个角是直角的三角形是直角三角形；如果三角形的三边长a、b、c满足a2＋b2＝c2，那么这个三角形是直角三角形；如果三角形一条边上的中线等于这条边的一半，那么这个三角形是直角三角形．
考点巩固测试 1.　(1)方程x2－9x＋18＝0的两个根是等腰三角形的底和腰，则这个三角形的周长为 (　　)　A．12 B．12或15 C．15 D．不能确定解析　解方程x2－9x＋18＝0，得x1＝3，x2＝6，周长为3＋6＋6＝15.(2)如果等腰三角形的一个内角是80°，那么顶角是________度．解析　顶角是80°，或当底角是80°时，顶角是180°－2×80°＝20°.感悟提高　　在等腰三角形中，如果没有明确底边和腰，某一边可以是底，也可以是腰．同样，某一角可以是底角也可以是顶角，必须仔细分类讨论．变式测试1　(1)(2011·株洲) 如图， △ABC中，AB＝AC，∠A＝36°，AC的垂直平分线交AB于E，D为垂足，连接EC.　　①求∠ECD的度数；　　②若CE＝5，求BC长．
解　①解法一：∵DE垂直平分AC，∴CE＝AE，∠ECD＝∠A＝36°. 解法二：∵DE垂直平分AC，∴AD＝CD，∠ADE＝∠CDE＝90°.又∵DE＝DE，∴△ADE≌△CDE，∠ECD＝∠A＝36°.②解法一：∵AB＝AC，∠A＝36°，　　　∴∠B＝∠ACB＝72°.　　　∵∠ECD＝∠A＝36°，　　　∴∠BCE＝∠ACB－∠ECD＝36°，　　　∴∠BEC＝180°－36°－72°＝72°＝∠B，　　　∴ BC＝EC＝5.解法二：∵AB＝AC，∠A＝36°，　　　∴∠B＝∠ACB＝72°， 　　　∴∠BEC＝∠A＋∠ECD＝72°， 　　　∴∠BEC＝∠B，∴BC＝EC＝5.(2)(2013·烟台) 等腰三角形的周长为14，其一边长为4，那么，它的底边为__．解析　①等腰三角形的底边为4；②等腰三角形的两腰为4时，则底边等于14－4－4＝6.
2.　如图，在等腰Rt△ABC中，∠BAC＝90°，点D是BC的中点，且AE＝BF，试判断△DEF的形状．　　　解　连接AD，在等腰Rt△ABC中，　　　∵AD是中线，　　　∴AD⊥BC，∠DAE＝½∠BAC＝45°，AD＝BD.　　　又∵∠B＝∠C＝45°，∴∠B＝∠DAE.　　　在△BDF和△ADE中，　　　∴△BDF≌△ADE(SAS)．∴DF＝DE，∠1＝∠2.　　　又∵∠3＋∠1＝90°，∴∠2＋∠3＝90°，　　　即∠EDF＝90°.∴△DEF也是等腰直角三角形．
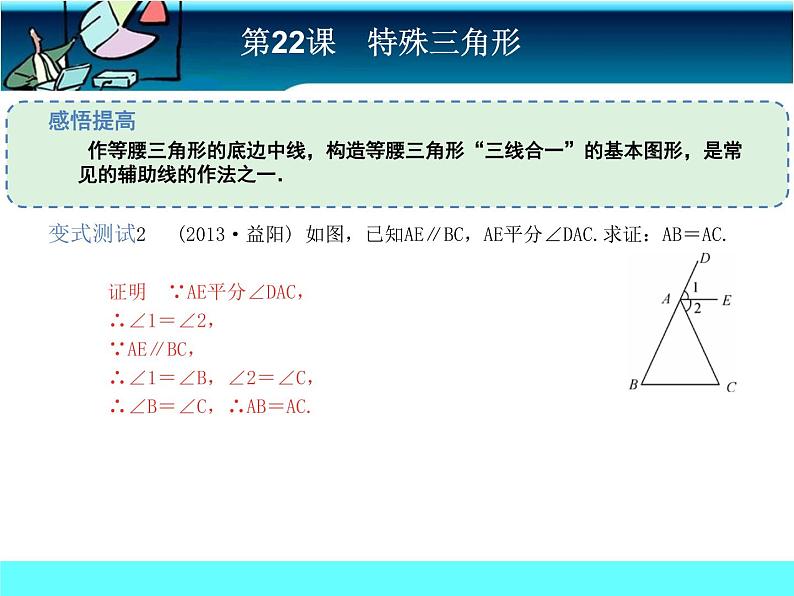
感悟提高　　作等腰三角形的底边中线，构造等腰三角形“三线合一”的基本图形，是常见的辅助线的作法之一．变式测试2　 (2013·益阳) 如图，已知AE∥BC，AE平分∠DAC.求证：AB＝AC.　　　证明　∵AE平分∠DAC，　　　∴∠1＝∠2，　　　∵AE∥BC，　　　∴∠1＝∠B，∠2＝∠C，　　　∴∠B＝∠C，∴AB＝AC.
3.　(2012·湘潭) 如图，△ABC是边长为3的等边三角形，将△ABC沿直线BC向右平移，使B点与C点重合，得到△DCE，连接BD，交AC于F.　　(1)猜想AC与BD的位置关系，并证明你的结论；　　(2)求线段BD的长．　　　解　(1)∵△DCE由△ABC平移而成，　　　∴BE＝2BC＝6，DE＝AC＝3，∠E＝∠DCE＝60°.　　　∵BC＝DC＝3，　　　∴∠CBD＝∠CDB.　　　又∵∠CBD＋∠CDB＝∠DCE＝60°，　　　∴∠CDB＝30°，∴∠BDE＝90°， 　　　∴BD⊥DE.　　　∵AC∥DE，∴AC⊥BD.　　　(2)在Rt△BED中，∵BE＝6，DE＝3，　　　
感悟提高　　在解题的过程中要充分利用等边三角形特有的性质，每个角都相等，每条边都相等，这可以让我们轻松找到证明全等所需的条件．变式测试3　如图，在等边△ABC中，点D、E分别在边BC、AB上，且BD＝AE，AD与CE交于点F.　(1)求证：AD＝CE；　　(2)求∠DFC的度数．　　　解　(1)在等边△ABC中，　　　AB＝AC，∠BAC＝∠CBA＝60°，　　　又∵BD＝AE，　　　∴△ABD≌△CAE，　　　∴AD＝CE.　　　(2)∵△ABD≌△CAE，∴∠BAD＝∠ECA.　　　∵∠DFC是△AFC的外角，　　　∴∠DFC＝∠ECA＋∠DAC＝∠BAD＋∠DAC＝∠BAC＝60°.
　　4.(1)如图，已知△ABC中，∠ABC＝90°，AB＝BC，三角形的顶点在相互平行的三条直线l1、l2、l3上，且l1、l2之间的距离为2，l2、l3之间的距离为3，则AC的长是 (　　)　　解析　分别过A、C画AD⊥l3，CE⊥l3，垂足分别为D、E，易证明△ABD≌△BCE，∴AD＝BE＝3，BD＝CE＝3＋2＝5. 在Rt△ABD中，在Rt△ABC中，AB＝BC，(2)如图，在钝角三角形ABC中，BC＝9，AB＝17，AC＝10，AD⊥BC，交BC的延长线于D，求AD的长．　　　解　在Rt△ABD中，设CD＝x，　　　则AD2＝AB2－BD2＝172－(9＋x)2，　　　在Rt△ACD中，AD2＝AC2－CD2＝102－x2，　　　∴172－(9＋x)2＝102－x2，　解得x＝6，　　　∴在Rt△ACD中，
感悟提高　　在线段的长无法直接求出时，可利用另一线段把这一线段表示出来，然后利用勾股定理得到一个方程，最后得解，这是利用勾股定理解决线段长的常用方法．变式测试4　(2012·宁波)勾股定理是几何中的一个重要定理．在我国古算书《周髀算经》中就有“若勾三， 股四，则弦五”的记载．如图1是由边长相等的小正方形和直角三角形构成的，可以用其面积关系验证勾股定理．图2是由图1放入矩形内得到的，∠BAC＝90°，AB＝3，AC＝4，则D、E、F、G、H、I都在矩形KLMJ的边上，则矩形KLMJ的面积为 (　　)　　A．90 B．100 C．110 D．121解析　如图，延长AB交KF于点O，延长AC交GM于点P，所以，四边形AOLP是正方形，边长AO＝AB＋AC＝3＋4＝7，所以，KL＝3＋7＝10，LM＝4＋7＝11，因此，矩形KLMJ的面积为10×11＝110.