




勾股定理的逆定理
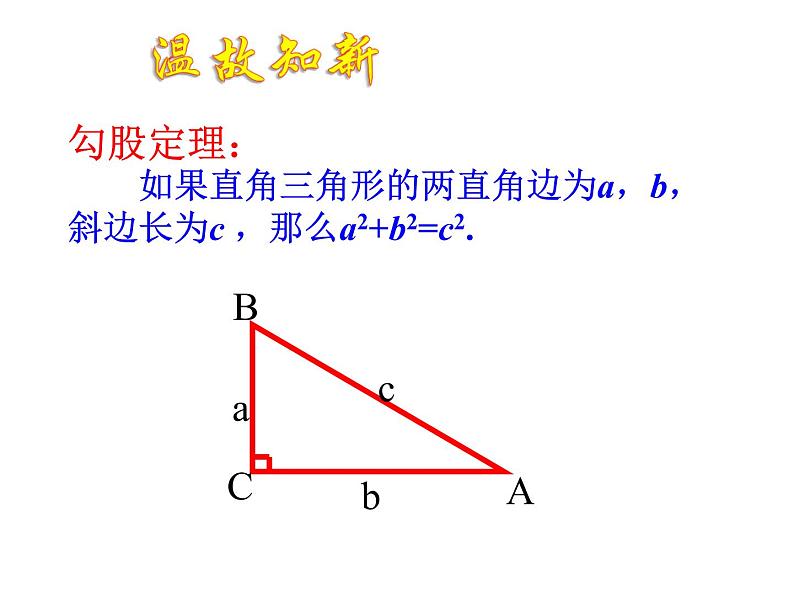
展开勾股定理: 如果直角三角形的两直角边为a,b,斜边长为c ,那么a2+b2=c2.
小明想要检测雕塑底座正面的 AD 边和BC边是否分别垂直于底边AB,但他随身只带了卷尺.
你能帮助小明解决这个问题吗?
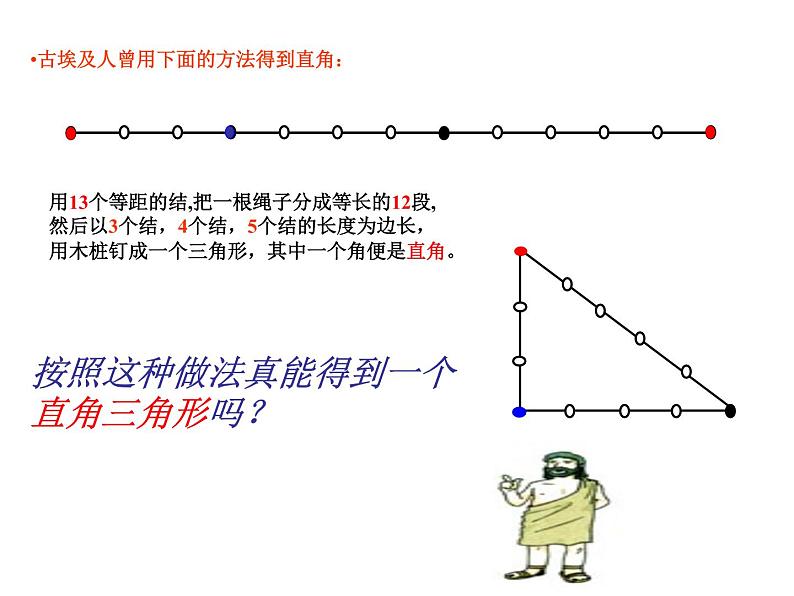
按照这种做法真能得到一个直角三角形吗?
古埃及人曾用下面的方法得到直角:
用13个等距的结,把一根绳子分成等长的12段,然后以3个结,4个结,5个结的长度为边长,用木桩钉成一个三角形,其中一个角便是直角。
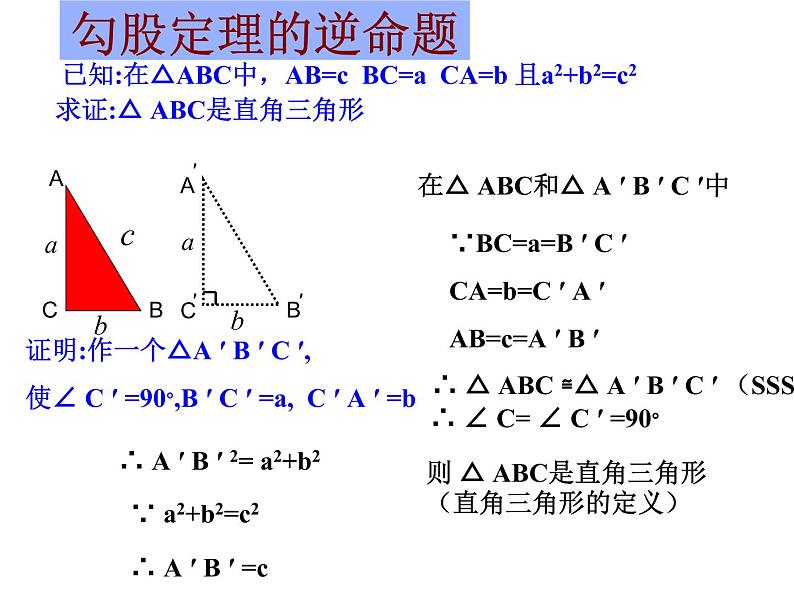
∴ A ′ B ′ 2= a2+b2
∴ A ′ B ′ =c
∴ △ ABC ≌△ A ′ B ′ C ′ (SSS)
∴ ∠ C= ∠ C ′ =90°
∵BC=a=B ′ C ′CA=b=C ′ A ′AB=c=A ′ B ′
已知:在△ABC中,AB=c BC=a CA=b 且a2+b2=c2
求证:△ ABC是直角三角形
证明:作一个△A ′ B ′ C ′,使∠ C ′ =90°,B ′ C ′ =a, C ′ A ′ =b
在△ ABC和△ A ′ B ′ C ′中
则 △ ABC是直角三角形(直角三角形的定义)
例1 判断由a、b、c组成的三角形是不是直角三角形:(1) a=15 , b =8 , c=17
(2) a=13 , b =15 , c=14
分析:由勾股定理的逆定理,判断三角形是不是直角三角形,只要看两条较小边的平方和是否等于最大边的平方。
解:∵152+82=225+64=289 172=289 ∴ 152+82=172 ∴这个三角形是直角三角形
判断由线段a、b、c组成的三角形是不是直角三角形:(1)a=5,b=13,c=12;(2)a=m2-n2,b=m2+n2,c=2mn(m>n,m、n是正整数)
解;(1)∵a2 = 25,b2 = 169, c2 = 144∴ a2 + c2 = b2即: 三角形是直角三角形
(2)∵a2 = (m2 - n2 )2 = m4 - 2m2n2 + n4, b2 = (m2 + n2 )2 = m4 + 2m2n2 + n4, c2 = (2mn )2 = 4m2n2又∵m4 - 2m2n2 + n4 + 4m2n2 = m4 + 2m2n2 + n4 ∴ a2 + c2 = b2即: 三角形是直角三角形
下面以a,b,c为边长的三角形是不是直角三角形?如果是那么哪一个角是直角?
(1) a=25 b=20 c=15 ____ _____ ;
(2) a=13 b=14 c=15 ____ _____ ;
(4) a:b: c=3:4:5 _____ _____ ;
像3,4,5,能够成为直角三角形三条边长的三个正整数,称为勾股数.
例1: “远航”号、“海天”号轮船同时离开港口,各自沿一固定方向航行,“远航”号每小时航行16海里,“海天”号每小时航行12海里。它们离开港口一个半小时后相距30海里。如果知道“远航”号沿东北方向航行,能知道“海天”号沿哪个方向航行吗?
例2:如图,有一块地,已知,AD=4m,CD=3m,∠ADC=90°,AB=13m,BC=12m。求这块地的面积。
如图,是一块四边形绿地示意图,其中AB长24米,BC长20米,CD长15米,DA长7米,∠ C=90度求:绿地ABCD的面积。
互逆命题: 两个命题中, 如果第一个命题的题设是第二个命题的结论, 而第一个命题的结论又是第二个命题的题设,那么这两个命题叫做互逆命题. 如果把其中一个叫做原命题, 那么另一个叫做它的逆命题. 互逆定理: 如果一个定理的逆命题经过证明是真命题, 那么它也是一个定理, 这两个定理叫做互逆定理, 其中一个叫做另一个的逆定理.
我们已经学习了一些互逆的定理,如:勾股定理及其逆定理,两直线平行,内错角相等;内错角相等,两直线平行.
想一想:互逆命题与互逆定理有何关系?
(1)两条直线平行,内错角相等.(2)如果两个实数相等,那么它们的平方相等.(3)如果两个实数相等,那么它们的绝对值相等.(4)全等三角形的对应角相等.
说出下列命题的逆命题.这些命题的逆命题成立吗?
逆命题: 内错角相等,两条直线平行. 成立
逆命题:如果两个实数的平方相等,那么这两个实数相等. 不成立
逆命题:如果两个实数的绝对值相等,那么这两个实数相等. 不成立
逆命题:对应角相等的两个三角形是全等三角形. 不成立
感悟: 原命题成立时, 逆命题有时成立, 有时不成立
一个命题是真命题,它逆命题却不一定是真命题.
随堂练习:1、将下列长度的三木棒首尾顺次连接,能组成直角三角形的是( )(A)1, 2, 3 (B)4, 6, 8 (C)5, 5, 4 (D)15,12, 9
2、如果线段a、b、c能组成直角三角形, 则它们的比可能是( ) (A)3:4:7; (B)5:12:13; (C)1:2:4; (D)1:3:5.
三角形的三边分别是a、b、c, 且满足(a+b)2-c2=2ab, 则此三角形是:( )A. 直角三角形; B. 是锐角三角形;是钝角三角形; D. 是等腰直角三角形.
4、一个零件的形状如下图所示,按规定这个零件中∠A和∠DBC都应为直角.工人师傅量出了这个零件各边尺寸,那么这个零件符合要求吗?
此时四边形ABCD的面积是多少?
5、 已知a、b、c为△ABC的三边,且 满足 a2+b2+c2+338=10a+24b+26c. 试判断△ABC的形状.
6、△ABC三边a,b,c为边向外作正方形,正三角形,以三边为直径作半圆,若S1+S2=S3成立,则
9.已知a.b.c为△ABC的三边,且满足 a2c2 – b2c2=a4 – b4,试判断△ABC的形状.解 ∵ a2c2- b2c2 = a4 – b4 (1) ∴ c2(a2 – b2) = (a2+ b2) (a2- b2) (2) ∴ c2 = a2 + b2 (3) ∴ △ABC是直角三角形问: (1) 上述解题过程,从哪一步开始出现错误?请写出该步的代号___(2) 错误原因是_________(3) 本题正确的结论是________
直角三角形或等腰三角形
10、如图:在Δ ABC中,AB=13㎝,BC=10㎝,BC边上的中线AD=12㎝,求证:AB=AC。
证明:∵AD是BC边上的中线, ∴BD=CD=1/2BC=5㎝ ∵在△ABD中,AB=13,BD=5,AD=12 ∴ BD2+AD2=52+122=169=AB2 ∴ △ABD是直角三角形。 ∴ △ACD也是直角三角形。 根据勾股定理得到:
初中数学人教版八年级下册17.2 勾股定理的逆定理教课内容ppt课件: 这是一份初中数学人教版八年级下册<a href="/sx/tb_c10262_t3/?tag_id=26" target="_blank">17.2 勾股定理的逆定理教课内容ppt课件</a>,共59页。PPT课件主要包含了我们大家来试试,勾股定理的逆命题,思考题等内容,欢迎下载使用。
人教版八年级下册17.2 勾股定理的逆定理授课课件ppt: 这是一份人教版八年级下册17.2 勾股定理的逆定理授课课件ppt,文件包含SectionBpptx、SectionA-1ppt、SectionA-2pptx、SelfCheckppt、SectionA1bmp3、SectionA2amp3、SectionA2bmp3、SectionA2dmp3、SectionB1cmp3、SectionB1dmp3、SectionB2bmp3、wordsandexpressionsUnit2mp3等12份课件配套教学资源,其中PPT共143页, 欢迎下载使用。
初中数学沪科版八年级下册18.2 勾股定理的逆定理教学课件ppt: 这是一份初中数学沪科版八年级下册18.2 勾股定理的逆定理教学课件ppt,共25页。PPT课件主要包含了知识要点,勾股定理的逆定理,勾股数,直角三角形,钝角三角形,即A′B′c,特别说明,c2625,c2121,练一练等内容,欢迎下载使用。












