


数学选修2-31.2排列与组合课文配套ppt课件
展开1.理解组合与组合数的概念.2.会推导组合数公式,并会应用公式求值.3.了解组合数的两个性质,并会求值、化简和证明.
①从全班50人中选出7人组成班委会;②从全班50人中选出7人分别担任班委中的7个不同的职务;③从1,2,5,11,19这五个数中取出两个数可得多少个不同的真分数;④从1,2,5,11,19这五个数中取出两个数可得多少个不同的差.(1)上面问题中是排列问题的是________.(2)①③的共同特征是什么?
[提示] (1)①与顺序无关不是排列问题,②④选取元素不同且与顺序有关是排列问题.③中任取出的两个数是不等的,只能确定唯一一个真分数,与顺序无关,不是排列问题.(2)取出的元素不同且无需排序
一般地,从n个________元素中_____________________ ____________________,叫做从n个不同元素中取出m个元素的一个组合.
取出m(m≤n)个元素
组合概念的理解(1)组合的定义中包含两个基本内容:一是“提取元素”;二是“合成一组”,因此,组合要完成“一件事件”是“取出m个元素后再不管顺序地并成一组”.(2)同排列的要求一样,组合也要求n个元素是不同的,被取出的m个元素也互不相同.(3)只要两个组合中的元素完全相同,则无论元素的顺序如何,都是相同的组合.只有当两个组合中的元素不完全相同时,才是不同的组合.
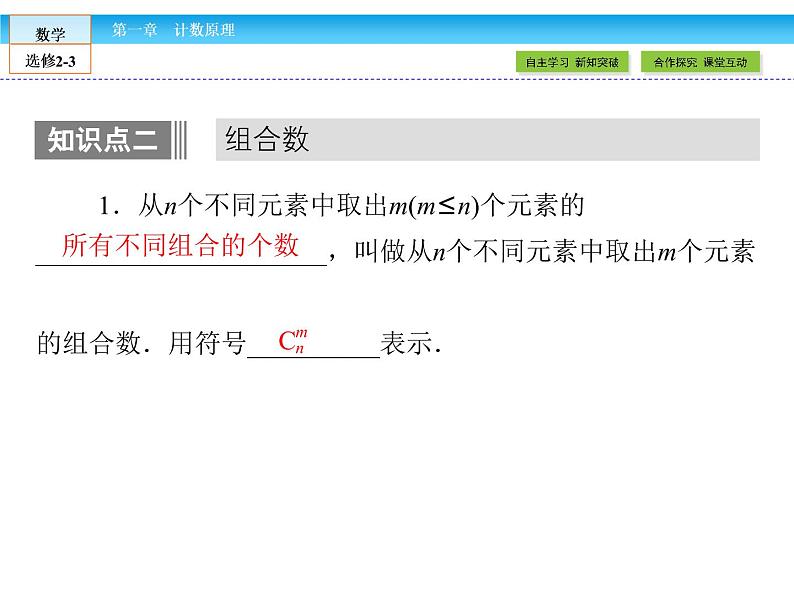
1.从n个不同元素中取出m(m≤n)个元素的______________________,叫做从n个不同元素中取出m个元素的组合数.用符号__________表示.
1.下面几个问题中属于组合问题的是( )①由1,2,3,4构成的双元素集合;②5个队进行单循环足球比赛的分组情况;③由1,2,3构成两位数的方法;④由1,2,3组成无重复数字的两位数的方法.A.①③ B.②④C.①②D.①②④解析: ①②取出元素与顺序无关,③④取出元素与顺序有关.答案: C
解析: 当x=3x-8时,解得x=4;当28-x=3x-8时,解得x=9.答案: A
3.按ABO血型系统学说,每个人的血型为A,B,O,AB四种之一,依血型遗传学,当且仅当父母中至少有一人的血型是AB型时,子女一定不是O型,若某人的血型为O型,则父母血型所有可能情况有________种.
4.判断下列各事件是排列问题,还是组合问题.(1)10个人相互各写一封信,共写多少封信?(2)10个人相互通一次电话,共通了多少次电话?(3)10支球队进行比赛,这次比赛冠、亚军获得者有多少种可能?(4)从10个人中选3个代表去开会,有多少种选法?(5)从10个人里选出3个不同学科的代表,有多少种选法?
解析: (1)是排列问题.因为发信人与收信人是有区别的.(2)是组合问题.因为甲与乙通了一次电话,也就是乙与甲通了一次电话,没有顺序的区别.(3)是排列问题.因为甲队得冠军、乙队得亚军与甲队得亚军、乙队得冠军是不一样的,是有顺序区别的.(4)是组合问题.因为3个代表之间没有顺序的区别.(5)是排列问题.因为3个人中,担任哪一科的代表是有顺序区别的.
判断下列问题是组合问题还是排列问题:(1)10人聚会,见面后每两人之间要握手相互问候,共需握手多少次?(2)10名同学分成人数相同的两个学习小组,共有多少种分法?
(3)从1,2,3,…,9九个数字中任取3个,然后把这三个数字相加得到一个和,这样的和共有多少个?(4)从a,b,c,d四名学生中选2名,去完成同一件工作,有多少种不同的选法? [思路点拨] 要分清是组合还是排列问题,只要确定取出的这些元素是否与顺序有关.
(1)两人之间相互握手,与顺序无关,故是组合问题;(2)分成的两个学习小组没有顺序,是组合问题;(3)取出3个数字之后,无论怎样改变这三个数字之间的顺序,其和均不变,此问题只与取出元素有关,而与元素的安排顺序无关,是组合问题;(4)2名学生完成的是同一件工作,没有顺序,是组合问题.
[规律方法] 区分排列与组合的办法是首先弄清楚事件是什么,区分的标志是有无顺序,而区分有无顺序的方法是:把问题的一个选择结果写出来,然后交换这个结果中任意两个元素的位置,看是否会产生新的变化,若有新变化,即说明有顺序,是排列问题;若无新变化,即说明无顺序,是组合问题.
1.判断下列问题是组合问题还是排列问题.并用组合数或排列数表示出来.(1)8人相互发一个电子邮件,共写了多少个邮件?(2)10支球队以单循环制进行比赛,共需要进行多少场比赛?(3)10支球队主客场制进行比赛,共需要进行多少场比赛?(4)有4张电影票,要在7人中确定4人去观看,不同的选法种数是多少?
(1)已知a,b,c,d这4个元素,写出每次取出2个元素的所有组合;(2)已知A,B,C,D,E这5个元素,写出每次取出3个元素的所有组合. [思路点拨] 先将元素按一定顺序写出,然后按照顺序用图示的方法逐步写出各个组合即可.
[规律方法] 1.此类列举所有从n个不同元素中选出m个元素的组合,可借助本例所示的“顺序后移法”(如方法一)或“树形图法”(如方法二),直观地写出组合做到不重复不遗漏.2.由于组合与顺序无关.故利用“顺序后移法”时箭头向后逐步推进,且写出的一个组合不可交换位置.如写出ab后,不必再交换位置为ba,因为它们是同一组合.画“树形图”时,应注意顶层及下枝的排列思路.防止重复或遗漏.
2.从5个不同元素a,b,c,d,e中取出2个,共有多少种不同的组合?
答案: (1)66 (2)466
人教版新课标B选修2-31.2.2组合教案配套课件ppt: 这是一份人教版新课标B选修2-31.2.2组合教案配套课件ppt,共17页。PPT课件主要包含了引例3,引例总结,组合定义,想一想,组合数,组合数公式等内容,欢迎下载使用。
人教版新课标B选修2-31.2.2组合图片课件ppt: 这是一份人教版新课标B选修2-31.2.2组合图片课件ppt,共17页。PPT课件主要包含了引例3,引例总结,组合定义,想一想,组合数,组合数公式等内容,欢迎下载使用。
高中数学人教版新课标A选修2-3第一章 计数原理综合与测试课文配套ppt课件: 这是一份高中数学人教版新课标A选修2-3第一章 计数原理综合与测试课文配套ppt课件,共25页。PPT课件主要包含了先看下面的问题,课前导入,新知探究,知识要点,例题1,例题2,∴原不等式可化为,例题3,例题4,性质1等内容,欢迎下载使用。













