广西壮族自治区南宁市宾阳县2020-2021学年七年级上学期期末数学试题（word版 含答案）

这是一份广西壮族自治区南宁市宾阳县2020-2021学年七年级上学期期末数学试题（word版 含答案），共20页。试卷主要包含了单选题，填空题，解答题等内容，欢迎下载使用。


一、单选题
1．3的相反数是（ ）
A．3B．-3C．D．
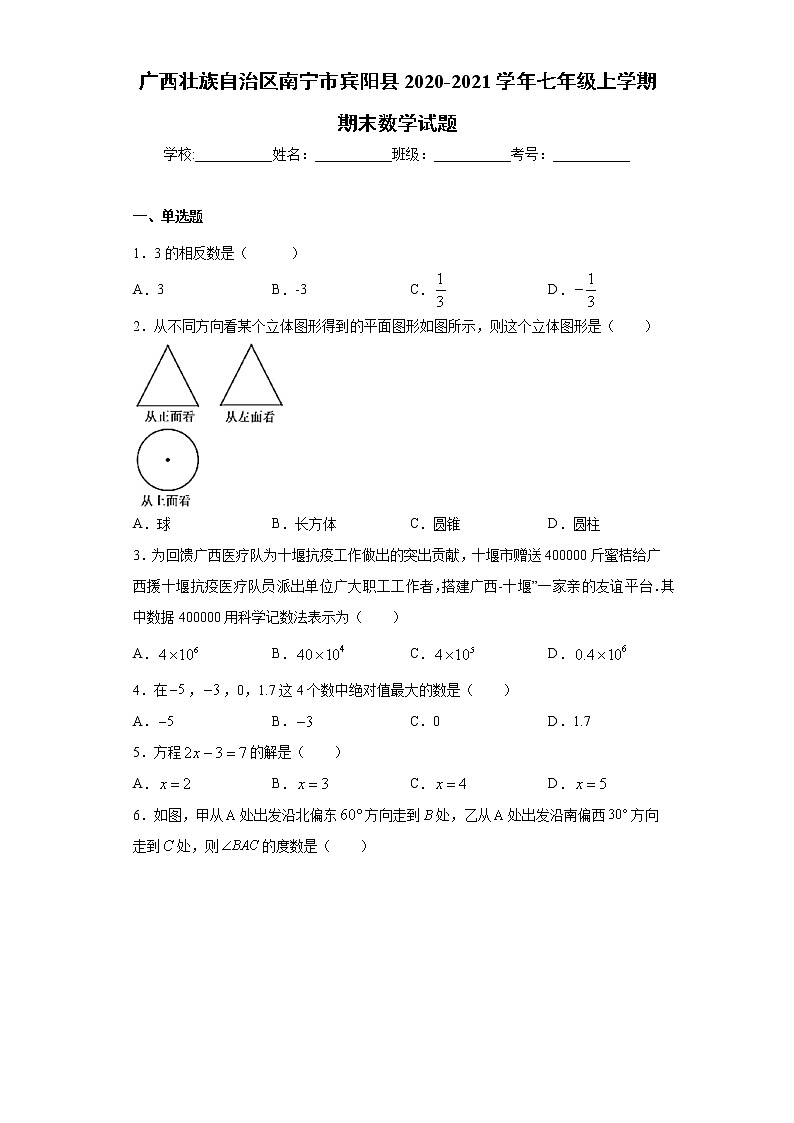
2．从不同方向看某个立体图形得到的平面图形如图所示，则这个立体图形是（ ）
A．球B．长方体C．圆锥D．圆柱
3．为回馈广西医疗队为十堰抗疫工作做出的突出贡献，十堰市赠送400000斤蜜桔给广西援十堰抗疫医疗队员派出单位广大职工工作者，搭建“广西-十堰”一家亲的友谊平台．其中数据400000用科学记数法表示为（ ）
A．B．C．D．
4．在，，0，1.7这4个数中绝对值最大的数是（ ）
A．B．C．0D．1.7
5．方程的解是（ ）
A．B．C．D．
6．如图，甲从处出发沿北偏东方向走到处，乙从处出发沿南偏西方向走到处，则的度数是（ ）
A．B．C．D．
7．在下列式子中变形正确的是（ ）
A．如果，那么B．如果，那么
C．如果，那么D．如果，那么
8．已知单项式的次数是3，则的值是（ ）
A．3B．4C．5D．6
9．有理数，在数轴上对应的点的位置如图所示，则下列结论正确的是（ ）
A．B．C．D．
10．已知线段，点是直线上一点，，若是的中点，是的中点，则线段的长度是（ ）
A．B．C．或D．或
11．一条地下管线由甲工程队单独铺设需要12天，由乙工程队单独铺设需要24天．如果由这两个工程队从两端同时施工，铺好这条管线需要的天数是（ ）
A．8天B．7天C．6天D．5天
12．（阅读理解）计算：，，，，观察算式，我们发现两位数乘11的速算方法：头尾一拉，中间相加，满十进一．
（拓展应用）已知一个两位数，十位上的数字是，个位上的数字是，这个两位数乘11，计算结果中十位上的数字可表示为（ ）
A．或B．或C．D．或
二、填空题
13．的余角是________°．
14．用四舍五入法对3.14取近似数精确到个位的结果是________．
15．一台无人机从高度为的位置开始，先上升，后下降，此时这台无人机所在的高度是________．
16．某电视台组织知识竞赛，共设20道选择题，各题分值相同，每题必答，下表记录了其中3名参赛者的得分情况，若参赛者得88分，则他答对________题．
17．把一副三角尺按如图所示拼在一起，其中，，三点在同一直线上，平分，平分，则________．
18．现有一张边长为1的正方形纸片，第一次沿着线段剪开，留下三角形；第二次取的中点，再沿着剪开，留下三角形；第三次取的中点，再沿着剪开，留下三角形；…，如此进行下去，在第次后，被剪去图形的面积之和是________．
三、解答题
19．计算：
（1）
（2）
20．解方程：
（）．
（）．
21．先化简，再求值：，其中，．
22．如图，已知直线和直线外三点，，，按下列要求画图：
（1）画射线；
（2）连接，延长至点，使得；
（3）在直线上确定点，使得点到点，点的距离之和最短．
23．近年来，我市香蕉产业不断做大做强，打造出“洛洛香”、“甜弯弯”等优质品业牌．如今又到了香蕉上市的季节，某商家以每箱60元的进价购入200箱香蕉，然后分批全部卖出．售价以每箱75元为标准，超过的部分记为正，低于的部分记为负，记录如下：
（1）求每箱香蕉的平均售价是多少元？
（2）该商家卖完所有香蕉所获利润为多少元？
24．2020年第17届东博会以“建‘一带一路’，共兴数字经济”为主题，在南宁国际会展中心同步举办实体展和云上东博会．为配合云直播，某展商需搭建一个长方形的直播舞台，已知长方形的长是米，宽比长小米．
（1）求长方形的周长（用含有，的式子表示）；
（2）当，满足条件：时，求长方形的周长．
25．如图，已知，是内的一条射线，且．
（1）求，的度数；
（2）作射线平分，在内作射线，使得，求的度数；
（3）过点作射线，若，求的度数．
26．甲地某果蔬批发市场计划运输一批蔬菜至乙地出售，为保证果蔬新鲜需用带冷柜的货车运输．现有，两种型号的冷柜车，若A型车的平均速度为50千米/小时，型车的平均速度为60千米/小时，从甲地到乙地型车比型车少用2小时．
（1）请求出型车从甲地到乙地的时间；
（2）已知型车每辆可运8吨，型车每辆可运7吨，若单独租用型车，则恰好装完；若单独租用相同数量的型车，则还剩3吨蔬菜没有装上车．问这批蔬菜共有多少吨？
（3）在（2）的条件下，冷柜车运完蔬菜从乙地返回时还需从乙地运输20吨水果（需用冷柜保鲜）回甲地，往返运输的相关数据如下表所示：
（参考公式：冷柜使用费=冷柜使用单价×使用时间车辆数目：总费用=路费+冷柜使用费）
请问应该单独安排型车还是型车运输才能使得本次往返甲乙两地的总费用较少？较少的总费用是多少？
参赛者
答对题目
答错题数
得分
19
1
94
20
0
100
10
10
40
超出标准（单位：元）
0
卖出数量（单位：箱）
50
20
40
30
30
30
路费单价
冷柜使用单价
1.5元/（千米辆）
型冷柜车
型冷柜车
10元/（小时辆）
8元/（小时辆）
参考答案
1．B
【分析】
根据相反数的定义进行解答即可．
【详解】
解：3的相反数是-3，
故选B．
【点睛】
本题考查的是相反数的定义，即只有符号不同的两个数叫做互为相反数．
2．C
【分析】
主视图、左视图、俯视图分别是从物体正面、左面和上面看，即可确定的图形．
【详解】
解：这个立体图形从上面看是一个圆，从正面和左面看是等腰三角形，所以这个立体图形是圆锥．
故选：C
【点睛】
本题考查了三视图的有关知识，具备一定的空间想象能力是解答关键．
3．C
【分析】
按科学记数法的要求，直接把数据表示为（其中，为整数）的形式即可．
【详解】
解：．
故选：C．
【点睛】
本题考查了用科学记数法表示绝对值大于1的数．掌握用科学记数法表示绝对值大于1的方法是解决本题的关键．科学记数法的表示形式为的形式，其中，为整数，表示时关键要正确确定的值以及的值．
4．A
【分析】
计算绝对值要根据绝对值的定义分别求出这四个数的绝对值，再进行比较即可.
【详解】
解：|- 5|=5， |- 3|=3， |0|=0，|1.7|=1.7，
∵5>3>1.7>0，
∴绝对值最大的数为-5，
故选: A.
【点睛】
本题考查的是绝对值的规律，一个 正数的绝对值是它本身，一个负数的绝对值是它的相反数， 0的绝对值是0.
5．D
【分析】
根据等式的性质移项、合并同类项得出2x=10，方程的两边都除以2即可求出答案.
【详解】
2x-3=7，
移项得: 2x= 10，
方程的两边都除以2得： x = 5，
故选D.
【点睛】
本题考查了对解一元一次方程和等式的性质等知识点的理解和掌握，关键是考查学生能否根据等式的性质正确解一元一次方程.
6．C
【分析】
根据题意得到∠EAD=∠DOF=90°，先求出∠BAD=30°，再根据∠BAC=∠EAD+∠DAF+∠CAF即可求解．
【详解】
解：如图，由题意得∠EAD=∠DOF=90°，
∵∠EAB=60°，
∴∠BAD=∠EAD-∠EAB=90°-60°=30°，
∴∠BAC=∠BAD+∠DAF+∠CAF=30°+90°+30°=120°．
故选：C
【点睛】
本题考查了角的和差的计算，理解方位角中东西方向和南北方向的夹角是90度时解题关键．
7．B
【分析】
根据等式的性质逐个判断即可．
【详解】
A、∵a=b，∴a+c=b+c，不是b-c，故本选项不符合题意；
B、∵a=b，∴两边都除以3得：，故本选项符合题意；
C、∵，∴两边都乘以3得：a=18，故本选项不符合题意；
D、∵a-b+c=0，∴两边都加b-c得：a=b-c，故本选项不符合题意，
故选B．
【点睛】
本题考查了等式的性质，能熟记等式的性质的内容是解此题的关键．
8．A
【分析】
根据单项式的次数定义即可得，则得解．
【详解】
解：根据单项式次数的定义得：
可得
故选A．
【点睛】
本题考查单项式的次数定义；关键在于知道单项式的次数等于各个字母的指数和．
9．C
【分析】
根据数轴即可判断a和b的符号以及绝对值的大小，根据有理数的加法法则即可判断．
【详解】
解：根据数轴可得且，且
由此可得，故A选项错误；
，故B选项错误；
，故C选项正确；
，故D选项错误．
故选C．
【点睛】
本题考查了利用数轴表示数，以及有理数的加法法则，根据数轴确定a和b的符号以及绝对值的大小是关键．
10．D
【分析】
根据线段中点的定义求出BM、BN，再分点C在线段AB的延长线上和点C在线段AB上两种情况讨论求解．
【详解】
解：∵M是AB的中点，N是BC的中点，
∴BM=AB=×10=5cm，
BN=BC=×4=2cm，
如图1，
当点C在线段AB的延长线上时，MN=BM+BN=5+2=7cm；
如图2，
当点C在线段AB上时，MN=BM-BN=5-2=3cm，
综上所述，线段MN的长度是7cm或3cm．
故选：D．
【点睛】
本题考查了两点间的距离，主要利用了线段中点的定义，难点在于要分情况讨论．
11．A
【分析】
设铺好这条管线需要x天，根据“甲乙工程队工作量之和=1”列方程，解方程即可求解．
【详解】
解：设铺好这条管线需要x天，列方程得
，
解得 x=8 ，
答：铺好这条管线需要8天．
故选：A
【点睛】
本题考查一元一次方程的应用，根据题意设出未知数，列出方程是解题关键．
12．D
【分析】
根据题目中的速算法可以解答本题.
【详解】
由题意可得，某一个两位数十位数字是a，个位数字是b，将这个两位数乘11，得到一个三位数，
则根据上述的方法可得：
当a+b< 10时，该三位数百位数字是a，十位数字是a + b，个位数字是b，
当a+b≥10时，结果的百位数字是a + 1，十位数字是a+b- 10，个位数字是b.
所以计算结果中十位上的数字可表示为：a+b 或a+b−10.
故选D.
【点睛】
本题考查列代数式，解答本题的关键是明确题意，列出相应的代数式.
13．
【分析】
从余角的定义出发：两个角和为，则这两个角互余；由此可得解．
【详解】
解：由两个角和为，则这两个角互余可得：
故答案为．
【点睛】
本题考查余角的定义；关键在于知道两个角和为，则这两个角互余．
14．3
【分析】
把十分位上的数字1进行四舍五入即可．
【详解】
解：3.14≈3（精确到个位）．
故答案为3．
【点睛】
本题考查了近似数，近似数与精确数的接近程度，可以用精确度表示．一般有，精确到哪一位，保留几个有效数字等说法．
15．42
【分析】
根据题意的上升和下降列出算式，再进行运算即可．
【详解】
解：根据题意得该无人机现在所在高度为
故答案为42．
【点睛】
本题主要考查了负数的含义和计算，属于基础题型．
16．18
【分析】
由参赛者B的得分就可以得出答对一题的得5分，再由参赛者A，C可知，答错一题扣1分；再根据答对的得分-答错题的得分=88分，建立方程求出其解即可；
【详解】
解：由参赛者B的得分就可以得出答对一题得100÷20=5分，再由参赛者A可知，答错一题扣分=19×5-94=1分；
设D答对的题有x题，则答错的有(20-x)题，
所以5x-(20-x)=88，
解得x=18，
故答案为18．
【点睛】
本题主要考查了一元一次方程的应用（比赛问题）．理解题意，求出积分规则是关键．
17．
【分析】
先容易求得，在根据、分别平分，由图可知所求角等于加上的一半．
【详解】
解：由题可知：

则
因为CM 平分∠ACB，CN平分∠DCE，
则
可得
故答案为
【点睛】
本题主要考察了角平分线的性质；利用角平分线的基本性质来计算角度是关键．
18．1-
【分析】
根据三角形的中线的性质，把三角形面积分成相等的两部分，分别求出△ABP1，△ABP2，△ABP3……△ABPn的面积，即可计算出在第n次后，被剪去图形的面积之和.
【详解】
第一次留下的△ABP1的面积为 ，
第二次留下的△ABP2面积为= ，
第三次留下的△ABP3面积为
……
第n次留下的△ABPn面积为 ，
故在第n次后，被剪去图形的面积之和是1×1- =1- ，
故答案为1-．
【点睛】
本题考查了图形的变化，三角形的面积计算，三角形的中线的性质，以及找规律和简单的计算，解题的关键是根据三角形的中线的性质，把三角形面积分成相等的两部分．
19．（1）0；（2）-8
【分析】
（1）利用有理数运算的去括号法则去括号后合并即可；
（2）根据有理数运算的运算法则和运算顺序依次计算即可.
【详解】
解：（1）
（2）
【点睛】
本题主要考查有理数的混合运算，根据有理数的混合运算法则求解即可.
20．（）．（）
【详解】
试题分析：按照解一元一次方程的步骤解方程即可.
试题解析：
，
，
．

，
，
，
．
点睛:解一元一次方程的一般步骤：去分母，去括号，移项，合并同类项，把系数化为1.
21．-x2+y2，3
【分析】
将代数式去括号，合并同类项，从而将整个代数式化为最简形式，再代入求值即可．
【详解】
解：原式=
=
=
当时，
原式=
【点睛】
本题主要考察了整式的加减运算；关键在于能够正确的去括号、合并同类项．
22．（1）图见解析；（2）图见解析；（3）图见解析．
【分析】
（1）根据射线的定义画出射线AB即可；
（2）根据线段的定义连接BC并延长，然后截取CD=BC即可；
（3）根据两点之间线段最短，连接AC交直线于点E，此时AE+CE最小．
【详解】
（1）如图所示：射线AB即为所求；
（2）如图所示：连接BC并延长线段，然后截取CD=BC，点D即为所求；
（3）如图所示：连接AC交直线于点E，点E即为所求．
【点睛】
本题考查了作图－简单作图，射线、线段的定义及两点之间线段最短的基本事实．
23．（1）每箱香蕉的平均售价是80元；（2）该商家卖完所有香蕉所获利润为4000元.
【分析】
（1）先根据正负数的定义求出每一批的售价，再根据总收入=售价×数量求出总收入，总收入除以总数量即为平均售价,；
（2）用总收入减去总成本即可求出总利润．
【详解】
解：（1）由题意得售价分别为
（元）
（元）
（元）
（元）
（元）
（元）
则总销售额为
=4500+1740+3400+6360
=16000（元）
则平均售价为（元）
答：每箱香蕉的平均售价是80元；
（2）总利润为（元）
答：该商家卖完所有香蕉所获利润为4000元．
【点睛】
本题主要考查正负数的含义及其在实际问题中的应用，正确的理解正负数的定义是解题的关键．
24．（1）（）米；（2）26米．
【分析】
（1）根据题意用代数式表示出宽，继而求出周长；
（2）由条件可得出，，求出周长即可．
【详解】
解：（1）根据题意得：宽为，
则这个长方形的周长为，
（米）；
（2），
∴，，
，，
长方形的周长为（米） ．
【点睛】
此题考查了整式的加减和求代数式的值，熟练掌握整式运算法则是解本题的关键．
25．（1），；（2）；（3）50°或140°．
【分析】
（1）根据，即可求解；
（2）先求出∠COM，再求出∠CON，相加即可求解；
（3）分当OD在内部和外部两种情况分类讨论即可求解．
【详解】
解：（1）∵，
∴，
；
（2）∵平分，
∴,
∵ ，
∴，
∴ ；
（3）如图1，当OD在内部时，
∵，
∴∠BOD=,
∴∠COD=∠BOC-∠BOD=80°-30°=50°；
如图2，当OD在外部时，
∵，
∴∠BOD=,
∴∠COD=∠BOC+∠BOD=80°+60°=140°，
∴的度数为50°或140°．
．
【点睛】
本题考查了角的计算，熟知角的特点和比例意义并根据题意画图求解是解题关键．
26．（1）型车从甲地到乙地的时间为12小时；（2）这批蔬菜共有24吨；（3）单独安排型车运输才能使得本次往返甲乙两地的总费用较少，较少费用为6120元．
【分析】
（1）根据型车与型车行驶路程相同列出方程求解即可；
（2）根据运输蔬菜的车辆数相同列出方程求解即可；
（3）分别计算出两种车辆所需费用，再进行比较即可．
【详解】
解：（1）设型车从甲地到乙地的时间为小时，则

解得，
答：型车从甲地到乙地的时间为12小时；
（2）设蔬菜共有吨，则有，

解得，
答：这批蔬菜共有24吨；
（3）单独使用型车：车量数为：（辆）
冷柜需使用（次）
冷柜使用费用：（元）
路费：（元）
总费用：（元）；
单独使用型车：车量数为：（辆）
冷柜需使用（次）
冷柜使用费用：（元）
路费：（元）
总费用：（元）；
∵
故单独安排型车运输才能使得本次往返甲乙两地的总费用较少，较少费用为6120元．
【点睛】
本题考查了一元一次方程在实际问题中的应用，根据题意，正确列出方程组，是解题的关键．