

-山东省济宁市邹城市2020-2021学年八年级上学期期末数学试卷 (解析版)
展开1.下列图形中,不是轴对称图形的是( )
A.B.C.D.
2.下列运算中,正确的是( )
A.2a+3b=5abB.3x2÷2x=x
C.(x2)3=x6D.(x+y2)2=x2+y4
3.人体中枢神经系统中约含有1千亿个神经元,某种神经元的直径约为52微米,52微米为0.000052米.将0.000052用科学记数法表示为( )
A.5.2×10﹣6B.5.2×10﹣5C.52×10﹣6D.52×10﹣5
4.下列每组数分别是三根小木棒的长度,用它们能摆成三角形的是( )
A.3cm,4cm,8cmB.8cm,7cm,15cm
C.13cm,12cm,20cmD.5cm,5cm,11cm
5.下列各式中从左到右的变形中,是因式分解的是( )
A.(a+3)(a﹣3)=a2﹣9B.a2﹣4a﹣5=a(a﹣4)﹣5
C.a2﹣b2=(a+b)(a﹣b)D.a2﹣4a﹣5=a(a﹣4﹣)
6.如果分式的值为0,那么x的值是( )
A.x=3B.x=±3C.x≠3D.x=﹣3
7.如图,已知△ABC的六个元素,则下面甲、乙、丙三个三角形中和△ABC全等的图形是( )
A.甲和乙B.乙和丙C.只有乙D.只有丙
8.把分式中的x、y的值都扩大到原来的2倍,则分式的值( )
A.不变B.扩大到原来的2倍
C.扩大到原来的4倍D.缩小到原来的
9.如图,AB=BC=CD=DE=EF,如果∠DEF=60°,则∠A的度数为( )
A.20°B.15°C.12°D.10°
10.疫情期间嘉祥外国语学校用4200元钱到商场去购买“84”消毒液,经过协商议价,每瓶便宜1元,结果比用原价多买了140瓶,求原价每瓶多少元?若设原价每瓶x元,则可列出方程为( )
A.﹣=140B.﹣=140
C.﹣=1D.﹣=1
二、填空题(本大题共8个小题,每小题3分,共24分)
11.六边形的内角和等于 度.
12.计算:(2m2n﹣2)2•3m﹣3n3= .
13.如图,在△ABC中,DE是AB的垂直平分线,且分别交AB,AC于点D和E,∠A=50°,∠C=60°,则∠EBC等于 度.
14.分解因式:a﹣ab2= .
15.若9x2+kxy+y2是完全平方式,则k= .
16.如图,在△ABC中,AD为∠BAC的平分线,DE⊥AB于E,DF⊥AC于F,△ABC面积是28cm2,AB=20cm,AC=8cm,则DE的长为 .
17.已知a﹣b=1,则a2﹣b2﹣2b的值是 .
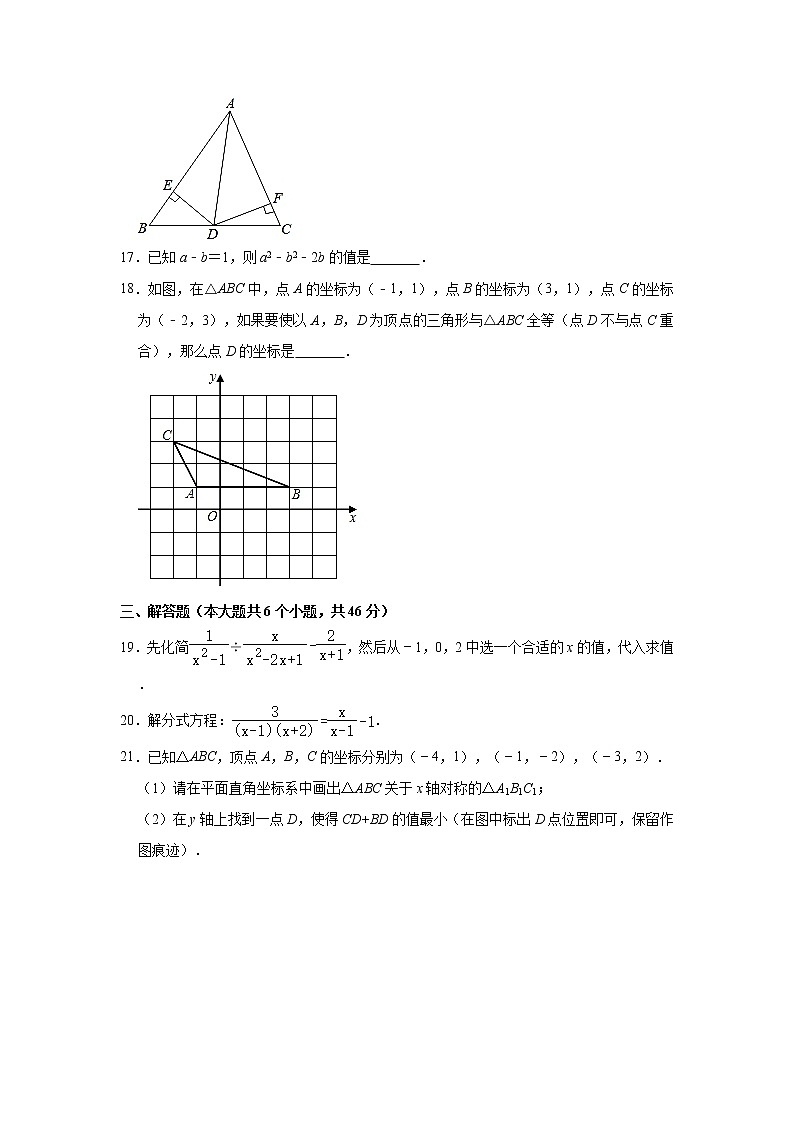
18.如图,在△ABC中,点A的坐标为(﹣1,1),点B的坐标为(3,1),点C的坐标为(﹣2,3),如果要使以A,B,D为顶点的三角形与△ABC全等(点D不与点C重合),那么点D的坐标是 .
三、解答题(本大题共6个小题,共46分)
19.先化简÷,然后从﹣1,0,2中选一个合适的x的值,代入求值.
20.解分式方程:.
21.已知△ABC,顶点A,B,C的坐标分别为(﹣4,1),(﹣1,﹣2),(﹣3,2).
(1)请在平面直角坐标系中画出△ABC关于x轴对称的△A1B1C1;
(2)在y轴上找到一点D,使得CD+BD的值最小(在图中标出D点位置即可,保留作图痕迹).
22.观察下列各式
(x﹣1)(x+1)=x2﹣1
(x﹣1)(x2+x+1)=x3﹣1
(x﹣1)(x3+x2+x+1)=x4﹣1
…
(1)分解因式:x5﹣1= ;
(2)根据规律可得(x﹣1)(xn﹣1+…+x+1)= (其中n为正整数);
(3)计算:(3﹣1)(350+349+348+…+32+3+1).
23.如图,P为等边△ABC的边BC延长线上的一动点,以AP为边向上作等边△APD,连接CD.
(1)求证:△ABP≌△ACD;
(2)当PC=AC时,求∠PDC的度数;
(3)∠PDC与∠PAC有怎样的数量关系?随着点P位置的变化,∠PDC与∠PAC的数量关系是否会发生变化?请说明理由.
24.某水果店一次购进了若干箱蜜桔和苹果,已知购进蜜桔花费800元,购进苹果花费1680元,所购苹果比蜜桔多10箱,苹果每箱的进价是蜜桔每箱进价的1.4倍.
(1)蜜桔和苹果每箱进价分别为多少元?
(2)根据市场情况,每箱苹果可以比每箱蜜桔的利润多5元,这批水果全部售完后,店家若想获得不少于800元的利润,应该如何确定每箱蜜桔和苹果的售价?
参考答案
一、选择题(本大题共10个小题,每小题3分,共30分。在每小题给出的四个选项中只有一个符合题目要求)
1.下列图形中,不是轴对称图形的是( )
A.B.C.D.
【分析】根据关于某条直线对称的图形叫轴对称图形,进而判断得出即可.
解:A、不是轴对称图形,符合题意;
B、是轴对称图形,不合题意;
C、是轴对称图形,不合题意;
D、是轴对称图形,不合题意;
故选:A.
2.下列运算中,正确的是( )
A.2a+3b=5abB.3x2÷2x=x
C.(x2)3=x6D.(x+y2)2=x2+y4
【分析】根据合并同类项,单项式的除法,幂的乘方,完全平方公式进行计算,再选择即可.
解:A、2a+3b不能合并,故错误;
B、3x2÷2x=1.5x,故错误;
C、(x2)3=x6,故正确;
D、(x+y2)2=x2+2xy2+y4,故错误;
故选:C.
3.人体中枢神经系统中约含有1千亿个神经元,某种神经元的直径约为52微米,52微米为0.000052米.将0.000052用科学记数法表示为( )
A.5.2×10﹣6B.5.2×10﹣5C.52×10﹣6D.52×10﹣5
【分析】由科学记数法可知0.000052=5.2×10﹣5;
解:0.000052=5.2×10﹣5;
故选:B.
4.下列每组数分别是三根小木棒的长度,用它们能摆成三角形的是( )
A.3cm,4cm,8cmB.8cm,7cm,15cm
C.13cm,12cm,20cmD.5cm,5cm,11cm
【分析】根据三角形的三边关系“任意两边之和大于第三边,任意两边之差小于第三边”,进行分析.
解:A、3+4<8,不能组成三角形;
B、8+7=15,不能组成三角形;
C、13+12>20,能够组成三角形;
D、5+5<11,不能组成三角形.
故选:C.
5.下列各式中从左到右的变形中,是因式分解的是( )
A.(a+3)(a﹣3)=a2﹣9B.a2﹣4a﹣5=a(a﹣4)﹣5
C.a2﹣b2=(a+b)(a﹣b)D.a2﹣4a﹣5=a(a﹣4﹣)
【分析】根据因式分解的定义逐个判断即可.
解:A.从左到右变形不属于因式分解,故本选项不符合题意;
B.从左到右变形不属于因式分解,故本选项不符合题意;
C.从左到右变形属于因式分解,故本选项符合题意;
D.a2﹣4a﹣5=(a﹣5)(a+1),因式分解是把多项式化成几个整式积的形式,故本选项不符合题意;
故选:C.
6.如果分式的值为0,那么x的值是( )
A.x=3B.x=±3C.x≠3D.x=﹣3
【分析】根据分式值为零的条件可得x﹣3=0且x+3≠0,再解即可.
解:由题意得:x﹣3=0且x+3≠0,
解得:x=3,
故选:A.
7.如图,已知△ABC的六个元素,则下面甲、乙、丙三个三角形中和△ABC全等的图形是( )
A.甲和乙B.乙和丙C.只有乙D.只有丙
【分析】全等三角形的判定定理有SAS,ASA,AAS,SSS,根据定理逐个判断即可.
解:图甲不符合三角形全等的判定定理,即图甲和△ABC不全等;
图乙符合SAS定理,即图乙和△ABC全等;
图丙符合AAS定理,即图丙和△ABC全等;
故选:B.
8.把分式中的x、y的值都扩大到原来的2倍,则分式的值( )
A.不变B.扩大到原来的2倍
C.扩大到原来的4倍D.缩小到原来的
【分析】把分式中的x换成2x,y换成2y,然后根据分式的基本性质进行化简即可.
解:x、y都扩大2倍,==,
所以,分式的值不改变.
故选:A.
9.如图,AB=BC=CD=DE=EF,如果∠DEF=60°,则∠A的度数为( )
A.20°B.15°C.12°D.10°
【分析】根据已知条件,利用等腰三角形和等边三角形的性质及三角形的内角和外角之间的关系进行计算.
解:∵DE=EF,∠DEF=60°,
∴△DEF为等边三角形,
∴∠EDF=60°,
∵AB=BC=CD.
∴△ABC和△BCD为等腰三角形,∠A=∠ACB,∠CBD=∠CDB,
∵∠CBD=∠A+∠ACB=2∠A,
∴∠CDB=2∠A,
∵∠ECD=∠A+∠CDB=3∠A,CD=DE,
∴△CDE为等腰三角形,
∴∠ECD=∠DEC=3∠A,
∠EDF=∠A+∠DEC=4∠A=60°,
∴∠A=15°.
故选:B.
10.疫情期间嘉祥外国语学校用4200元钱到商场去购买“84”消毒液,经过协商议价,每瓶便宜1元,结果比用原价多买了140瓶,求原价每瓶多少元?若设原价每瓶x元,则可列出方程为( )
A.﹣=140B.﹣=140
C.﹣=1D.﹣=1
【分析】设原价每瓶x元,根据关键描述语:“结果比用原价多买了140瓶”得到等量关系:原价买的瓶数﹣实际价格买的瓶数=140,依此列出方程即可.
解:设原价每瓶x元,
根据题意,得﹣=140.
故选:B.
二、填空题(本大题共8个小题,每小题3分,共24分)
11.六边形的内角和等于 720 度.
【分析】n边形的内角和是(n﹣2)•180°,把多边形的边数代入公式,就得到多边形的内角和.
解:(6﹣2)•180=720度,则六边形的内角和等于720度.
12.计算:(2m2n﹣2)2•3m﹣3n3= .
【分析】根据积的乘方和单项式的乘法运算法则,先算乘方,再算乘法.
解:(2m2n﹣2)2•3m﹣3n3=4m4n﹣4•3m﹣3n3=12mn﹣1=.
13.如图,在△ABC中,DE是AB的垂直平分线,且分别交AB,AC于点D和E,∠A=50°,∠C=60°,则∠EBC等于 20 度.
【分析】根据三角形内角和定理求出∠ABC,根据线段垂直平分线的性质得到EA=EB,得到∠EBA=∠A=50°,结合图形计算,得到答案.
解:∵A=50°,∠C=60°,
∴∠ABC=180°﹣50°﹣60°=70°,
∵DE是AB的垂直平分线,
∴EA=EB,
∴∠EBA=∠A=50°,
∴∠EBC=∠ABC﹣∠EBA=70°﹣50°=20°,
故答案为:20.
14.分解因式:a﹣ab2= a(1+b)(1﹣b) .
【分析】先提取公因式a,再对余下的多项式利用平方差公式继续分解.
解:原式=a(1﹣b2)
=a(1+b)(1﹣b).
故答案为:a(1+b)(1﹣b).
15.若9x2+kxy+y2是完全平方式,则k= ±6 .
【分析】根据完全平方式得出kxy=±2•3x•y,求出即可.
解:∵9x2+kxy+y2是完全平方式,
∴kxy=±2•3x•y,
解得:k=±6,
故答案为:±6.
16.如图,在△ABC中,AD为∠BAC的平分线,DE⊥AB于E,DF⊥AC于F,△ABC面积是28cm2,AB=20cm,AC=8cm,则DE的长为 2cm .
【分析】先根据角平分线的性质得出DE=DF,再根据三角形的面积公式即可得出结论.
解:∵在△ABC中,AD为∠BAC的平分线,DE⊥AB于E,DF⊥AC于F,
∴DE=DF,
∴S△ABC=S△ABD+S△ACD=AB•DE+AC•DF,
∵△ABC面积是28cm2,AB=20cm,AC=8cm,
∴×20DE+×8DF=10DE+4DF=14DE=28,解得DE=2cm.
故答案为:2cm.
17.已知a﹣b=1,则a2﹣b2﹣2b的值是 1 .
【分析】由已知得a=b+1,代入所求代数式,利用完全平方公式计算.
【解答】:∵a﹣b=1,
∴a=b+1,
∴a2﹣b2﹣2b=(b+1)2﹣b2﹣2b=b2+2b+1﹣b2﹣2b=1.
故答案为:1.
18.如图,在△ABC中,点A的坐标为(﹣1,1),点B的坐标为(3,1),点C的坐标为(﹣2,3),如果要使以A,B,D为顶点的三角形与△ABC全等(点D不与点C重合),那么点D的坐标是 (﹣2,﹣1)或(4,3)或(4,﹣1) .
【分析】根据题意画出图形,根据A、B、C的坐标和全等三角形的性质即可得出答案.
解:符合题意的有3个,如图,
∵点A、B、C坐标为(﹣1,1),(3,1),(﹣2,3),
∴D1的坐标是(﹣2,﹣1),D2的坐标是(4,3),D3的坐标是(4,﹣1),
故答案为:(﹣2,﹣1)或(4,3)或(4,﹣1).
三、解答题(本大题共6个小题,共46分)
19.先化简÷,然后从﹣1,0,2中选一个合适的x的值,代入求值.
【分析】先根据分式混合运算顺序和运算法则化简原式,再由分式有意义的条件选取合适的x的值代入计算可得.
解:原式=•﹣
=﹣
=
=﹣,
当x=2时,原式=﹣.
20.解分式方程:.
【分析】分式方程去分母转化为整式方程,求出整式方程的解得到x的值,经检验即可得到分式方程的解.
解:去分母得:3=x2+2x﹣x2﹣x+2,
解得:x=1,
经检验x=1是增根,分式方程无解.
21.已知△ABC,顶点A,B,C的坐标分别为(﹣4,1),(﹣1,﹣2),(﹣3,2).
(1)请在平面直角坐标系中画出△ABC关于x轴对称的△A1B1C1;
(2)在y轴上找到一点D,使得CD+BD的值最小(在图中标出D点位置即可,保留作图痕迹).
【分析】(1)作出A,B,C的对应点A1,B1,C1即可.
(2)作点B关于y轴的对称点B′,连接CB′交y轴于D,连接BD,点D即为所求作.
解:(1)如图,△A1B1C1即为所求作.
(2)如图,点D即为所求作.
22.观察下列各式
(x﹣1)(x+1)=x2﹣1
(x﹣1)(x2+x+1)=x3﹣1
(x﹣1)(x3+x2+x+1)=x4﹣1
…
(1)分解因式:x5﹣1= (x﹣1)(x4+x3+x2+x+1) ;
(2)根据规律可得(x﹣1)(xn﹣1+…+x+1)= xn﹣1 (其中n为正整数);
(3)计算:(3﹣1)(350+349+348+…+32+3+1).
【分析】(1)观察各式,得到因式结果即可;
(2)利用得出的规律计算即可;
(3)利用得出的规律计算即可得到结果.
解:(1)原式=(x﹣1)(x4+x3+x2+x+1);
(2)(x﹣1)(xn﹣1+…+x+1)=xn﹣1;
(3)原式=351﹣1.
故答案为:(1)(x﹣1)(x4+x3+x2+x+1);(2)xn﹣1
23.如图,P为等边△ABC的边BC延长线上的一动点,以AP为边向上作等边△APD,连接CD.
(1)求证:△ABP≌△ACD;
(2)当PC=AC时,求∠PDC的度数;
(3)∠PDC与∠PAC有怎样的数量关系?随着点P位置的变化,∠PDC与∠PAC的数量关系是否会发生变化?请说明理由.
【分析】(1)根据SAS证明三角形证明即可.
(2)证明∠APC=30°,再利用全等三角形的性质解决问题即可.
(3)结论:∠PDC=∠PAC.证明△CPA≌△TPD(SAS),可得结论.
【解答】(1)证明:∵△ABC,△ADP是等边三角形,
∴AB=AC,AP=AD,∠BAC=∠PAD=60°,
∴∠BAP=∠CAD,
在ABP和△ACD中,
,
∴△ABP≌△ACD(SAS).
(2)解:∵△ACB是等边三角形,
∴∠ACB=60°,
∵CA=CP,
∴∠CAP=∠CPA,
∵∠ACB=∠CAP+∠CPA,
∴∠CPA=∠CAP=30°,
∵△ABP≌△ACD,
∴∠APB=∠ADC=30°,
∵∠ADP=60°
∴∠PDC=∠ADP﹣∠ADC=30°.
(3)结论:∠PDC=∠PAC.
理由:设AP交CD于O,在CD上截取点T,使得CT=CP,连接PT.
∵△ABP≌△ACD,
∴∠APB=∠ADC,
∵∠AOD=∠COP,
∴∠OCP=∠DAP,
∵△ADP是等边三角形,
∴∠DAP=∠APD=60°,PA=PD,
∴∠PCT=60°,
∵CT=CP,
∴△CPT是等边三角形,
∴∠CPT=∠APD=60°,PC=PT,
∴∠CPA=∠TPD,
在△CPA和△TPD中,
,
∴△CPA≌△TPD(SAS),
∴∠CDP=∠CAP.
24.某水果店一次购进了若干箱蜜桔和苹果,已知购进蜜桔花费800元,购进苹果花费1680元,所购苹果比蜜桔多10箱,苹果每箱的进价是蜜桔每箱进价的1.4倍.
(1)蜜桔和苹果每箱进价分别为多少元?
(2)根据市场情况,每箱苹果可以比每箱蜜桔的利润多5元,这批水果全部售完后,店家若想获得不少于800元的利润,应该如何确定每箱蜜桔和苹果的售价?
【分析】(1)设蜜桔每箱x元,则苹果每箱1.4x元,由题意列出分式方程,解方程即可;
(2)设蜜桔每箱利润y元,则苹果每箱利润(y+5)元,由题意列出不等式,解不等式即可.
解:(1)设蜜桔每箱x元,则苹果每箱1.4x元,
根据题意得:,
解得:x=40,
经检验x=40是原方程的解,
则1.4x=1.4×40=56,
答:蜜橘和苹果每箱进价分别为40元和56元;
(2)设蜜桔每箱利润y元,则苹果每箱利润(y+5)元,
根据题意得:,
解得:y≥13,
13+40=53,13+5+56=74,
答:每箱蜜桔和苹果的售价分别不少于53元和74元.
2023-2024学年山东省济宁市邹城市八年级(上)期中数学试卷(含解析): 这是一份2023-2024学年山东省济宁市邹城市八年级(上)期中数学试卷(含解析),共18页。试卷主要包含了选择题,填空题,解答题等内容,欢迎下载使用。
2022-2023学年山东省济宁市邹城市八年级(上)期末数学试卷(含解析): 这是一份2022-2023学年山东省济宁市邹城市八年级(上)期末数学试卷(含解析),共14页。试卷主要包含了选择题,填空题,计算题,解答题等内容,欢迎下载使用。
2022-2023学年山东省济宁市邹城市八年级(下)期末数学试卷(含解析): 这是一份2022-2023学年山东省济宁市邹城市八年级(下)期末数学试卷(含解析),共23页。试卷主要包含了选择题,填空题,解答题等内容,欢迎下载使用。












