




初中数学湘教版七年级下册6.1.1平均数精品课件ppt
展开1.掌握算术平均数的概念,会求一组数据的算术平均数.(重点)2.会用算术平均数解决实际生活中的问题;(难点)3.学会用计算器求平均数.
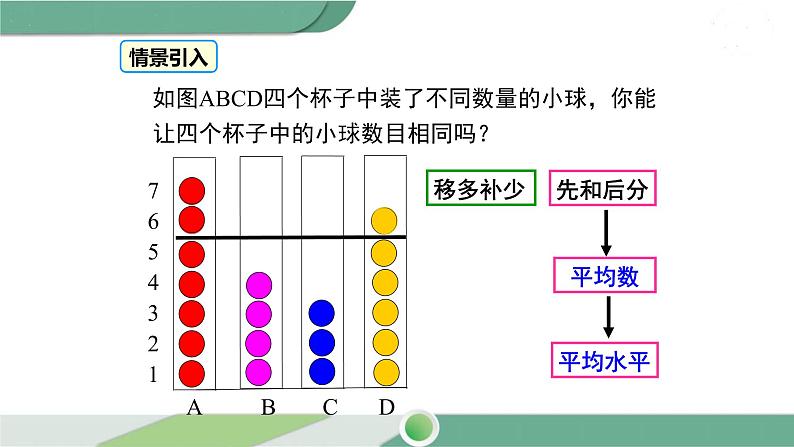
A B C D
如图ABCD四个杯子中装了不同数量的小球,你能让四个杯子中的小球数目相同吗?
问题:当你听到“小亮的身高在班上是中等偏上的”,“A 篮球队队员比B 队更年轻”等诸如此类的说法时,你思考过这些话的含义吗?你知道人们是如何作出这一判断的吗?
数学上,我们常借助平均数、中位数、众数、方差等来对数据进行分析和刻画.
问题1:2017年重庆7月中旬一周的每天最高气温如下:
你能快速计算这一周的平均最高气温吗?
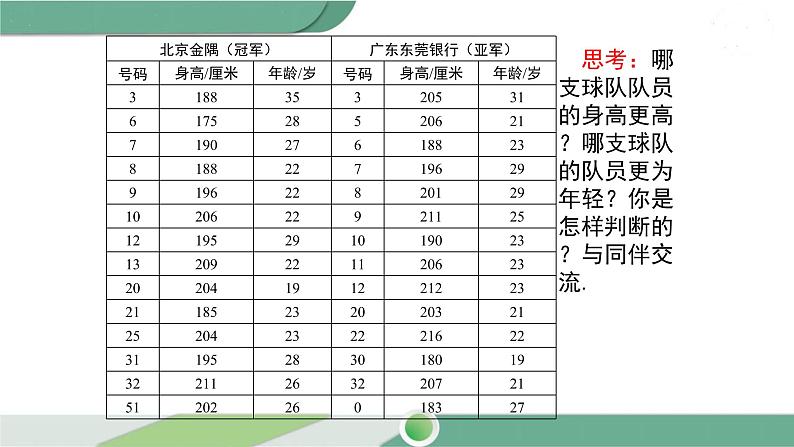
影响一场比赛的成绩有哪些因素? 如何衡量两个球队队员的身高? 怎样理解“甲队队员的身高比乙队更高”? 要比较两个球队队员的身高,需要收集哪些 数据呢?
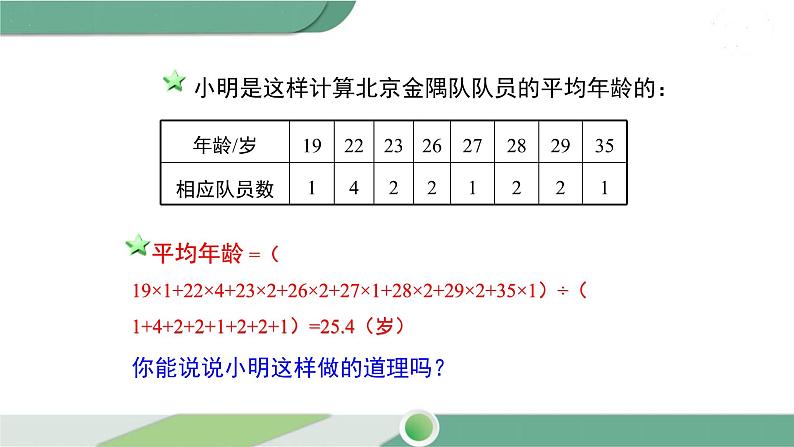
思考:哪支球队队员的身高更高?哪支球队的队员更为年轻?你是怎样判断的?与同伴交流.
问题2 一个小组10名同学的身高(单位:cm)如下表所示:
(1)计算10名同学身高的平均数.
平均数=(151+156+153+158+154+161+155+157+154+157)÷10= 155.6(cm)
(2)在数轴上标出表示这些同学的身高及其平均数的点.
(3)考察表示平均数的点与其他的点的位置关系,你能得出什么结论?
平均数的大小与一组数据的每个数据都有关系,如果这组数据中的一个数据变大,其平均数将变大;若这组数据中的一个数据变小,平均数将变小.
思考1:通过上述问题,平均数与数据组有什么关系?
平均数作为一组数据的一个代表值,它刻画了这组数据的平均水平.
思考2:平均数的作用和特点吗?
平均数是一组数据的数值大小的集中代表值,它刻画了这组数据整体的平均状态,体现了这组数据的整体性质,对于这组数据的个体性质不能作出什么结论.
例1 植树节到了, 某单位组织职工开展植树竞赛, 下图反映的是植树量与人数之间的关系.
请根据图中信息计算:(1)总共有多少人参加了本次活动?(2)总共植树多少棵?(3)平均每人植树多少棵?
解:(1)参加本次活动的总人数是1+8+1+10+8+3+1=32(人)(2)总共植树3×8+4×1+5×10+6×8+7×3+8×1=155(棵).(3)平均每人植树 (棵)
某班级为了解同学年龄情况,作了一次年龄调查,结果如下:13岁8人,14岁16人,15岁24人,16岁2人.求这个班级学生的平均年龄(结果取整数).
解:这个班级学生的平均年龄为:
所以,他们的平均年龄约为14岁.
例1 某农业技术员试种了三个品种的棉花各10株. 秋收时他清点了这30株棉花的结桃数如下表:
分析平均数可以作为一组数据的代表值,它刻画了这组数据的平均水平.当我们要比较棉花的品种时,可以计算出这些棉花结桃数的平均数,再通过平均数来进行比较.
解:设甲、乙、丙三个品种的平均结桃数分别为
由于甲种棉花的平均结桃数高于其他两个品种的平均结桃数,所以我们可以认为甲种棉花较好.
例2 个体户张某经营一家餐馆,下面是该餐馆所有工作人员2000年10月份的工资:
张某: 4000元;会计:700元;厨师甲:1000元;乙:900元;杂工甲:580元;乙:560元;服务员甲:620元;乙:600元;丙:580元
(1)计算他们的平均工资,这个平均工资能否反映餐馆加工在这个月收入的一般水平?
(2)不计张某的工资,再求餐馆员工的月平均工资,这个平均工资能代表一般水平吗?
思考:通过这个问题,说出平均数有什么缺点吗?如何避免这个缺点?
为了消除这个缺点,当出现这种情形时,可以将特殊数据去掉.如某些评奖比赛的计分,通常去掉一个最高分和一个最低分.
平均数容易受个别特殊数据的影响.
例如:在全校歌咏比赛中,7位评委给一个班级的打分分别是:
9.00,8.00,9.10,9.10,9.15,9.00,9.58.
但实际上评委的评判受主观因素影响比较大,评分也比较悬殊,为了消除极端数对平均数的影响,一般去掉一个最高分和一个最低分,取最后得分
这个分数才比较合理地反映了这个班级的最后得分.
你可以根据计算器使用说明书动手试一试,了解这样修改已经输入的数据,怎样简便输入多个相同的数据.
用计算器求八年级各班学生的平均数
1.某商场用单价5元糖果1千克, 单价7元的糖果2千克,单价8元的糖果5千克, 混合为什锦糖果销售, 那么这种什锦果的单价是______. (保留1位小数)
2. 某次数学测验成绩统计如下: 得100分3人, 得95分5人,得90分6人, 得80分12人,得70分16人, 得60分5人, 则该班这次测验的平均得分是______.
3. 有20个机器零件,测得质量分别如下:(单位:g)
22.5,22.7,22.8,22.7,22.522.9,23.0,23.4,23.2,23.322.5,22.7,22.8,22.5,22.923.0,23.4,23.2,22.7,23.3
试计算机器零件质量的平均数.
机器零件质量的平均数为22.9 .
4.如果公司想招一名综合能力较强的翻译,请计算两名应试者的平均成绩,应该录用谁?
显然甲的成绩比乙高,所以从成绩看,应该录取甲.
1.已知:x1,x2,x3,…, x10的平均数是a,x11,x12,x13,… ,x30的平均数是b,则x1,x2,x3,… ,x30的平均数( )A.(a+b) B.(a+b) C.(a+3b)/3 D.(a+2b)/3
2.若x1,x2,…, xn的平均数为a, (1)则数据x1+3,x2+3,…,xn+3的平均数为 . (2)则数据10x1,10x2,… ,10xn 的平均数为 .
湘教版七年级下册6.1.1平均数教学演示ppt课件: 这是一份湘教版七年级下册<a href="/sx/tb_c95294_t3/?tag_id=26" target="_blank">6.1.1平均数教学演示ppt课件</a>,共25页。PPT课件主要包含了算术平均数,计算公式,计算器操作,读信息,议一议,884分,选手B等内容,欢迎下载使用。
初中数学6.1.1平均数评课ppt课件: 这是一份初中数学<a href="/sx/tb_c95294_t3/?tag_id=26" target="_blank">6.1.1平均数评课ppt课件</a>,共23页。PPT课件主要包含了哪个品种较好,答不一定,平均数,计算公式,计算器求平均数等内容,欢迎下载使用。
初中数学湘教版七年级下册6.1.1平均数习题ppt课件: 这是一份初中数学湘教版七年级下册6.1.1平均数习题ppt课件














