北师大版八年级下册3 三角形的中位线评优课课件ppt

这是一份北师大版八年级下册3 三角形的中位线评优课课件ppt，共15页。PPT课件主要包含了学习目标，课堂学习，课堂小结，当堂检测等内容，欢迎下载使用。

经历探索三角形中位线定理的过程，发展合情推理能力。
证明三角形中位线定理，发展演绎推理能力；运用三角形中位线定理解决简单问题
 Life isn't abut waiting fr the strm t pass. it's abut learning t dance
你能将任意一个三角形分成四个全等的三角形吗？你能通过剪拼的方式，将一个三角形拼成一个与其面积相等的平行四边形吗？你能猜想出三角形两边中点的连线与第三边有怎样的关系？你能证明你的猜想吗？
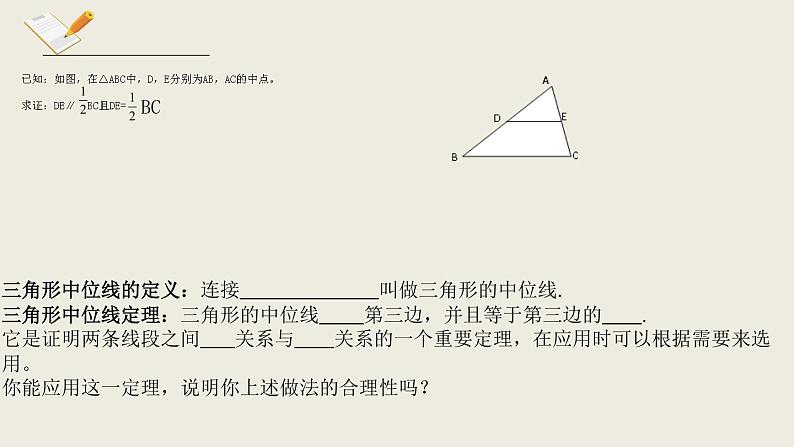
已知：如图，在△ABC中，D，E分别为AB，AC的中点。求证：DE∥
三角形中位线的定义：连接 叫做三角形的中位线.三角形中位线定理：三角形的中位线 第三边，并且等于第三边的 .它是证明两条线段之间 关系与 关系的一个重要定理，在应用时可以根据需要来选用。你能应用这一定理，说明你上述做法的合理性吗？
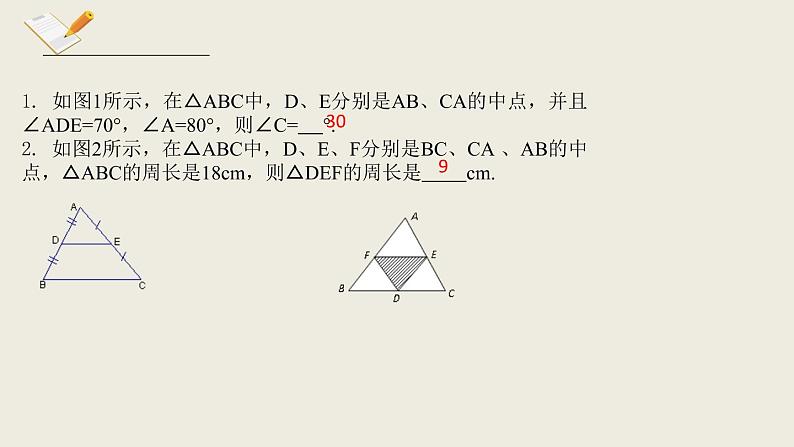
1. 如图1所示，在△ABC中，D、E分别是AB、CA的中点，并且∠ADE=70°，∠A=80°，则∠C= °.2. 如图2所示，在△ABC中，D、E、F分别是BC、CA 、AB的中点，△ABC的周长是18cm，则△DEF的周长是 cm.
3．如图3，在四边形ABCD中，已知AB＝CD，M、N、P分别是AD、BC、BD的中点，∠ABD＝20°，∠BDC＝70°，则∠NMP的度数为 .
【例1】如图4，点E、F、G、H分别为四边形ABCD的边AB、BC、CD、AD的中点，试判断四边形EFGH的形状，并说明理由．
归纳与小结：1.在此四边形问题的解决中，依然运用了 思想，将四边形问题 成三角形问题，具体做法为连接 ；2.本例中点四边形EFGH称作“中点四边形”，由此我们可以得到结论：任意四边形的中点四边形的形状都是 .
【例2】求证：三角形的一条中位线与第三边上的中线互相平分.已知：如图，△ABC的中，D、E分别是边AB、AC的中点，AF是BC边上的中线求证： DE与AF互相平分
1.三角形中位线的定义：连接 叫做三角形的中位线；2.三角形中位线定理：三角形的中位线 第三边，并且等于第三边的 ；它是证明两条线段之间 关系与 关系的一个重要定理，在应用时可以根据需要来选用。3．平行四边形的中点四边形是 .
1．如图，在△ABC中，D是AB上一点，AD=AC，AE⊥CD，垂足为点E，F是BC的中点，若BD=16，则EF的长为(　　)A．32B．16C．8D．4
2．在△ABC中，D、E分别是BC、AC中点，BF平分∠ABC．交DE于点F．AB＝8，BC＝6，则EF的长为（　　）A．1B．2C．3D．4