初中数学北师大版八年级下册3 线段的垂直平分线完美版课件ppt

这是一份初中数学北师大版八年级下册3 线段的垂直平分线完美版课件ppt，共25页。PPT课件主要包含了P1AP1B，P2AP2B，P3AP3B，P1A与P1B，P2A与P2B，P3A与P3B，课堂练习，议一议，∴∠1∠B，∴∠CAF∠B等内容，欢迎下载使用。
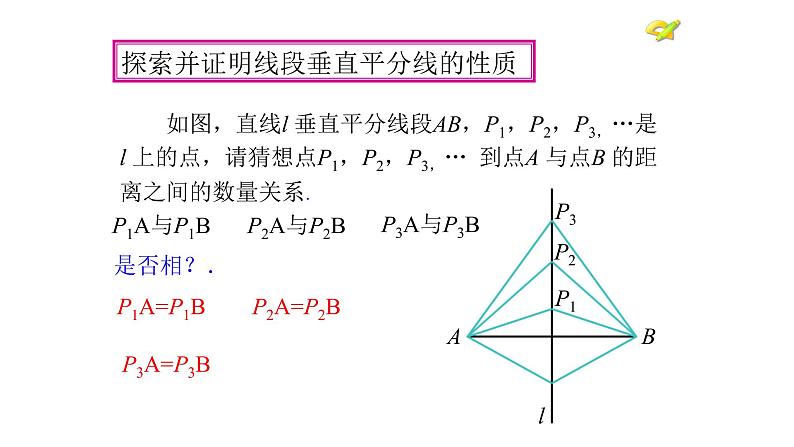
探索并证明线段垂直平分线的性质
　　如图，直线l 垂直平分线段AB，P1，P2，P3，…是l 上的点，请猜想点P1，P2，P3，… 到点A 与点B 的距离之间的数量关系．
线段垂直平分线的性质：
定理：线段垂直平分线上的点到线段两个端点的距离相等．
已知：如图，直线MN⊥AB，垂足是C，且AC=BC，P是MN上的点．求证：PA=PB．
证明：∵MN⊥AB， ∴∠PCA=∠PCB=90° ∵AC=BC，PC=PC, ∴△PCA≌△PCB(SAS) ； ∴PA=PB(全等三角形的对应边相等)．
你能写出上面这个定理的逆命题吗?它是真命题吗?
如果有一个点到线段两个端点的距离相等，那么这个点在这条线段的垂直平分线上．即到线段两个端点的距离相等的点在这条线段的垂直平分线上．
当我们写出逆命题时，就想到判断它的真假．如果真，则需证明它；如果假，则需用反例说明．
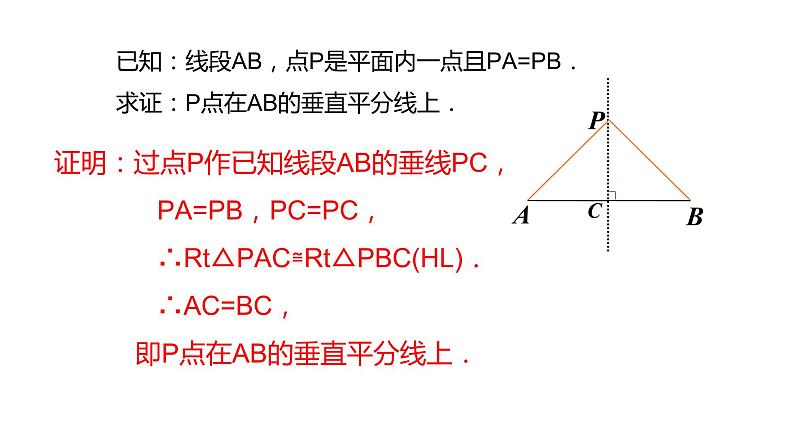
已知：线段AB，点P是平面内一点且PA=PB．求证：P点在AB的垂直平分线上．
证明：过点P作已知线段AB的垂线PC， PA=PB，PC=PC， ∴Rt△PAC≌Rt△PBC(HL)． ∴AC=BC， 即P点在AB的垂直平分线上．
证法二：取AB的中点C，过P,C作直线． ∵AP=BP，PC=PC.AC=CB， ∴△APC≌△BPC(SSS)． ∴∠PCA=∠PCB(全等三角形的对应角相等) 又∵∠PCA+∠PCB=180°， ∴∠PCA=∠PCB=∠90°，即PC⊥AB ∴P点在AB的垂直平分线上．
证法三：过P点作∠APB的角平分线交AB于点C．
探索并证明线段垂直平分线的判定
　　用数学符号表示为：∵　PA =PB，∴　点P 在AB 的垂直平分线上．
　　与一条线段两个端点距离相等的点，在这条线段的垂直平分线上．
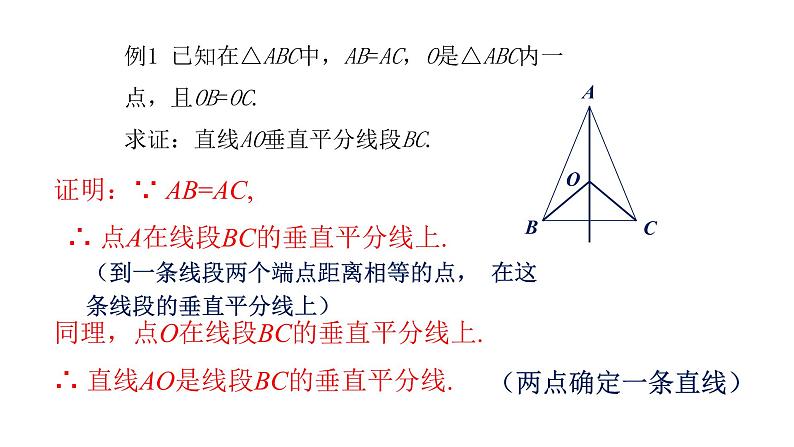
例1 已知在△ABC中，AB=AC，O是△ABC内一 点，且OB=OC.求证：直线AO垂直平分线段BC.
证明：∵ AB=AC, ∴ 点A在线段BC的垂直平分线上. 同理，点O在线段BC的垂直平分线上.∴ 直线AO是线段BC的垂直平分线.
（到一条线段两个端点距离相等的点， 在这条线段的垂直平分线上）
【例2】如图，在Rt△ABC中，∠C＝90°，∠CAB的平分线AD交BC于点D，若DE垂直平分AB，求∠B的度数．
1.如图，在△ABC中，AB＝BC，∠ABC＝110°，AB的垂直平分线DE交AC于点D，连接BD，求∠ABD的度数．
解：∵　AD⊥BC，BD =DC ∴　AD 是BC 的垂直平分线 ∴　AB =AC∵　点C 在AE 的垂直平分线上∴　AC =CE． ∴　AB =AC =CE
2　如图，AD⊥BC，BD =DC，点C 在AE 的垂直平分线上，AB，AC，CE 的长度有什么关系？AB+BD与DE 有什么关系？
∵　AB =CE，BD =DC，∴　AB +BD =CD +CE． 即　AB +BD =DE ．
3．如图，在△ABC中，∠C＝90°，∠B＝15°，AB的垂直平分线交BC于点D，交AB于点E，DB＝10.求∠ADC的度数和边AC的长．
4．如图，在△ABC中，AB的垂直平分线MN交AB于点D，交AC于点E，且AC＝15 cm，△BCE的周长等于25 cm.(1)求BC的长；(2)若∠A＝36°，AB＝AC，求证：BC＝BE.
解：∵DE是AB的垂直平分线，∴AE＝BE.∵△BCE的周长等于25 cm.∴BE＋EC＋BC＝25 cm，∴AE＋EC＋BC＝25 cm，即AC＋BC＝25 cm.∵AC＝15 cm，∴BC＝10 cm.
(2)证明：∵AB＝AC，∠A＝36°，∴∠ABC＝∠C＝72°.∵DE是AB的垂直平分线，∴AE＝BE，∴∠A＝∠ABE＝36°，∴∠BEC＝∠A＋∠ABE＝72°，∴∠C＝∠BEC，∴BC＝BE.
1.3线段的垂直平分线第二课时
例：证明结论：三角形三边的垂直平分线交于一点.
已知：在△ABC中，设AB、BC的垂直平分线交于点O.求证：O点在AC的垂直平分线上．
证明：连接AO，BO，CO． ∵点O在线段AB的垂直平分线上， ∴OA=OB(线段垂直平分线上的点到线 段两个端点的距离相等)． 同理OB=OC．∴OA=OC． ∴O点在AC的垂直平分线上(到线段两个端点距离相等的点.在这条线段的垂直平分线上)． ∴AB、BC、AC的垂直平分线相交于点O
定理:三角形三条边的垂直平分线相交于一点,并且这一点到三个顶点的距离相等。
如图,在△ABC中,∵c,a,b分别是AB,BC,AC的垂直平分线(已知),∴c,a,b相交于一点P,且PA=PB=PC(三角形三条边的垂直平分线相交于一点,并且这一点到三个顶点的距离相等).
这是一个证明三条直线交于一点的证明根据。
(1)已知三角形的一条边及这条边上的高，你能作出三角形吗?如果能，能作几个?所作出的三角形都全等吗?
已知：三角形的一条边a和这边上的高h求作：△ABC，使BC=a，BC边上的高为h
这样的三角形有无数多个．观察还可以发现这些三角形不都全等．
(2)已知等腰三角形的底边及底边上的高，你能用尺规作出等腰三角形吗?能作几个?
这样的等腰三角形应该只有两个，并且它们是全等的，分别位于已知底边的两侧． 你能尝试着用尺规作出这个三角形吗?
例2已知底边及底边上的高，求作等腰三角形．已知：线段a、h求作：△ABC，使AB=AC，BC=a，高AD=h作法：1．作BC=a； 2．作线段BC的垂直平分线MN交BC 于D点； 3．以D为圆心，h长为半径作弧交MN于A点； 4．连接AB、AC ∴△ABC就是所求作的三角形
解：如图，连接AD.∵AB的垂直平分线交AB于点E，∴AD＝BD.设BD＝x，则AD＝x，CD＝4－x.在Rt△ACD中，∵AC＝3，CD＝4－x，AD＝x，∴AC2＋CD2＝AD2，即32＋(4－x)2＝x2，
1．如图，△ABC中，∠C＝90°，AC＝3，BC＝4，AB的垂直平分线交AB于点E，交BC于点D，求BD的长．
解得x＝ ，即BD＝
2．如图，已知AB比AC长3 cm，BC的垂直平分线交AB于点D，交BC于点E，△ACD的周长是15 cm，求AB和AC的长．
3．在△ABC中，∠BAC＝140°，BC＝12，AB，AC的垂直平分线分别交BC于点E，F，求∠EAF的度数和△AEF的周长．
解：∵AB，AC的垂直平分线分别交BC于点E，F，∴AE＝BE，AF＝CF，∴△AEF的周长＝AE＋AF＋EF＝BE＋EF＋CF＝BC＝12.∵△ABC中，∠BAC＝140°，∴∠B＋∠C＝180°－∠BAC＝40°.∵AE＝BE，AF＝CF，∴∠BAE＝∠B，∠CAF＝∠C，∴∠BAE＋∠CAF＝∠B＋∠C＝40°，∴∠EAF＝∠BAC－(∠BAE＋∠CAF)＝100°.
4.已知:如图,AD平分∠BAC,EF垂直平分AD交BC的延长线于F,连结AF.求证: ∠CAF= ∠B.
证明:∵ EF垂直平分AD(已知)
∴ AF=DF(线段垂直平分线的性质定理)
∴∠1+ ∠ 2= ∠4(等边对等角)
又∵∠ 4=∠B+∠3(三角形的一个外角等于与它不相邻的两个内角的和)
∵ AD平分∠BAC(已知) ∴∠ 2=∠3(角平分线的定义)
∠1+ ∠ 2=∠B+∠3
5. 如图，△ABC的外角∠DAC的平分线交BC边的垂直平分线PQ于点P，PD⊥AB于点D.(1)过点P作PE⊥AC于点E，求证：BD＝CE；(2)若AB＝6 cm，AC＝10 cm，求AD的长．
解：(1)∵PQ是BC边的垂直平分线，∴PB＝PC，∵AP平分∠DAC，PD⊥AB，PE⊥AC，∴∠DAP＝∠EAP，∠PDA＝∠PEA＝90°，AP＝AP，∴△PAD≌△PAE(AAS)，∴PD＝PE，在Rt△BPD和Rt△CPE中，PD＝PE，PB＝PC，∴Rt△BPD≌Rt△CPE(HL)，∴BD＝CE(2)由(1)知△PAD≌△PAE，∴AD＝AE，∴AD＋6＝10－AD，解得AD＝2 cm