北师大版七年级下册3 用图象表示的变量间关系获奖ppt课件

这是一份北师大版七年级下册3 用图象表示的变量间关系获奖ppt课件，共18页。PPT课件主要包含了①三角，②三边，③两角一边，探索三角形全等的条件，④两边一角，5cm，ACDF，ABDE，∠A＝∠D，SAS等内容，欢迎下载使用。

④两边一角有二种情况；
如果满足三个条件，画出的三角形一定全等吗？
（1）两边及其夹角（2）两边和其中一边的对角
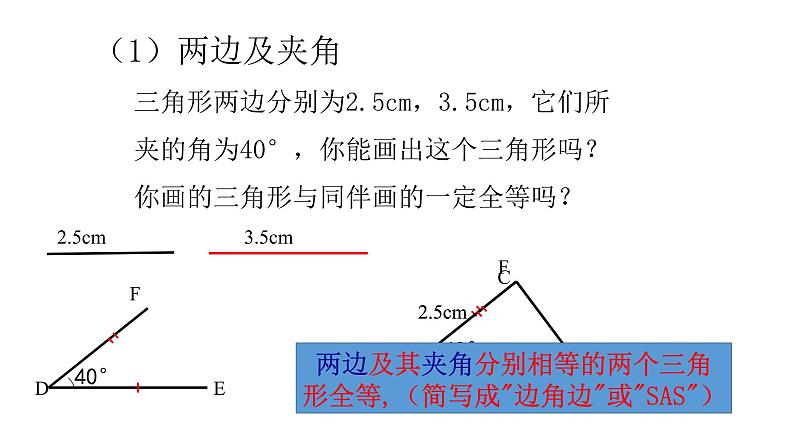
（1）两边及夹角 三角形两边分别为2.5cm，3.5cm，它们所 夹的角为40°，你能画出这个三角形吗？ 你画的三角形与同伴画的一定全等吗？
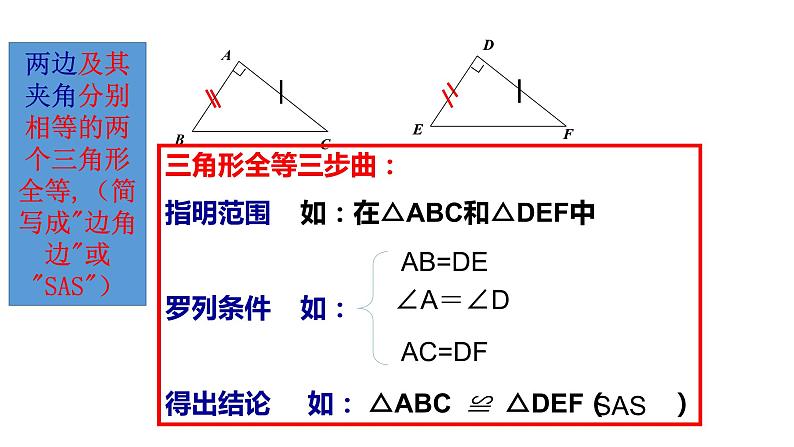
两边及其夹角分别相等的两个三角形全等,（简写成"边角边"或"SAS"）
三角形全等三步曲：指明范围 如：在△ABC和△DEF中罗列条件 如：得出结论 如： △ABC ≌ △DEF（ ）
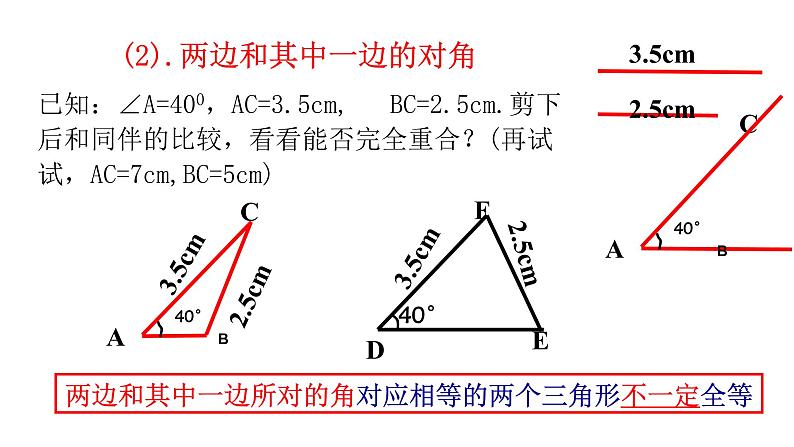
(2).两边和其中一边的对角
两边和其中一边所对的角对应相等的两个三角形不一定全等
已知：∠A=400，AC=3.5cm, BC=2.5cm.剪下后和同伴的比较，看看能否完全重合？(再试试，AC=7cm,BC=5cm)
1. 今天我们学习哪种方法判定两三角形全等？
边角边（SAS）
2. 通过这节课，判定三角形全等的条件有哪些？
SSS，SAS，ASA，AAS
3.在这四种说明三角形全等的条件中，你发现了什么？
至少有一个条件：边相等
“边边角”不能判定两个三角形全等
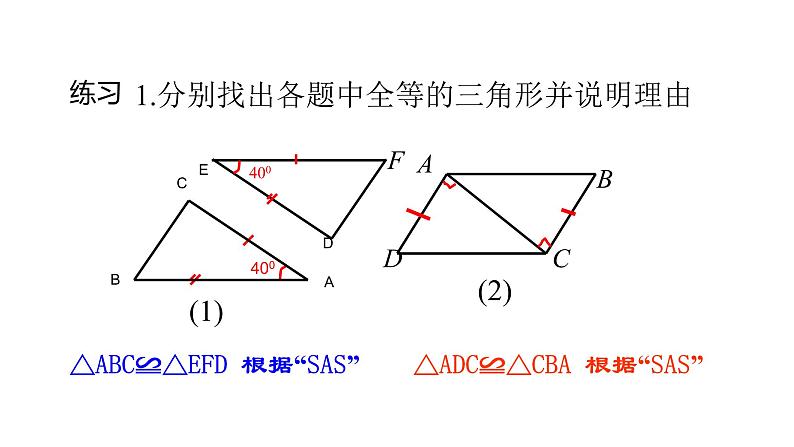
1.分别找出各题中全等的三角形并说明理由
△ADC≌△CBA 根据“SAS”
△ABC≌△EFD 根据“SAS”
小明做了一个如图所示的风筝，其中∠EDH=∠FDH, ED=FD ，将上述条件标注在图中，小明不用测量就能知道EH=FH吗？
在△HED和 △HFD中，
△HED ≌ △HFD （SAS）
如图，在一个风筝ABCD中，AB=AD,BC=DC分别在AB,AD的中点E,F处挂两根彩线EC,FC,试说明;EC=FC
在△ABC和△ADC中，
∴△ABC≌△ADC(SSS),
∴∠EAC=∠FAC.∵E,F分别是AB ,AD的中点，
AE= AB, AF= AD.
在△AEC和△AFC中，∠EAC=∠FAC,AC=AC,AE=AF,∴△AEC≌△AFC(SAS),
1.已知：如图，AD∥BC，AD=CB， 求证：DC=BA.
【证明】∵ AD∥BC, ∴ ∠1=∠2（两直线平行，内错角相等）. 在△DAC和△BCA中,
2，如图，已知AB＝AC，AD＝AE。求证：∠B＝∠C
证明：在△ABD和△ACE中
∴△ABD≌△ACE（SAS）∴∠B＝∠C（全等三角形 对应角相等）
例1：如图，已知△ABC中，BE和CD分别为∠B和∠C的平分线，且BD = CE，∠1 = ∠2.求证：BE = CD
证明：∵∠DBC = 2∠1，∠ECB = 2∠2 （角平分线的定义） ∠1 = ∠2 ∴∠DBC = ∠ECB
∵在△DBC和△ECB中 BD = CE ∠DBC = ∠ECB BC = CB（公共边）
∴ △DBC≌△ECB（SAS）∴BE = CD（全等三角形的对应边相等）
如图，∠B＝∠E，AB＝EF，BD＝EC，那么△ABC与△FED全等吗？为什么？
AC∥FD吗？为什么？
在△ABC与△FED中
解：全等。∵BD=EC　 ∴BD－CD＝EC－CD。即BC＝ED　　
∴△ABC≌△FED（SAS）
（全等三角形对应角相等）
（内错角相等，两直线平行）
1.如图所示，OD=OB，AD∥BC，则全等三角形有( )(A)2对 (B)3对(C)4对 (D)5对【解析】选C.根据题意AD∥BC得∠ADO=∠CBO，∠DOA=∠BOC，又OD=OB，所以△DOA≌△BOC同理可证△DOC≌△BOA，△DAB≌△BCD，△ACD≌△CAB，所以有4对.
2.如图所示，直线a经过正方形ABCD的顶点A，分别过正方形的顶点B，D作BF⊥a于点F，DE⊥a于点E，若DE=8，BF=5，则EF的长为_________.
【解析】因为四边形ABCD是正方形，所以AB=AD，∠ABC=∠BAD=90°.因为BF⊥a于点F，DE⊥a于点E，所以∠FAB+∠FBA=∠FAB+∠EAD=90°，所以∠FBA=∠EAD.所以在Rt△AFB和Rt△AED中，因为∠AFB=∠DEA=90°，∠FBA=∠EAD ，AB=DA，所以△AFB≌△DEA(AAS)，所以AF=DE=8，BF=AE=5，所以EF=AF+AE=8+5=13.答案：13
3.如图①，A，B，C，D在同一直线上，AB＝CD，DE∥AF，且DE＝AF，试说明：△AFC≌△DEB.如果将BD沿着AD边的方向平行移动，如图②，③时，其余条件不变，结论是否成立？如果成立，请予以说明；如果不成立，请说明理由．