




人教版中考数学第一轮考点过关:第七单元图形的变化课时28图形的对称、平移与旋转
展开课时28 图形的对称、平移与旋转
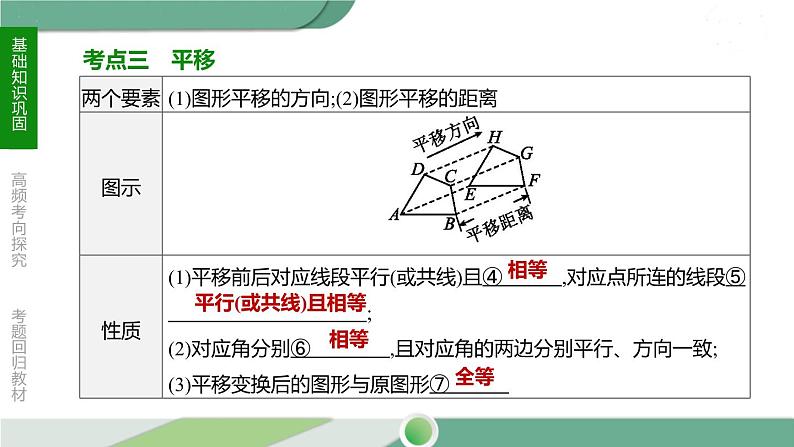
平移 轴对称 中心对称 旋转
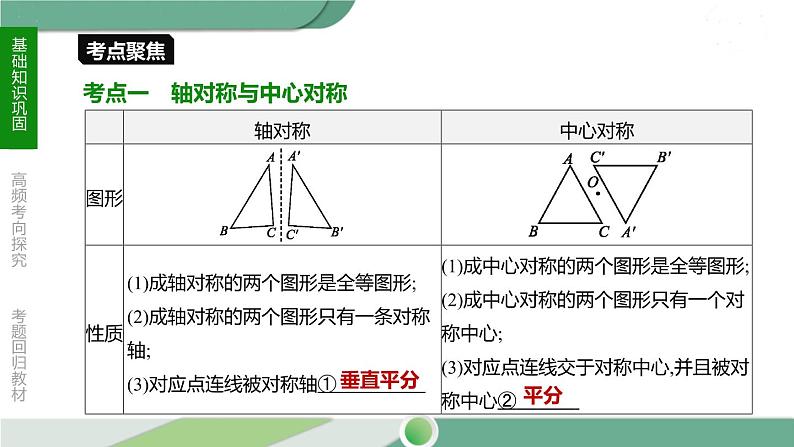
考点一 轴对称与中心对称
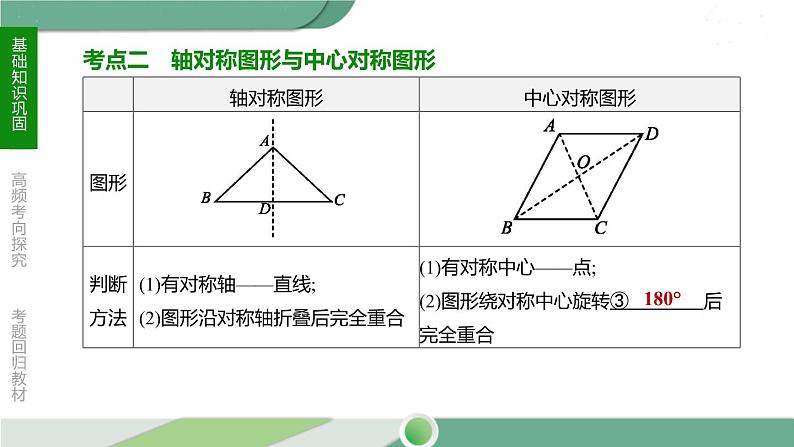
考点二 轴对称图形与中心对称图形
【温馨提示】常见的轴对称图形、中心对称图形
1.[2019·贺州]下列图形中,既是轴对称图形又是中心对称图形的是( )A.正三角形B.平行四边形C.正五边形D.圆
2.如图28-1,将Rt△ABC绕直角顶点C顺时针旋转90°,得到△A'B'C,连接AA',若∠1=25°,则∠BAA'的度数是( )A.55°B.60°C.65°D.70°
[解析]根据旋转的性质可得AC=A'C,因此△ACA'是等腰直角三角形,所以∠CAA'=45°.根据三角形的内角和定理得∠BAC=∠B'A'C=180°-90°-45°-25°=20°.所以∠BAA'=45°+20°=65°.
3.如图28-2,以正方形ABCD的中心为原点建立平面直角坐标系,点A的坐标为(1,1),则点B,C,D的坐标分别为 , , .
4.已知点A的坐标为(-1,3),将点A绕坐标原点O顺时针旋转90°,则点A的对应点A'的坐标为 .
5.△ABC是等边三角形,点O是三条高的交点.若△ABC以点O为旋转中心旋转后能与原来的图形重合,则△ABC旋转的最小角度是 .
[解析]因为△ABC是等边三角形,点O是三条高的交点,所以点O也是三条边的垂直平分线的交点,即点O是△ABC的外心,因此∠AOB=∠BOC=∠COA=120°,旋转的最小角度是120°.
【失分点】 不明白折叠的实质是轴对称导致错误;不能利用轴对称解决最短路线问题.
6.如图28-3,将矩形ABCD沿对角线BD折叠,点C落在点E处,BE交AD于点F,已知∠BDC=62°,则∠DFE的度数为( )A.31°B.28°C.56°D.62°
考向一 轴对称图形和中心对称图形的识别
例1 下列图案中,既是中心对称图形又是轴对称图形的有( )A.1个B.2个C.3个D.4个
[解析]根据轴对称图形与中心对称图形的概念对各图形分析判断后求解.第一个图形既是轴对称图形,又是中心对称图形;第二个图形是轴对称图形,不是中心对称图形;第三个图形是中心对称图形,不是轴对称图形;第四个图形既是轴对称图形,又是中心对称图形.综上所述,既是轴对称图形又是中心对称图形的是第一个和第四个图形,共2个.故选B.
【方法点析】识别轴对称图形的关键是寻找对称轴,图形两部分沿对称轴折叠后可重合;识别中心对称图形的关键是要寻找对称中心,图形绕对称中心旋转180 °后与原图重合.
精练1[2018·柳州]下列图形中,是中心对称图形的是( )
精练2[2019·柳州]下列四个标志是关于安全警示的标志,在这些标志中,是轴对称图形的是( )
精练3[2019·北京]下列倡导节约的图案中,是轴对称图形的是( )
考向二 利用图形变换知识作图
例2 如图28-9,在平面直角坐标系中,把点P(-5,3)向右平移8个单位长度得到点P1,再将点P1绕原点旋转90°得到点P2,则点P2的坐标是 .
(3,-3)或(-3,3)
[解析]首先利用平移的性质得出点P1的坐标,再利用旋转的性质得出符合题意的答案.∵把点P(-5,3)向右平移8个单位长度得到点P1,∴点P1的坐标为(3,3),如图所示,将点P1绕原点逆时针旋转90°得到点P2,则其坐标为(-3,3),将点P1绕原点顺时针旋转90°得到点P2',则其坐标为(3,-3),故符合题意的点P2的坐标为(3,-3)或(-3,3).
精练[2019·龙东地区]如图28-10,正方形网格中,每个小正方形的边长都是一个单位长度,在平面直角坐标系中,△OAB的三个顶点O(0,0),A(4,1),B(4,4)均在格点上.(1)画出△OAB关于y轴对称的△OA1B1,并写出点A1的坐标;(2)画出△OAB绕原点O顺时针旋转90°后得到的△OA2B2,并写出点A2的坐标;(3)在(2)的条件下,求线段OA在旋转过程中扫过的面积.(结果保留π)
解:(1)如图,A1(-4,1).
精练[2019·龙东地区]如图28-10,正方形网格中,每个小正方形的边长都是一个单位长度,在平面直角坐标系中,△OAB的三个顶点O(0,0),A(4,1),B(4,4)均在格点上.(2)画出△OAB绕原点O顺时针旋转90°后得到的△OA2B2,并写出点A2的坐标;
(2)如图,A2(1,-4).
精练[2019·龙东地区]如图28-10,正方形网格中,每个小正方形的边长都是一个单位长度,在平面直角坐标系中,△OAB的三个顶点O(0,0),A(4,1),B(4,4)均在格点上.(3)在(2)的条件下,求线段OA在旋转过程中扫过的面积.(结果保留π)
精练1[2019·甘肃]如图28-12,在矩形ABCD中,AB=10,AD=6,E为BC上一点,把△CDE沿DE折叠,使点C落在AB边上的F处,则CE的长为 .
解:(1)证明:易证△GFE≌△HEC(ASA),可得EG=CH.
精练2[2017·柳州]如图28-16,把这个“十字星”图绕其中心点O旋转,当至少旋转 后,所得图形与原图形重合.
精练3[2019·贺州]如图28-17,正方形ABCD的边长为4,点E是CD的中点,AF平分∠BAE交BC于点F,将△ADE绕点A顺时针旋转90°得△ABG,则CF的长为 .
教材母题——人教版九上P63T10如图28-18,△ABD,△AEC都是等边三角形.BE与DC有什么数量关系?你能用旋转的性质说明上述关系成立的理由吗?
解:BE=DC.理由:∵△ABD是等边三角形,∴AB=AD,∠BAD=60°.同理AE=AC,∠EAC=60°.∴以点A为旋转中心将△ABE顺时针旋转60°就得到△ADC,∴△ABE≌△ADC,∴BE=DC.
【方法点析】旋转前后的图形全等,所以借此可以在较复杂的图形中发现等量(或全等)关系,或通过旋转割补图形,把分散的已知量聚合起来,便于疏通解题思路,打开解题突破口.
数学中考复习考点研究 第七章 图形的变化 命题点4 轴对称与图形的折叠(必考) PPT课件: 这是一份数学中考复习考点研究 第七章 图形的变化 命题点4 轴对称与图形的折叠(必考) PPT课件,共12页。PPT课件主要包含了要点归纳,对称轴,完全重合,对称点,折叠的性质,垂直平分,轴对称,网格中的对称变换,随堂练习,第2题图等内容,欢迎下载使用。
中考数学:第19课时~图形的对称平移与旋转课件PPT: 这是一份中考数学:第19课时~图形的对称平移与旋转课件PPT,共16页。PPT课件主要包含了完全重合,成轴对称,对称轴,垂直平分线,大小和形状,旋转中心,旋转角,形状和大小,对称或中心对称,对称中心等内容,欢迎下载使用。
人教版中考数学7.第七单元 图形的变化 3.第31课时 图形的对称、平移、旋转与位似 PPT课件+练习: 这是一份人教版中考数学7.第七单元 图形的变化 3.第31课时 图形的对称、平移、旋转与位似 PPT课件+练习,文件包含3第31课时图形的对称平移旋转与位似pptx、3第31课时图形的对称平移旋转与位似doc等2份课件配套教学资源,其中PPT共51页, 欢迎下载使用。












