






人教版中考数学第一轮考点过关:第四单元三角形课时18全等三角形
展开全等三角形的概念 全等三角形的性质 全等三角形的判定
考点一 全等三角形的概念及性质
1.定义:能够完全重合的两个三角形叫做全等三角形.2.性质:(1)全等三角形的对应边① ,对应角② ;(2)全等三角形的周长③ ,面积④ ;(3)全等三角形对应的中线、高线、角平分线、中位线都⑤ .
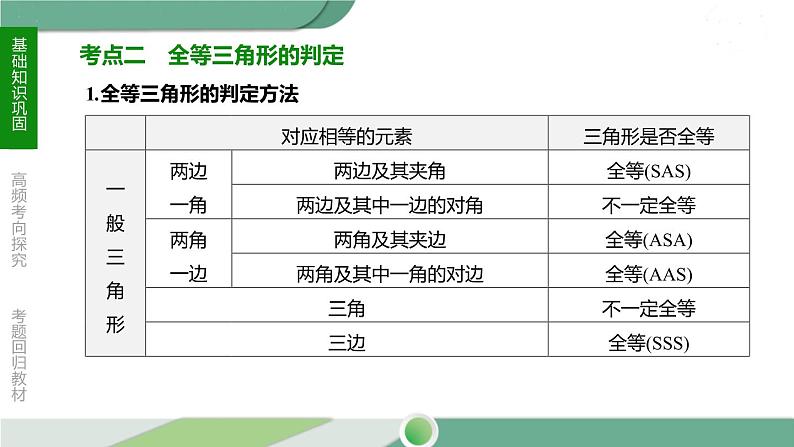
考点二 全等三角形的判定
1.全等三角形的判定方法
1.用直尺和圆规作一个角等于已知角,如图18-1,能得出∠A'O'B'=∠AOB的依据是( )A.SASD.AAS
2.下列说法中,不正确的是( )A.全等三角形的周长相等B.全等三角形的面积相等C.全等三角形一定能够重合D.全等三角形一定关于某条直线对称
[解析]根据全等三角形的定义及性质进行分析判断即可.A.全等三角形的周长相等,正确;B.全等三角形的面积相等,正确;C.全等三角形一定能够重合,正确;D.全等三角形不一定关于某条直线对称,故错误.
3.如图18-2,在△ABC和△DCB中,∠A=∠D=90°,AB=CD,∠ACB=40°,则∠ACD的度数为( )A.10°B.20°C.30°D.40°
4.如图18-3,a,b,c分别表示△ABC的三边长,则图18-4中,与△ABC一定全等的三角形是 ( )
5.根据下列已知条件,能画出唯一△ABC的是( )A.AB=3,BC=4,AC=8B.∠A=60°,∠B=45°,AB=4C.AB=3,BC=2,∠A=30°D.∠C=90°,AB=6
[解析]判断其是否为三角形,即两边之和大于第三边,两边之差小于第三边.另外,由三角形全等的条件可确定三角形的唯一性.A选项中AC与BC两边之差大于第三边,所以A选项不能作出三角形;B选项中两角夹一边,形状固定,所以可作唯一三角形;C选项中∠A并不是AB,BC的夹角,所以不可画出唯一三角形;D选项中两个锐角不确定,可画出多个三角形.
6.小明不慎将一块三角形玻璃摔碎成如图18-5所示的四块,现要到玻璃店配一块与原来一样大小的三角形玻璃,你认为应带去的一块是( )A.第1块 B.第2块C.第3块 D.第4块
[解析]本题应先假定选择哪块,再对应三角形全等判定的条件进行验证.
【失分点】 “SSA”与“SAS”易混淆;忽略判定三角形全等要求至少有一组边相等.
7.如图18-6,已知∠ABC=∠DCB,添加以下条件,不能判定△ABC≌△DCB的是( )A.∠A=∠DB.∠ACB=∠DBCC.AC=DBD.AB=DC
8.下列结论错误的是( )A.全等三角形对应边上的中线相等B.两个直角三角形中,两个锐角对应相等,则这两个三角形全等C.全等三角形对应边上的高相等D.两个直角三角形中,斜边和一个锐角对应相等,则这两个三角形全等
9.如图18-7,△ABC的两条高AD,BE相交于点F,请添加一个条件,使得△ADC≌△BEC(不添加其他字母及辅助线),你添加的条件是 .
答案不唯一,如CA=CB,CE=CD等
考向一 全等三角形的性质
例1 [2018·台湾改编]如图18-8,五边形ABCDE中有一正三角形ACD,若△ABC≌△DEA,且∠E=115°,则∠BAE=( )A.115°B.120°C.125°D.130°
精练1[2015·柳州]如图18-9,△ABC≌△DEF,则EF= .
精练2[2013·柳州]如图18-10,△ABC≌△DEF,请根据图中提供的信息,写出x= .
考向二 全等三角形的判定
例2 如图18-11,OP平分∠MON,PE⊥OM于E,PF⊥ON于F,OA=OB,则图中有 对全等三角形.
[解析] ∵OP平分∠MON,∴∠AOP=∠BOP.∵OA=OB,OP=OP,∴△OAP≌△OBP(SAS).∴AP=BP.∵PE⊥OM,PF⊥ON,∴∠OEP=∠OFP=90°,又∵∠AOP=∠BOP,OP=OP,∴△OEP≌△OFP(AAS).∴PE=PF.∴Rt△AEP≌Rt△BFP(HL).故答案为3.
例3 [2019·山西]已知,如图18-12,点B,D在线段AE上,AD=BE,AC∥EF,∠C=∠F.求证:BC=DF.
精练2[2016·徐州]如图18-14,正方形ABCD的边长为2,点E,F分别在边AD,CD上,∠EBF=45°,则△EDF的周长等于 .
[解析]如图,延长线段DA并截取AG使得AG=CF,连接BG,则可证△BCF≌△BAG,所以BG=BF,因为∠EBF=45°,则可证△GBE≌△FBE,所以EF=GE,由正方形边长为2可求出△EDF的周长=DF+DE+EF=DF+DE+AE+AG=AD+DC=4.
精练3[2018·柳州]如图18-15,AE和BD相交于点C,∠A=∠E,AC=EC.求证:△ABC≌△EDC.
精练4 如图18-16,点D是等边三角形ABC的边AB上一动点,以CD为一边向上作等边三角形EDC,连接AE.(1)求证:△BCD≌△ACE;(2)在点D的运动过程中,你认为∠DAE的大小是否会变化?若变化,说明理由;若不变,求∠DAE的值.
精练4 如图18-16,点D是等边三角形ABC的边AB上一动点,以CD为一边向上作等边三角形EDC,连接AE.(2)在点D的运动过程中,你认为∠DAE的大小是否会变化?若变化,说明理由;若不变,求∠DAE的值.
(2)不发生变化,∠DAE=120°.理由如下:∵△BCD≌△ACE,∴∠DBC=∠EAC=60°,∴∠DAE=∠BAC+∠CAE=120°.
教材母题——人教版八上P56T9如图18-17,∠ACB=90°,AC=BC,AD⊥CE,BE⊥CE,垂足分别为D,E,AD=2.5 cm,DE=1.7 cm.求BE的长.
全等三角形的判定的应用
【方法点析】全等三角形的判定结合全等三角形的性质是证明线段和角相等的重要工具.在判定三角形全等时,关键是选择恰当的判定条件.
精练[2019·桂林]如图18-18,AB=AD,BC=DC,点E在AC上.(1)求证:AC平分∠BAD;(2)求证:BE=DE.
人教版中考数学第一轮考点过关:第八单元统计与概率课时33概率: 这是一份人教版中考数学第一轮考点过关:第八单元统计与概率课时33概率,共39页。PPT课件主要包含了课时33概率,事件的分类,考点一事件的分类,可能性,概率的计算方法,考点三概率的应用,题组一必会题,题组二易错题,图33-1,考向一事件的分类等内容,欢迎下载使用。
人教版中考数学第一轮考点过关:第六单元圆课时25与圆有关的计算: 这是一份人教版中考数学第一轮考点过关:第六单元圆课时25与圆有关的计算,共35页。PPT课件主要包含了考点二圆柱和圆锥,底面圆的周长,πrl,πrl+πr2,题组一必会题,图25-1,图25-2,题组二易错题,图25-3,图25-4等内容,欢迎下载使用。
人教版中考数学第一轮考点过关:第四单元三角形课时20直角三角形与勾股定理: 这是一份人教版中考数学第一轮考点过关:第四单元三角形课时20直角三角形与勾股定理,共47页。PPT课件主要包含了斜边的一半,斜边上的中线,a2+b2c2,图20-1,图20-2,图20-3,题组一必会题,图20-4,图20-5,图20-6等内容,欢迎下载使用。












