






初中北师大版5 三角函数的应用公开课ppt课件
展开知识点一 方向角
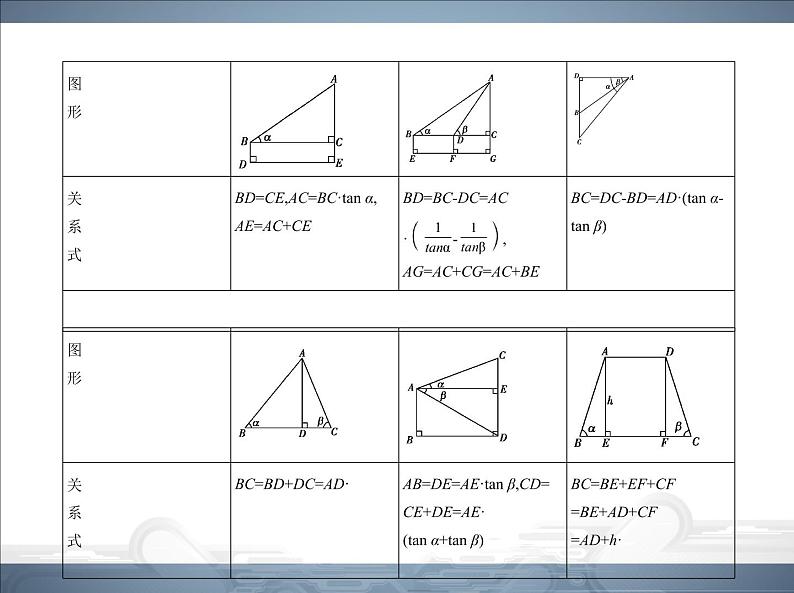
知识点二 三角函数的实际应用 在解决实际问题时,要学会将实际问题转化为数学问题来解决.具体地 说,就是将某些实际问题中的数量关系归结为直角三角形中的边角之间的 关系,这样就可以运用直角三角形的边角关系解决问题.一般有以下几个步骤:(1)根据题意把实际问题转化为数学问题,对于没有给出图形的实际问题, 要弄清题意,并画出示意图.(2)认真分析题意,找出图形中的线段、角所表示的实际意义,并找到所要 解决的问题.(3)根据所要解决的问题找到要求解的直角三角形,有些图形虽然不是直角 三角形,但可通过添加适当的辅助线,把它们分割成一些直角三角形和矩形 (包括正方形).
(4)在解直角三角形时,要选择合适的边角关系式,并借助计算器进行有关 三角函数的计算.(5)所求的结果是边或角时,要按照题目中要求的精确度确定答案,并注明 单位,对于说理型题目(如货轮是否会有触礁的危险),除正确计算结果外,还 要进一步对结果的意义进行说明.常见的图形与关系式如下表所示:
分析 (1)延长PQ交直线AB于点E,根据直角三角形两锐角互余即可求得; (2)设PE=x米,在Rt△APE和Rt△BPE中,根据三角函数用x表示出AE和BE的 长,根据AB=AE-BE即可列出方程求得x的值,再在Rt△BQE中利用三角函数 求得QE的长,则PQ的长度即可求解.
分析 延长AD交BC的延长线于点E,作DF⊥CE于点F.解直角三角形求出 EF,CF,即可解决问题.
点拨 将实际问题转化成解直角三角形问题,理解坡度、坡角的定义是解 答此类题目的前提.若条件中含有线段的比或锐角三角函数值,也可以设未 知数,列方程求解.
通过查阅相关资料和实际测量:兰州市一年中,夏至日这一天的正午时刻, 太阳光线DA与遮阳篷CD的夹角∠ADC最大(∠ADC=77.44°);冬至日这一 天的正午时刻,太阳光线DB与遮阳篷CD的夹角∠BDC最小(∠BDC=30.56 °).窗户的高度AB=2 m.问题解决:根据上述方案及数据,求遮阳篷CD的长.(结果精确到0.1 m,参考数据:sin 30.56°≈0.51,cs 30.56°≈0.86,tan 30.56° ≈0.59,sin 77.44°≈0.98,cs 77.44°≈0.22,tan 77.44°≈4.49)
数学九年级下册5 三角函数的应用背景图ppt课件: 这是一份数学九年级下册5 三角函数的应用背景图ppt课件,共14页。PPT课件主要包含了温故知新,考考你,学习目标,师生共析,大展身手,中考小帮手等内容,欢迎下载使用。
初中数学5 三角函数的应用教课内容ppt课件: 这是一份初中数学5 三角函数的应用教课内容ppt课件,共20页。PPT课件主要包含了锐角三角函数,活动一,活动二,活动三,活动四,活动五,活动六,课堂小结,解题思路导图等内容,欢迎下载使用。
初中数学北师大版九年级下册5 三角函数的应用教学ppt课件: 这是一份初中数学北师大版九年级下册5 三角函数的应用教学ppt课件,共17页。PPT课件主要包含了中考考标要求,回顾旧知,锐角三角函数,类型一同侧型,合作探究,类型二两侧型,类型三复合型,巩固建构,请写出方程等内容,欢迎下载使用。













