






数学九年级下册5 三角函数的应用教学课件ppt
展开1.正确理解方位角、仰角和坡角的概念; 2.三角函数在航海、测量、改造工程等方面的应用
与方位角有关的实际问题
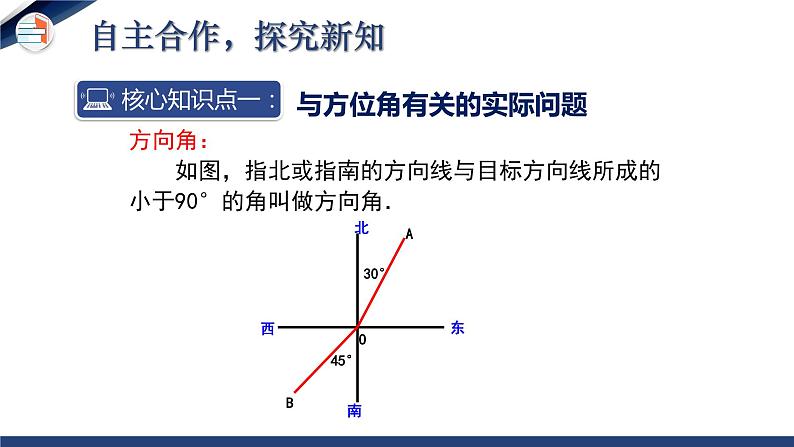
方向角: 如图,指北或指南的方向线与目标方向线所成的小于90°的角叫做方向角.
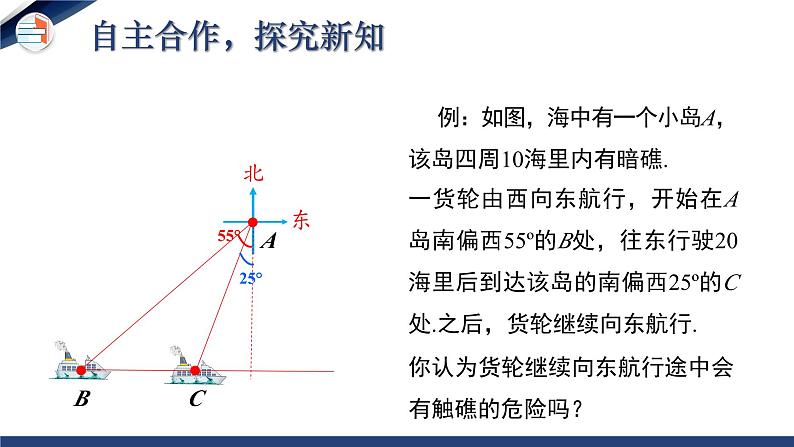
例:如图,海中有一个小岛A,该岛四周10海里内有暗礁.
一货轮由西向东航行,开始在A岛南偏西55º的B处,往东行驶20海里后到达该岛的南偏西25º的C处.之后,货轮继续向东航行.
你认为货轮继续向东航行途中会有触礁的危险吗?
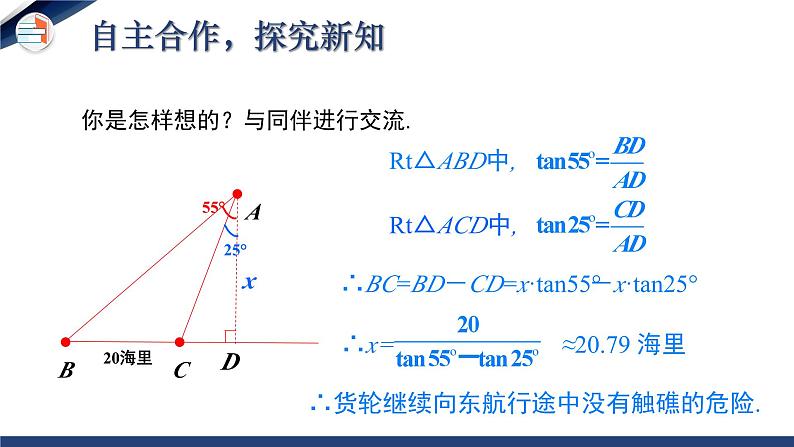
你是怎样想的?与同伴进行交流.
Rt△ABD中,
Rt△ACD中,
∴BC=BD-CD=x·tan55°-x·tan25°
∴x= ≈20.79 海里
∴货轮继续向东航行途中没有触礁的危险.
例:如图, 一艘海轮位于灯塔P的 北偏东65°方向,距离灯塔80 n mile的A处,它沿正南方向航行一段时间后,到达位于灯塔P的南偏东34°方向上的B处.这时,B处距离灯塔 P有多远(结果取整数)?
解:如图,在Rt△APC中, PC =PA • cs(90°-65°) =80 × cs 25° ≈72. 505. 在 Rt△BPC 中, ∠B = 34°, 因此,当海轮到达位于灯塔P的南偏东34°方向时,它距离灯塔P大约 130 n mile.
利用解直角三角形解决简单问题的一般解题步骤: 1. 将实际问题抽象为数学问题;2. 根据条件的特点,适当选用锐角三角函数等去解直角三角形;3. 得到数学问题的答案;4. 得到实际问题的答案.
仰角和俯角: 如图,在视线与水平线所成的角中,视线在水平线上方的叫做_________,视线在水平线下方的叫做________.
例:欣赏完图片后,如图,小明想测量塔CD的高度.他在A处仰望塔顶,测得仰角为30º,再往塔的方向前进50m至B处,测得仰角为60º,那么该塔有多高?(小明的身高忽略不计,结果精确到1m).
答:该塔约有43m高.
解:如图,根据题意可知,∠A=30º, ∠DBC=60º,AB=50m. 设CD=x, 则∠ADC=60º,∠BDC=30º,
例 热气球的探测器显示,从热气球看一栋高楼顶部的仰角为30°,看这栋高楼底部的俯角为60°,热气球与高楼的水平距离为120m,这栋高楼有多高(结果精确到0.1m).
分析:我们知道,在视线与水平线所成的角中视线在水平线上方的是仰角,视线在水平线下方的是俯角,因此,在图中,α=30°,β=60°.Rt△ABD中,α=30°,AD=120,所以利用解直角三角形的知识求出BD;类似地可以求出CD,进而求出BC.
解:如图,α = 30°,β= 60°, AD=120.
答:这栋楼高约为277.1m.
常见的俯角仰角问题的基本图形
坡度和坡角: 如图,通常把坡面的铅直高度h和水平宽度l之比叫_______,用字母i表示,把坡面与水平面的夹角叫做_______,记做α,于是i=____=tanα,显然,坡度越大,α角越大,坡面就越陡.
坡度和坡角有什么区别?
例:某商场准备改善原有楼梯的安全性能,把倾角由原来的40°减至35°,已知原楼梯的长度为4m,调整后的楼梯会加长多少?楼梯多占多长一段地面?(结果精确到0.01m).
如图,∠ADB=90°,
答:调整后的楼梯会加长约0.48m.
答:楼梯多占约0.61m长的一段地面.
例 一段路基的横断面是梯形,高为4米,上底的宽是12米,路基的坡面与地面的倾角分别是45°和30°,求路基下底的宽(精确到0.1米, ).
解:作DE⊥AB,CF⊥AB,垂足分别为E、F.由题意可知 DE=CF=4(米), CD=EF=12(米). 在Rt△ADE中, 在Rt△BCF中,同理可得 因此AB=AE+EF+BF≈4+12+6.93≈22.93(米). 答: 路基下底的宽约为22.93米.
1. 课外活动小组测量学校旗杆的高度. 当太阳光线与 地面成30°角时,测得旗杆在地面上的影长为24米, 那么旗杆的高度约是 ( )
2. 如图,要测量B点到河岸AD的距离,在A点测得 ∠BAD=30°,在C点测得∠BCD=60°,又测得 AC=100米,则B点到河岸AD的距离为 ( )
A. 100米 B. 米 C. 米 D. 50米
3.如图1,在高出海平面100米的悬崖顶A处,观测海平面上一艘小船B,并测得它的俯角为45°,则船与观测者之间的水平距离BC=_________米.4.如图2,两建筑物AB和CD的水平距离为30米,从A点测得D点的俯角为30°,测得C点的俯角为60°,则建筑物CD的高为_____米.
4. 某海滨浴场东西走向的海岸线可近似看作直线l(如图).救生员甲在A处的瞭望台上观察海面情况,发现其正北方向的B处有人发出求救信号.他立即沿AB方向径直前往救援,同时通知正在海岸线上巡逻的救生员乙.乙马上从C处入海,径直向B处游去.甲在乙入海10秒后赶到海岸线上的D处,再向B处游去.若CD=40米,B在C的北偏东35°方向,甲、乙的游泳速度都是2米/秒,则谁先到达B处?请说明理由 (参考数据:sin55°≈0.82,cs55°≈0.57,tan55°≈1.43).
分析: 在Rt△CDB中,利用三角函数即可求得BC,BD的长,则可求得甲、乙所用的时间,比较二者之间的大小即可.
5.如图,某拦河坝截面的原设计方案为:AH∥BC,坡角∠ABC=74°,坝顶到坝脚的距离AB=6 m.为了提高拦河坝的安全性,现将坡角改为55°,由此,点A需向右平移至点D,请你计算AD的长(精确到0.1 m).
分析: 将坝顶与坝脚的距离看做直角三角形的斜边,将坡角看做直角三角形的一个锐角,分别作AE,DF垂直于BC,构造直角三角形,求出BE,BF,进而得到AD的长.
解直角三角形的简单应用
1. 将实际问题抽象为数学问题
2. 根据条件的特点,适当选用锐角三角函数等去解直角三角形
3. 得到数学问题的答案
4. 得到实际问题的答案
1、教材“习题1.6”中第1、2题.2、完成练习册中本课时的练习
初中数学北师大版九年级下册第一章 直角三角形的边角关系5 三角函数的应用授课ppt课件: 这是一份初中数学北师大版九年级下册第一章 直角三角形的边角关系5 三角函数的应用授课ppt课件,共18页。PPT课件主要包含了引入新课,探究新知,巩固练习,达标检测,小结与反思,布置作业等内容,欢迎下载使用。
初中数学5 三角函数的应用课文课件ppt: 这是一份初中数学5 三角函数的应用课文课件ppt,文件包含15三角函数的应用pptx、15三角函数的应用第2课时三角函数的应用2doc、15三角函数的应用第1课时三角函数的应用1doc等3份课件配套教学资源,其中PPT共19页, 欢迎下载使用。
初中北师大版第一章 直角三角形的边角关系5 三角函数的应用多媒体教学课件ppt: 这是一份初中北师大版第一章 直角三角形的边角关系5 三角函数的应用多媒体教学课件ppt,共28页。PPT课件主要包含了教学目标,教学重点,教学难点,情景导入,《泰坦尼克号》,获取新知,北偏东30°,南偏西45°,射线OA,射线OE等内容,欢迎下载使用。














