

初中数学第十八章 平行四边形综合与测试单元测试课后复习题
展开(测试时间:90分钟 满分:120分)
一.选择题(共10小题,每题3分,共30分)
1.已知四边形ABCD是平行四边形,则下列各图中∠1与∠2一定不相等的是( )
2.下列命题中正确的是( )
A.有一组邻边相等的四边形是菱形
B.有一个角是直角的平行四边形是矩形
C.对角线垂直的平行四边形是正方形
D.一组对边平行的四边形是平行四边形
3.如图,在平行四边形ABCD中,∠B=80°,AE平分∠BAD交BC于点E,CF∥AE交AE于点F,则∠1=( )
A.40° B.50° C.60° D.80°
4.如图,在中,AD=8,点E,F分别是BD,CD的中点,则EF等于( )
A.2 B.3 C.4 D.5
5.已知一矩形的两边长分别为7cm和12 cm,其中一个内角的平分线分长边为两部分,这两部分的长分别为( ).
A.6cm和6cm B.7cm和5cm C.4cm和8cm D.3cm和9cm
6.在菱形ABCD中,AB=5,对角线AC=6,若过点A作AE⊥BC于E,则AE=( )
A、4 B、5 C、4.8 D、2.4
7.如图,在平行四边形ABCD中,AB=3cm,BC=5cm,对角线AC,BD相交于点O,则OA的取值范围是( )
A.2cm<OA<5cm
B.2cm<OA<8cm
C.1cm<OA<4cm
D.3cm<OA<8cm
8.如图,菱形ABCD中,∠B=60°,AB=4,则以AC为边长的正方形ACEF的周长为 ( )[来源:]
A.14 B.15 C.16 D.17
9.如图所示,将一张边长为8的正方形纸片折叠,使点落在的中点处,点落在点处,折痕为,则线段的长为( )
A.10 B.4 C. D.
10.已知在四边形ABCD中,对角线AC、BD相交于点O,给出下列四个条件:①AD∥BC ②AD=BC ③OA=OC ④OB=OD.从中任选两个条件,能使四边形ABCD为平行四边形的选法有( )
A.2种 B.3种 C.4种 D.5种
二、填空题(共10小题,每题3分,共30分)
11.如图,在四边形ABCD中,对角线AC、BD交于点O,AD∥BC,请添加一个条件: ,使四边形ABCD为平行四边形(不添加任何辅助线).
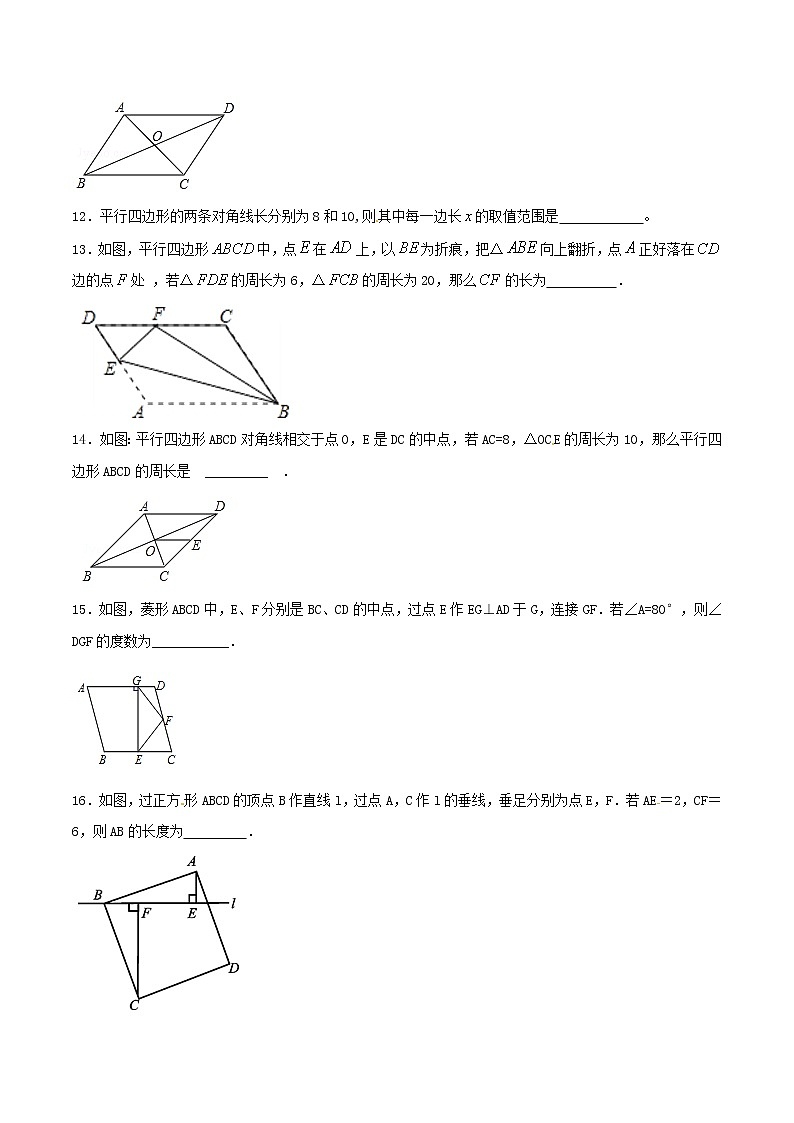
12.平行四边形的两条对角线长分别为8和10,则其中每一边长的取值范围是 。
13.如图,平行四边形中,点在上,以为折痕,把△向上翻折,点正好落在边的点处 ,若△的周长为6,△的周长为20,那么的长为 .
14.如图:平行四边形ABCD对角线相交于点O,E是DC的中点,若AC=8,△OCE的周长为10,那么平行四边形ABCD的周长是 _________ .
15.如图,菱形ABCD中,E、F分别是BC、CD的中点,过点E作EG⊥AD于G,连接GF.若∠A=80°,则∠DGF的度数为___________.
16.如图,过正方形ABCD的顶点B作直线l,过点A,C作l的垂线,垂足分别为点E,F.若AE=2,CF=6,则AB的长度为 .
17.如图,将两条宽度都是为2的纸条重叠在一起,使∠ABC=45°,则四边形ABCD的面积为 _________ .
18.如图,点G是正方形ABCD对角线CA的延长线上任意一点,以线段AG为边作一个正方形AEFG,线段EB和GD相交于点H.若AB=,AG=1,则EB= .
19.如图,在边长为4的正方形ABCD中,E是AB边上的一点,且AE=3,点Q为对角线AC上的动点,则△BEQ周长的最小值为 .
20.如图,在正方形ABCD中,边长为2的等边三角形AEF的顶点E、F分别在BC和CD上,下列结论:
①CE=CF;②∠AEB=75°;③BE+DF=EF;④S正方形ABCD=2+
其中正确的序号是______________
三、解答题(共60分)[来源:学+科+网]
21.(5分)如图,在平行四边形ABCD中,AE=CF,求证:AF=CE.
22.(8分)如图,E,F是四边形ABCD对角线AC上的两点,AD∥BC ,DF∥BE ,AE=CF.
求证:(1)△AFD≌△CEB;
(2)四边形ABCD是平行四边形.
23.(6分)如图,点E、F、G、H分别为矩形ABCD四条边的中点,证明:四边形EFGH是菱形.
24.(8分)如图,四边形ABCD是正方形,BE⊥BF,BE=BF,EF与BC交于点G.
[来源:学。科。网Z。X。X。K]
(1)求证:AE=CF;
(2)若∠ABE=55°,求∠EGC的大小.
25.(8分)如图,E、F分别为△ABC的边BC、CA的中点,延长EF到D,使得DF=EF,连接DA、DB、AE.
(1)求证:四边形ABED是平行四边形;
(2)若AB=AC,试说明四边形AEBD是矩形.
26.(8分)如图,△ABC中,AB=AC,AD是∠BAC的角平分线,点O为AB的中点,连接DO并延长到点E,使OE=OD,连接AE,BE.
(1)求证:四边形AEBD是矩形;
(2)当△ABC满足什么条件时,矩形AEBD是正方形,并说明理由.
27.(8分)如图,E为正方形ABCD对角线BD上的一点,且BE=BC=1.
(1)求∠DCE的度数;
(2)点P在EC上,作PM⊥BD于M,PN⊥BC于N,求PM+PN的值.
28.(9分)37.以△ABC的三边为边在BC的同一侧分别作三个等边三角形,即△ABD、△BCE、△ACF.
(1)请猜想四边形ADEF是什么特殊四边形?并说明理由.
(2)当△ABC满足条件___________时,四边形ADEF为矩形;
(3) 当△ABC满足条件___________时,四边形ADEF不存在.
(测试时间:90分钟 满分:120分)
一.选择题(共10小题,每题3分,共30分)
1.已知四边形ABCD是平行四边形,则下列各图中∠1与∠2一定不相等的是( )
【答案】C.[来源:学*科*网Z*X*X*K]
【解析】
考点:平行四边形的性质.
2.下列命题中正确的是( )
A.有一组邻边相等的四边形是菱形
B.有一个角是直角的平行四边形是矩形
C.对角线垂直的平行四边形是正方形
D.一组对边平行的四边形是平行四边形
【答案】B.
【解析】
试题分析:A、一组邻边相等的平行四边形是菱形,故错误;B、正确;C、对角线垂直的平行四边形是菱形,故错误;D、两组对边平行的四边形才是平行四边形,故错误.
故选B.
考点:命题与定理.
3.如图,在平行四边形ABCD中,∠B=80°,AE平分∠BAD交BC于点E,CF∥AE交AE于点F,则∠1=( )
A.40° B.50° C.60° D.80°
【答案】B.
【解析】
考点:平行四边形的性质.
4.如图,在中,AD=8,点E,F分别是BD,CD的中点,则EF等于( )
A.2 B.3 C.4 D.5
【答案】C.
【解析】
试题分析:∵四边形ABCD是平行四边形,∴BC=AD=8,∵点E、F分别是BD、CD的中点,∴EF=BC=×8=4.
故选C.
考点:1.三角形中位线定理;2.平行四边形的性质.
5.已知一矩形的两边长分别为7cm和12 cm,其中一个内角的平分线分长边为两部分,这两部分的长分别为( ).
A.6cm和6cm B.7cm和5cm C.4cm和8cm D.3cm和9cm
【答案】B
【解析】
试题分析:在矩形ABCD中,AB=7 cm,AD=12 cm,BE是∠ABC的平分线,则∠ABE=∠EBC.由AE∥BC得∠EBC=∠AEB,所以∠ABE=∠AEB,即AE=AB,所以AE=AB=10 cm,ED=12-7=5(cm),
故选B.
考点:矩形的性质
6.在菱形ABCD中,AB=5,对角线AC=6,若过点A作AE⊥BC于E,则AE=( )
A、4 B、5 C、4.8 D、2.4
【答案】C.
【解析】
考点:菱形的性质.
7.如图,在平行四边形ABCD中,AB=3cm,BC=5cm,对角线AC,BD相交于点O,则OA的取值范围是( )
A.2cm<OA<5cm
B.2cm<OA<8cm
C.1cm<OA<4cm
D.3cm<OA<8cm
【答案】C
【解析】
试题分析:∵平行四边形ABCD中,AB=3cm,BC=5cm,∴OA=OC=AC,2cm<AC<8cm,∴1cm<OA<4cm.
故选C.
考点:平行四边形的性质与三角形三边关系.
8.如图,菱形ABCD中,∠B=60°,AB=4,则以AC为边长的正方形ACEF的周长为 ( )
A.14 B.15 C.16 D.17
【答案】C.
【解析】
考点:1.菱形的性质;2.等边三角形的判定与性质;3.正方形的性质.
9.如图所示,将一张边长为8的正方形纸片折叠,使点落在的中点处,点落在点处,折痕为,则线段的长为( )
A.10 B.4 C. D.
【答案】B
【解析】
试题分析:如图,连接ME,作MP⊥CD交CD于点P,
考点:1、翻折变换(折叠问题);2、勾股定理.
10.已知在四边形ABCD中,对角线AC、BD相交于点O,给出下列四个条件:①AD∥BC ②AD=BC ③OA=OC ④OB=OD.从中任选两个条件,能使四边形ABCD为平行四边形的选法有( )
A.2种 B.3种 C.4种 D.5种
【答案】C
【解析】
试题分析:(1)∵①AD∥BC ②AD=BC
∴四边形ABCD为平行四边形(一组对边平行且相等的四边形是平行四边形)
(2)∵③OA=OC ④OB=OD
∴四边形ABCD为平行四边形(对角线互相平分的四边形是平行四边形)
(3)①AD∥BC ③OA=OC
∵①AD∥BC ,∴∠OAD=∠OCB,∠ODA=∠OBC
∵③OA=OC,∴△OAD≌△OCB,∴AD=BC
∴四边形ABCD为平行四边形(一组对边平行且相等的四边形是平行四边形)
(4)①AD∥BC ④OB=OD
∵①AD∥BC ,∴∠OAD=∠OCB,∠ODA=∠OBC
∵④OB=OD,∴△OAD≌△OCB,∴AD=BC
∴四边形ABCD为平行四边形(一组对边平行且相等的四边形是平行四边形)
所以有4种选法,故选C
考点:1、平行四边形的判定;2、全等三角形的判定.
二、填空题(共10小题,每题3分,共30分)
11.如图,在四边形ABCD中,对角线AC、BD交于点O,AD∥BC,请添加一个条件: ,使四边形ABCD为平行四边形(不添加任何辅助线).
【答案】AD=BC(答案不唯一).
【解析】
试题分析:当AD∥BC,AD=BC时,四边形ABCD为平行四边形.
故答案为:AD=BC(答案不唯一).
考点:平行四边形的判定.
12.平行四边形的两条对角线长分别为8和10,则其中每一边长的取值范围是 。
【答案】1<x<9.
【解析】
考点:1.平行四边形的性质;2.三角形三边关系.
13.如图,平行四边形中,点在上,以为折痕,把△向上翻折,点正好落在边的点处 ,若△的周长为6,△的周长为20,那么的长为 .
【答案】7
【解析】
考点:1、翻折变换(折叠问题);2、平行四边形的性质.
14.如图:平行四边形ABCD对角线相交于点O,E是DC的中点,若AC=8,△OCE的周长为10,那么平行四边形ABCD的周长是 _________ .
【答案】24.
【解析】
试题分析:∵平行四边形ABCD对角线相交于点O,E是DC的中点,∴EO是△DBC的中位线,AO=CO,
∵AC=8,∴CO=4,∵△OCE的周长为10,∴EO+CE=10﹣4=6,∴BC+CD=12,∴平行四边形ABCD的周长是24.
考点:1.平行四边形的性质;2.三角形中位线定理.
15.如图,菱形ABCD中,E、F分别是BC、CD的中点,过点E作EG⊥AD于G,连接GF.若∠A=80°,则∠DGF的度数为___________.
【答案】50°.
【解析】
考点:1.菱形的性质;2.全等三角形的判定与性质;3.直角三角形斜边上的中线.
16.如图,过正方形ABCD的顶点B作直线l,过点A,C作l的垂线,垂足分别为点E,F.若AE=2,CF=6,则AB的长度为 .
【答案】2.
【解析】
试题分析:∵四边形ABCD是正方形,∴∠CBF+∠FBA=90°,∠CBF+∠BCF=90°,∴∠BCF=∠ABE,
∵∠AEB=∠BFC=90°,AB=BC,∴△ABE≌△BCF(AAS),∴AE=BF,BE=CF,∴AB=.
考点:1.正方形的性质;2.全等三角形的判定与性质;3.勾股定理.
17.如图,将两条宽度都是为2的纸条重叠在一起,使∠ABC=45°,则四边形ABCD的面积为 _________ .
【答案】4.
【解析】
考点:菱形的判定与性质.
18.如图,点G是正方形ABCD对角线CA的延长线上任意一点,以线段AG为边作一个正方形AEFG,线段EB和GD相交于点H.若AB=,AG=1,则EB= .
【答案】.
【解析】
试题分析:连接BD交AC于O,
考点:1.正方形的性质;2.全等三角形的判定与性质;3.勾股定理.
19.如图,在边长为4的正方形ABCD中,E是AB边上的一点,且AE=3,点Q为对角线AC上的动点,则△BEQ周长的最小值为 .
【答案】6
【解析】
试题分析:连接BD,DE,
∵四边形ABCD是正方形,∴点B与点D关于直线AC对称,∴DE的长即为BQ+QE的最小值,
∵DE=BQ+QE=,∴△BEQ周长的最小值=DE+BE=5+1=6.
考点:1、正方形的性质;2、轴对称的应用
20.如图,在正方形ABCD中,边长为2的等边三角形AEF的顶点E、F分别在BC和CD上,下列结论:[来源:学&科&网]
①CE=CF;②∠AEB=75°;③BE+DF=EF;④S正方形ABCD=2+
其中正确的序号是______________
【答案】①②④.
【解析】
考点:1.正方形的性质;2.全等三角形的判定与性质;3.等边三角形的性质.
三、解答题(共60分)
21.(5分)如图,在平行四边形ABCD中,AE=CF,求证:AF=CE.
【答案】证明见解析.
【解析】
试题分析:由平行四边形的性质证明四边形AECF是平行四边形,即可得到结论.
试题解析:∵四边形ABCD是平行四边形,∴AB∥DC,∴AE∥CF,又∵AE=CF,∴四边形AECF是平行四边形,
∴AF=CE.
考点:平行四边形的判定与性质.
22.(8分)如图,E,F是四边形ABCD对角线AC上的两点,AD∥BC ,DF∥BE ,AE=CF.[来源:ZXXK]
求证:(1)△AFD≌△CEB;
(2)四边形ABCD是平行四边形.
【答案】(1)证明见解析;
(2)证明见解析;[来源:ZXXK]
【解析】
考点:1.平行四边形的判定2.全等三角形的判定与性质.
23.(6分)如图,点E、F、G、H分别为矩形ABCD四条边的中点,证明:四边形EFGH是菱形.[来源:Z*xx*k.Cm]
【答案】证明见解析.
【解析】
考点:1.菱形的判定2.三角形中位线定理3.矩形的性质.
24.(8分)如图,四边形ABCD是正方形,BE⊥BF,BE=BF,EF与BC交于点G.
(1)求证:AE=CF;
(2)若∠ABE=55°,求∠EGC的大小.
【答案】(1)证明见解析;
(2)∠EGC=80°.
【解析】
试题分析:(1)要证AE=CF,若我们能够证明其所在的三角形全等即可.AE位于△AEB中,CF位于△CFB中,
考点:1.三角形全等的判定定理; 2.正方形的性质;3.角形的外角等于和他不相邻的两个内角之和.
25.(8分)如图,E、F分别为△ABC的边BC、CA的中点,延长EF到D,使得DF=EF,连接DA、DB、AE.
(1)求证:四边形ABED是平行四边形;
(2)若AB=AC,试说明四边形AEBD是矩形.
【答案】(1)证明见解析;
(2)证明见解析.
【解析】
试题分析:(1)由已知可得:EF是△ABC的中位线,则可得EF∥AB,EF=AB,又由DF=EF,易得AB=DE,根据有一组对边平行且相等的四边形是平行四边形,即可证得四边形ABED是平行四边形;
(2)由(1)可得四边形AECD是平行四边形,又由AB=AC,AB=DE,易得AC=DE,根据对角线相等的平行四边形是矩形,可得四边形AECD是矩形.
试题解析:(1)∵E、F分别为△ABC的边BC、CA的中点,∴EF∥AB,EF=AB,∵DF=EF,∴EF=DE,∴AB=DE,∴四边形ABED是平行四边形;
(2)∵DF=EF,AF=CF,∴四边形AECD是平行四边形,∵AB=AC,AB=DE,∴AC=DE,∴四边形AECD是矩形.
考点:1.矩形的判定2.平行四边形的判定.
26.(8分)如图,△ABC中,AB=AC,AD是∠BAC的角平分线,点O为AB的中点,连接DO并延长到点E,使OE=OD,连接AE,BE.
(1)求证:四边形AEBD是矩形;
(2)当△ABC满足什么条件时,矩形AEBD是正方形,并说明理由.
【答案】(1)证明见解析;
(2)当∠BAC=90°时,矩形AEBD是正方形.理由见解析.
【解析】
考点:1.矩形的判定;2.正方形的判定.
27.(8分)如图,E为正方形ABCD对角线BD上的一点,且BE=BC=1.
(1)求∠DCE的度数;
(2)点P在EC上,作PM⊥BD于M,PN⊥BC于N,求PM+PN的值.
【答案】(1)22.5°
(2)
【解析】
考点:1、正方形的性质;2、等腰三角形的性质;3、等积法
28.(9分)37.以△ABC的三边为边在BC的同一侧分别作三个等边三角形,即△ABD、△BCE、△ACF.
(1)请猜想四边形ADEF是什么特殊四边形?并说明理由.
(2)当△ABC满足条件___________时,四边形ADEF为矩形;
(3) 当△ABC满足条件___________时,四边形ADEF不存在.
【答案】(1) 四边形ADEF是平行四边形,证明见解析;
(2)∠BAC=150°;
(3)∠BAC=60°.
【解析】
.
考点:1.矩形的判定2.全等三角形的判定与性质3.等边三角形的性质4.平行四边形的判定.
初中数学人教版八年级下册第二十章 数据的分析综合与测试单元测试巩固练习: 这是一份初中数学人教版八年级下册第二十章 数据的分析综合与测试单元测试巩固练习,共20页。试卷主要包含了选择题等内容,欢迎下载使用。
初中数学人教版八年级下册第二十章 数据的分析综合与测试单元测试练习: 这是一份初中数学人教版八年级下册第二十章 数据的分析综合与测试单元测试练习,共23页。试卷主要包含了下面是甲、乙两人10次射击成绩等内容,欢迎下载使用。
初中数学人教版八年级下册第十八章 平行四边形综合与测试单元测试同步达标检测题: 这是一份初中数学人教版八年级下册第十八章 平行四边形综合与测试单元测试同步达标检测题,共25页。试卷主要包含了选择题,填空题,解答题等内容,欢迎下载使用。













