


数学七年级下册第五章 相交线与平行线5.1 相交线5.1.2 垂线课文内容课件ppt
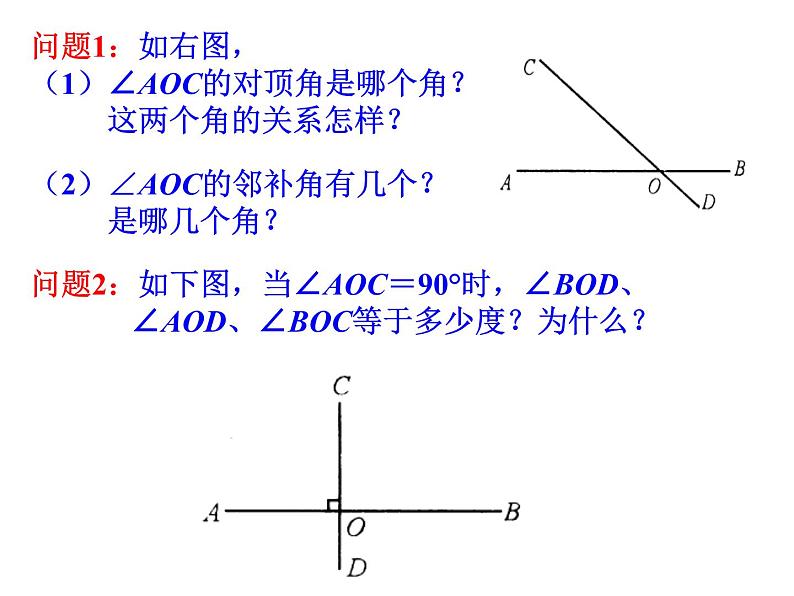
展开问题1:如右图,(1)∠AOC的对顶角是哪个角? 这两个角的关系怎样?
(2)∠AOC的邻补角有几个? 是哪几个角?
问题2:如下图,当∠AOC=90°时,∠BOD、 ∠AOD、∠BOC等于多少度?为什么?
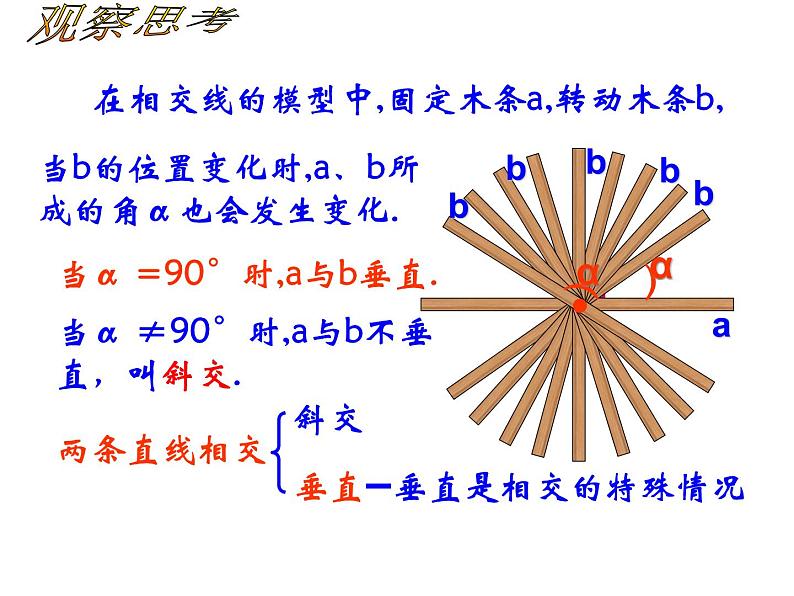
在相交线的模型中,固定木条a,转动木条b,
当α =90°时,a与b垂直.
当b的位置变化时,a、b所成的角α也会发生变化.
当α ≠90°时,a与b不垂直,叫斜交.
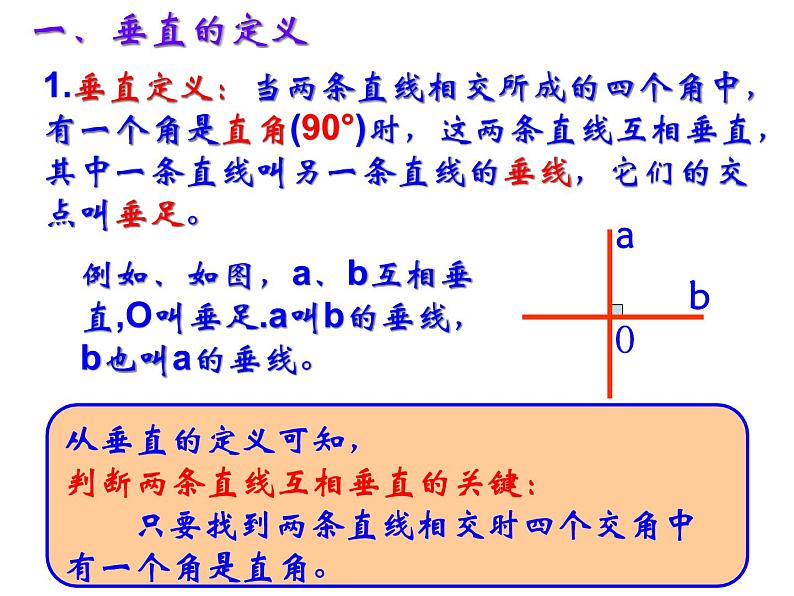
1.垂直定义:当两条直线相交所成的四个角中,有一个角是直角(90°)时,这两条直线互相垂直,其中一条直线叫另一条直线的垂线,它们的交点叫垂足。
例如、如图,a、b互相垂直,O叫垂足.a叫b的垂线,b也叫a的垂线。
从垂直的定义可知,判断两条直线互相垂直的关键: 只要找到两条直线相交时四个交角中有一个角是直角。
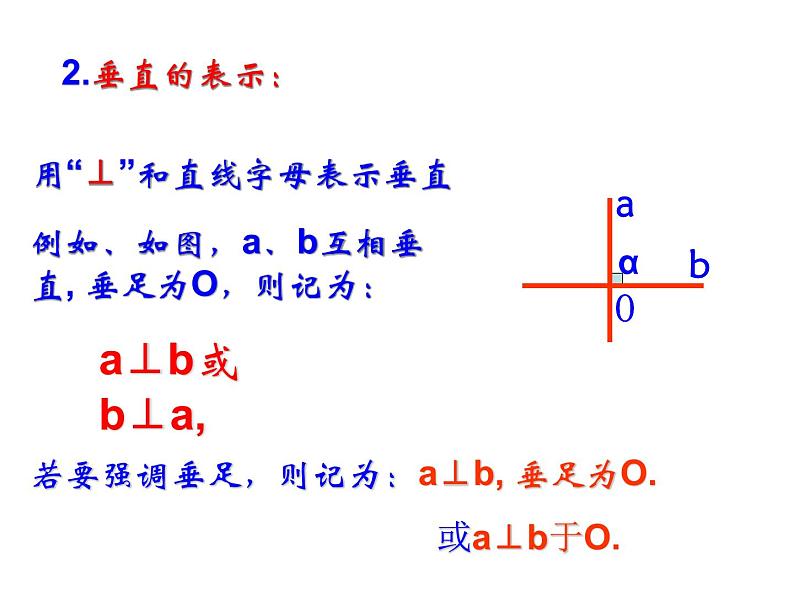
用“⊥”和直线字母表示垂直
例如、如图,a、b互相垂直, 垂足为O,则记为:
若要强调垂足,则记为:a⊥b, 垂足为O.
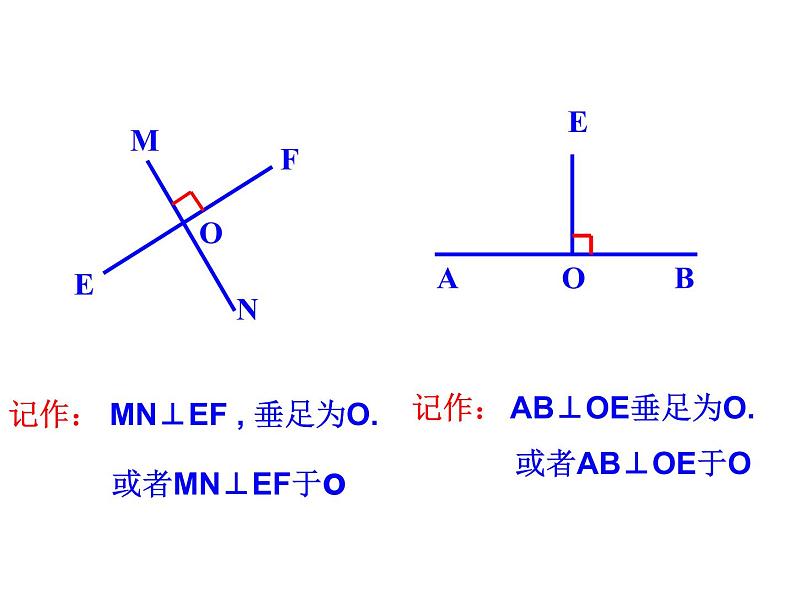
记作: MN⊥EF , 垂足为O. 或者MN⊥EF于
记作: AB⊥OE垂足为O. 或者AB⊥OE于O
∵∠AOC=90°(已知), ∴AB⊥CD(垂直的定义).
如果直线AB、CD 相交于点O,∠AOC=90°(或其它三个角中的一个角等于90°),那么 AB⊥CD.
这个推理过程可以写成:
∵AB⊥CD(已知), ∴∠AOC=90°(垂直的定义).
如果AB⊥CD,那么所得的四个角中,必有一个是直角. 这个推理过程可以写成:
日常生活中,两条直线互相垂直的情形很常见,说出图5.1-6中的一些互相垂直的线条.
你能再举出其他例子吗?
1、下面四种判定两条直线垂直的方法,正确的有 ( )个(1)两条直线相交所成的四个角中有一个角是直角, 则这两条直线互相垂直(2)两条直线相交,只要有一组邻补角相等,则这 两条直线互相垂直(3)两条直线相交,所成的四个角相等,这两条直 线互相垂直(4)两条直线相交,有一组对顶角互补,则这两条 直线互相垂直 (A) 4 (B) 3 (C) 2 (D) 1
例2: 如图AB⊥CD垂足为O,∠COF=56°, 求∠AOE?
解:∵AB⊥CD(已知) ∴∠COB=90°(垂直的定义) ∴∠BOF= ∠COB-∠COF =90°-56°=34° ∴ ∠AOE=∠BOF=34°(对顶角相等) 答:∠AOE=34°.
例3:如图,已知AOB为一直线,∠AOD:∠BOD=3:1,OD平分∠COB,判断AB与OC的位置关系.
1.如图所示,直线AB与CD交于点O,MO⊥AB,垂足为O,ON平分∠AOD.若∠COM=50°,求∠AON的度数.
2.如图,直线AB、CD相交于点O,OE⊥CD于O,OD平分∠BOF,若∠BOE=60°,试求∠AOF的度数
通过本堂课的学习,你掌握了什么内容?收获了哪些?
2:如图:直线AB和 CD相交于点O,OE AB⊥ OE ,OF⊥CD,∠BOF=40º,求∠DOE和∠AOC的度数
1. 如图,直线AB、CD相交于点O, OE⊥AB, ∠1=125°,求∠COE的度数.
人教版七年级下册5.1.2 垂线优质课课件ppt: 这是一份人教版七年级下册5.1.2 垂线优质课课件ppt,文件包含512垂线第2课时垂线段pptx、512垂线第2课时垂线段导学案doc、512垂线教案doc等3份课件配套教学资源,其中PPT共23页, 欢迎下载使用。
数学5.1.2 垂线精品ppt课件: 这是一份数学5.1.2 垂线精品ppt课件,文件包含512垂线第1课时垂线pptx、512垂线第1课时垂线导学案doc、512垂线教案doc等3份课件配套教学资源,其中PPT共27页, 欢迎下载使用。
初中数学人教版七年级下册第五章 相交线与平行线5.1 相交线5.1.2 垂线教学课件ppt: 这是一份初中数学人教版七年级下册第五章 相交线与平行线5.1 相交线5.1.2 垂线教学课件ppt,共20页。PPT课件主要包含了知识要点,垂直的定义,垂线的画法及性质,交点O叫做垂足,符号语言,贴2靠3画,无数条等内容,欢迎下载使用。













