







广东2020中考数学一轮抢分 4.第四节 正方形 课件
展开第五章 四边形
第四节 正方形
(建议时间: 分钟)
基础过关
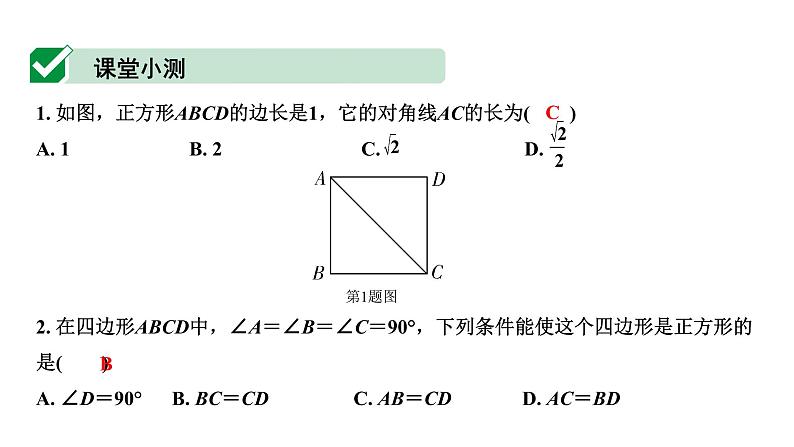
1. (2019毕节)如图,点E在正方形ABCD边AB上,若EB=1,EC=2,那么正方形ABCD的面积为( )
A. B. 3 C. D. 5
第1题图
2. (2019河池)如图,在正方形ABCD中,点E,F分别在BC,CD上,BE=CF,则图中与∠AEB相等的角的个数是( )
A. 1 B. 2 C. 3 D. 4
第2题图
3. 如图,在正方形ABCD中,点E、F分别在CD、BC边上,△AEF是等边三角形,则∠AED=( )
A. 30° B. 45° C. 60° D. 75°
第3题图
- (2018梧州)如图,在正方形ABCD中,A、B、C三点的坐标分别是(-1,2)、(-1,0)、(-3,0),将正方形ABCD向右平移3个单位,则平移后点D的坐标是( )
- (-6,2) B. (0,2) C. (2,0) D. (2,2)
第4题图
- (2019扬州)如图,已知点E在正方形ABCD的边AB上,以BE为边向正方形ABCD外部作正方形BEFG,连接DF,M、N分别是DC、DF的中点,连接MN.若AB=7,BE=5,则MN=________.
第5题图
满分冲关
1. (2019抚顺)如图,AC,BD是四边形ABCD的对角线,点E,F分别是AD,BC的中点,点M,N分别是AC,BD的中点,连接EM,MF,FN,NE,要使四边形EMFN为正方形,则需添加的条件是( )
A. AB=CD,AB⊥CD B. AB=CD,AD=BC C. AB=CD,AC⊥BD D. AB=CD,AD∥BC
第1题图
2. (2019攀枝花)如图,在正方形ABCD中,E是BC边上的一点,BE=4,EC=8,将正方形边AB沿AE折叠到AF,延长EF交DC于G.连接AG,现在有如下4个结论:①∠EAG=45°;②FG=FC;③FC∥AG;④S△GFC=14.其中结论正确的个数是( )
A. 1 B. 2 C. 3 D. 4
第2题图
3. (2019菏泽)如图,E,F是正方形ABCD的对角线AC上的两点,AC=8,AE=CF=2,则四边形BEDF的周长是________.
第3题图
核心素养提升
七巧板
- (2019苏州)“七巧板”是我们祖先的一项卓越创造,可以拼出许多有趣的图形,被誉为“东方魔板”.图①是由边长为10 cm的正方形薄板分为7块制作成的“七巧板”,图②是用该“七巧板”拼成的一个“家”的图形,该“七巧板”中7块图形之一的正方形边长为________cm(结果保留根号).
第1题图
参考答案
第四节 正方形
基础过关
1. B 【解析】∵EC=2,EB=1,∠B=90°,利用勾股定理可得BC=,则正方形ABCD的面积为()2=3.
2. C 【解析】∵四边形ABCD是正方形,∴AD∥BC,∴∠DAE=∠AEB.∵BE=CF,∠ABE=∠BCF,AB=BC,∴△ABE≌△BCF,∴∠BFC=∠AEB.∵AB∥CD,∴∠ABF=∠BFC=∠AEB.∴与∠AEB相等的角有3个.
3. D 【解析】∵四边形ABCD是正方形,∴AB=AD,∠B=∠D=90°,∵△AEF是等边三角形,∴AF=AE,∠EAF=60°,∴Rt△ABF≌Rt△ADE(HL),∴∠BAF=∠DAE==15°,∴∠AED=90°-15°=75°.
4. B
5. 【解析】 如解图,连接FC,则MN=CF,在Rt△CFG中,FG=BE=5,CG=5+7=12,∴FC==13,∴MN=.
第5题解图
满分冲关
1. A 【解析】∵点E,N分别是AD,BD的中点,∴EN是△DAB的中位线. ∴EN∥AB,EN=AB,∵F,M分别是BC,AC的中点,∴FM是△CBA的中位线.∴FM∥AB,FM=AB.∴FM∥NE,FM=NE.∴四边形ENFM是平行四边形.要使四边形ENFM是正方形,则需其邻边相等,且互相垂直.同理根据题意可知EM∥CD,且EM=CD,∴当AB=CD时,EN=EM,当AB⊥CD时,EN⊥EM,故A符合条件.
2. B 【解析】由题意可知AD=AB=AF,则Rt△ADG≌Rt△AFG(HL),∴GD=GF,∠DAG=∠GAF,又∵∠FAE=∠EAB,∴∠EAG=∠GAF+∠FAE=(∠BAF+∠FAD)=∠BAD=45°,∴①正确;设GF=x,则GD=GF=x,又∵BE=4,CE=8,∴DC=BC=12,EF=BE=4,∴CG=12-x,EG=4+x,在Rt△ECG中,由勾股定理可得82+(12-x)2=(4+x)2,解得x=6,∴FG=DG=CG=6,又∵∠FGC≠60°,∴△FGC不是等边三角形,∴FG≠FC,∴②错误;如解图,连接DF,∵Rt△ADG≌Rt△AFG,∴FD⊥AG,又∵FG=DG=GC,则△DFC为直角三角形,∴FD⊥CF,∴FC∥AG,∴③正确;由②可知CG=6,∴S△ECG=EC·CG=24,又∵==,∴S△FCG=S△ECG=,∴④错误,故正确结论为①③,共2个.
第2题解图
3. 8 【解析】∵四边形ABCD是正方形,AC是对角线,∴CD=AD,∠DAE=∠DCF=45°,又∵AE=CF, ∴△DAE≌△DCF(SAS), ∴DE=DF,同理可证:DE=BE,BE=BF,∴DF=DE=BE=BF.∴四边形BEDF是菱形,∵AC=8,AO=OD,AE=2,∴OE=2,OD=4,∴DE===2.∴四边形BEDF的周长为4DE=8.
核心素养提升
1. 【解析】如解图,由题意可知正方形ABCD的边长AB=10 cm,∵△AOB是等腰直角三角形,∴AO=BO=5 cm.∵△BEF是等腰直角三角形,∴BE=EF.∵四边形OEFG是正方形,∴OE=EF=BE.∴OE=.
第1题解图








