广东2020中考数学一轮抢分 4.第四节 二次函数的图像及性质 课件

第三章  函  数

第四节 二次函数的图像及性质

（建议时间：     分钟）

基础过关

1. (2019重庆B卷)抛物线y＝－3x2＋6x＋2的对称轴是(　　)

A. 直线x＝2  B. 直线x＝－2  C. 直线x＝1  D. 直线x＝－1

2. (2019荆门)抛物线y＝－x2＋4x－4与坐标轴的交点个数为(　　)

A. 0  B. 1  C. 2  D. 3

3. (2019兰州)已知点A(1，y1)，B(2，y2)在抛物线y＝－(x＋1)2＋2上，则下列结论正确的是(　　)

A. 2>y1>y2  B. 2>y2>y1  C. y1>y2>2  D. y2>y1>2

4. (2019百色)抛物线y＝x2＋6x＋7可由抛物线y＝x2如何平移得到的(　　)

A. 先向左平移3个单位，再向下平移2个单位

B. 先向左平移6个单位，再向上平移7个单位

C. 先向上平移2个单位，再向左平移3个单位

D. 先向右平移3个单位，再向上平移2个单位

5. (2019河南)已知抛物线y＝－x2＋bx＋4经过(－2，n)和(4，n)两点，则n的值为(　　)

A. －2  B. －4  C. 2  D. 4

6. (2019咸宁)已知点A(－1，m)，B(1，m)，C(2，m－n)(n＞0)在同一个函数的图象上，这个函数可能是(　　)

A. y＝x  B. y＝－  C. y＝x2  D. y＝－x2

7. 二次函数y＝x2－ax＋b的图象如图所示，对称轴为直线x＝2，下列结论不正确的是(　　)

A. a＝4  B. 当b＝－6时，顶点的坐标为(2，－10)

C. b＞－5  D. 当x＞3时，y随x的增大而增大

第7题图

8. (2019济宁)将抛物线y＝x2－6x＋5向上平移两个单位长度，再向右平移一个单位长度后，得到的抛物线解析式是(　　)

A. y＝(x－4)2－6  B. y＝(x－1)2－3  C. y＝(x－2)2－2  D. y＝(x－4)2－2

9. (2019成都)如图，二次函数y＝ax2＋bx＋c的图象经过点A(1，0)，B(5，0)，下列说法正确的是(　　)

A. c<0  B. b2－4ac<0

C. a－b＋c<0  D. 图象的对称轴是直线x＝3

第9题图

10. (2019甘肃省卷)将二次函数y＝x2－4x＋5化成y＝a(x－h)2＋k的形式为____________．

11. (2019宜宾)将抛物线y＝2x2的图象，向左平移1个单位，再向下平移2个单位，所得图象的解析式为____________．

12. (2019济宁)如图，抛物线y＝ax2＋c与直线y＝mx＋n交于A(－1，p)，B(3，q)两点，则不等式ax2＋mx＋c>n的解集是________．

第12题图

13. (2019凉山州)当0≤x≤3时，直线y＝a与抛物线y＝(x－1)2－3有交点，则a的取值范围是________．

满分冲关

1. (2019呼和浩特)二次函数y＝ax2与一次函数y＝ax＋a在同一坐标系中的大致图象可能是(　　)

2. (2019佛山模拟)二次函数y＝ax2＋bx＋c的部分图象如图，则下列说法正确的有(　　)

①对称轴是直线x＝－1；②c＝3；③ab＞0；④当x＜1时，y＞0；

⑤方程ax2＋bx＋c＝0的根是x1＝－3和x2＝1

A. 2个  B. 3个

C. 4个  D. 5个

第2题图

3. (2019湖州)已知抛物线y＝2x2－4x＋c与x轴有两个不同的交点．

(1)求c的取值范围；

(2)若抛物线y＝2x2－4x＋c经过点A(2，m)和点B(3，n)，试比较m与n的大小，并说明理由．

4. 如图，抛物线y＝x2＋bx＋c与x轴交于点A，B，与y轴交于点C，且AB＝2，对称轴为直线x＝2.

(1)求该抛物线的表达式；

(2)根据图象，直接写出不等式x2＋bx＋c＞0的解集；

(3)点D为抛物线上一点，点E为对称轴上一点，若以点A、B、D、E为顶点的四边形是菱形，求点D的坐标．

第4题图

核心素养提升

1. (2019福建)若二次函数y＝|a|x2＋bx＋c的图象过不同的五点A(m，n)，B(0，y1)，C(3－m，n)，D(，y2)，E(2，y3)，则y1，y2，y3的大小关系是(　　)

A．y1＜y2＜y3  B．y1＜y3＜y2  C．y3＜y2＜y1  D．y2＜y3＜y1

参考答案

第四节 二次函数的图像及性质

基础过关

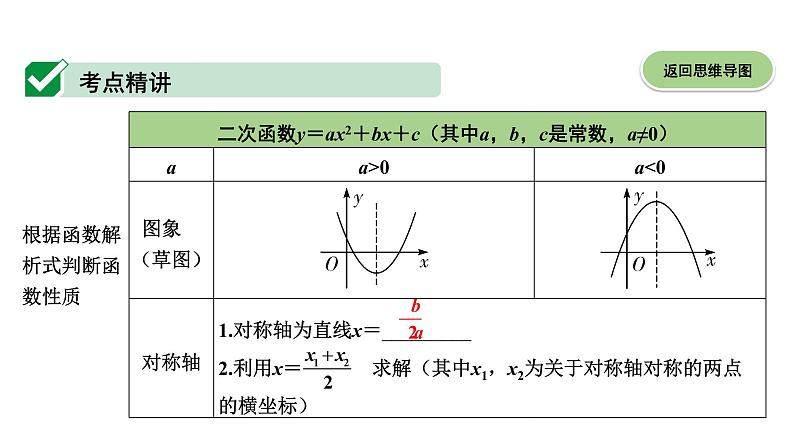
1. C　【解析】∵抛物线y＝－3x2＋6x＋2＝－3(x－1)2＋5，∴抛物线的对称轴为直线x＝1.

2. C　【解析】∵当x＝0时，y＝－4，∴抛物线与y轴的交点为(0，－4)，令y＝0，则－x2＋4x－4＝0，b2－4ac＝16－16＝0，故与x轴只有一个交点，故抛物线与坐标轴的交点个数为2个．

3. A　【解析】∵抛物线开口向下，且对称轴为直线x＝－1，则当x＞－1时，y随x的增大而减小，故y1＞y2，且x＝－1时，y最大＝2.故2＞y1＞y2.

4. A　【解析】抛物线y＝x2＋6x＋7经变形为y＝(x＋3)2－2，故可由抛物线y＝x2先向左平移3个单位，再向下平移2个单位得到．

5. B　【解析】已知抛物线y＝－x2＋bx＋4经过(－2，n)和(4，n)两点，∵两点的纵坐标相同，∴两点关于抛物线的对称轴对称，∴对称轴是直线x＝＝1，∴－＝1，解得b＝2，∴抛物线的解析式为y＝－x2＋2x＋4，当x＝－2时，解得y＝－4.

6. D　【解析】∵A(－1，m)，B(1，m)，∴点A与点B关于y轴对称，∵函数y＝x和y＝－的图象关于原点对称，∴选项A、B错误，∴函数可能是二次函数，对称轴x＝＝0，即y轴．∵n＞0，∴m－n＜m；由B(1，m)，C(2，m－n)可知，在对称轴的右侧，y随x的增大而减小，对于二次函数只有a＜0时，在对称轴的右侧y随x的增大而减小，∴D选项正确．

7. C　【解析】逐项分析如下：

8. D　【解析】∵y＝x2－6x＋5＝(x－3)2－4，∴将抛物线y＝x2－6x＋5向上平移两个单位长度，再向右平移一个单位长度后，得到的抛物线解析式是y＝(x－3－1)2－4＋2＝(x－4)2－2.

9. D　【解析】∵二次函数y＝ax2＋bx＋c的图象与y轴交于正半轴，∴c＞0，故A错误；∵二次函数图象与x轴交于A，B两个不同的点，∴b2－4ac>0，故B错误；∵抛物线与x轴的交点A(1，0)，B(5，0)，∴对称轴为直线x＝＝3，故D正确；∵抛物线开口向上，∴当x＜3时，y随x的增大而减小，∵－1＜1，∴当x＜1时，y＞0，∴当x＝－1时，y＝a－b＋c>0，故C错误．

10. y＝(x－2)2＋1　【解析】配方可得y＝x2－4x＋5＝(x－2)2＋1.

11. y＝2(x＋1)2－2　【解析】根据平移规律“左加右减，上加下减”可知，向左平移1个单位，所得图象的解析为y＝2(x＋1)2，再向下平移2个单位，所得图象的解析式为y＝2(x＋1)2－2.

12. x＜－3或x＞1　【解析】∵抛物线y＝ax2＋c与直线y＝mx＋n交于A(－1，p)，B(3，q)两点，∴－m＋n＝p，3m＋n＝q，∴抛物线y＝ax2＋c与直线y＝－mx＋n交于(1，p)，Q(－3，q)两点．如解图，由ax2＋mx＋c＞n得ax2＋c＞－mx＋n，观察函数图象可知，当x<－3或x>1时，直线y＝－mx＋n在抛物线y＝ax2＋c的下方．∴不等式ax2＋mx＋c>n的解集为x＜－3或x＞1.

第12题解图

13. －3≤a≤1 　【解析】抛物线y＝(x－1)2－3的顶点坐标为(1，－3)，当x＝0时，y＝－2，当x＝3时，y＝1，∴当0≤x≤3时，－3≤y≤1，∴直线y＝a与抛物线有交点时，a的取值范围为－3≤a≤1.

满分冲关

1. D　【解析】当a＞0时，二次函数y＝ax2的图象开口向上，顶点为(0，0)，一次函数y＝ax＋a的图象经过第一、二、三象限且过(－1，0)，故选项B错误，选项D正确；当a＜0时，二次函数y＝ax2的图象开口向下，顶点为(0，0)，一次函数y＝ax＋a的图象经过第二、三、四象限且过(－1，0)，故选项A、C错误．

2. C　【解析】①由二次函数图象得对称轴是直线x＝－1，正确；②根据二次函数与y轴的交点可得c＝3，正确；③由二次函数图象得：开口向下，即a＜0；对称轴－＜0，∴b＜0，ab＞0，正确；④由二次函数图象与x轴的一个交点(1，0)和对称轴直线x＝－1知，该二次函数图象与x轴的另一个交点为(－3，0)，∴x＜－3时，y＜0，错误；⑤∵该二次函数与x轴交点的横坐标为1和－3，∴方程ax2＋bx＋c＝0的根是x1＝－3和x2＝1，正确．

3. 解：(1)b2－4ac＝(－4)2－8c＝16－8c，

由题意，得b2－4ac>0，

∴16－8c>0.

∴c的取值范围是c<2；

(2)m<n.

理由：∵抛物线的对称轴为直线x＝－＝－＝1.a＝2>0，

∴当x≥1时，y随x的增大而增大．

∵2<3，

∴m<n.

4. 解：(1)∵AB＝2，对称轴为直线x＝2.

∴点A的坐标为(1，0)，点B的坐标为(3，0)．

将A、B两点坐标代入解析式，得

解得

∴抛物线的表达式为y＝x2－4x＋3；

(2)x＜1或x＞3；

(3)由(1)可得：y＝x2－4x＋3＝(x－2)2－1，

∴顶点坐标为(2，－1)．

①当AB为菱形的边时，即DE∥AB，当AB＝DE＝2时，D(0，3)或D(4，3)，当D(0，3)时，AD＝＝≠AB，四边形ABED不是菱形；当D(4，3)时，BD＝＝≠AB，四边形ABDE不是菱形．此种情况不存在；

②如解图，当AB为对角线时，根据“菱形ADBE的对角线互相垂直平分，抛物线的对称性”得到点D是抛物线y＝x2－4x＋3的顶点坐标，即(2，－1)时符合题意，故点D的坐标是(2，－1)．

第4题解图

核心素养提升

1. D　【解析】∵抛物线y＝|a|x2＋bx＋c，|a|＞0，∴抛物线的开口向上，∵抛物线图象过A(m，n)，C(3－m，n)，∴对称轴是直线x＝，∵|－|＜|2－|＜|0－|，∴y2＜y3＜y1.