广东2020中考数学一轮抢分 5.第五节 等腰三角形与直角三角形 课件

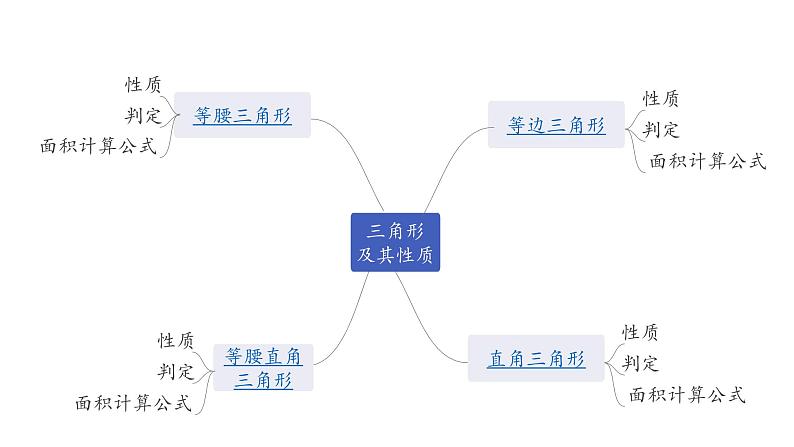
第四章  三角形

第三节 等腰三角形与直角三角形

（建议时间：     分钟）

基础过关

1. (2019抚顺)若一个等腰三角形的两边长分别为2，4，则第三边的长为(　　)

A. 2  B. 3  C. 4  D. 2或4

2. (2019天水)如图，等边△OAB的边长为2，则点B的坐标为(　　)

A. (1，1)  B. (1，)  C. (，1)  D. (，)

第2题图

3. (2019益阳)已知M、N是线段AB上的两点，AM＝MN＝2，NB＝1，以点A为圆心，AN长为半径画弧；再以点B为圆心，BM长为半径画弧，两弧交于点C，连接AC、BC，则△ABC一定是(　　)

A. 锐角三角形  B. 直角三角形  C. 钝角三角形  D. 等腰三角形

4. (2019宁夏)如图，在△ABC中，AC＝BC，点D和E分别在AB和AC上，且AD＝AE.连接DE，过点A的直线GH与DE平行，若∠C＝40°，则∠GAD的度数为(　　)

A. 40°  B. 45°  C. 55°  D. 70°

第4题图

5. 如图，AD，CE分别是△ABC的中线和角平分线．若AB＝AC，∠CAD＝20°，则∠ACE的度数是(　　)

A. 20°  B. 35°  C. 40°  D. 70°

第5题图

6. 如图，等边三角形ABC中，AD⊥BC，垂足为D，点E在线段AD上，∠EBC＝45°，则∠ACE＝(　　)

A. 15°  B. 30°  C. 45°  D. 60° 

第6题图

7. (2019邵阳)如图，在Rt△ABC中，∠BAC＝90°，∠B＝36°，AD是斜边BC上的中线，将△ACD沿AD对折，使点C落在点F处，线段DF与AB相交于点E，则∠BED等于(　　)

A. 120°  B. 108°  C. 72°  D. 36°

第7题图

8. (2018福建)如图，Rt△ABC中，∠ACB＝90°，AB＝6，D是AB的中点，则CD＝________．

第8题图

9. (2019邵阳)公元3世纪初，中国古代数学家赵爽注《周髀算经》时，创造了“赵爽弦图”．如图，设勾a＝6，弦c＝10，则小正方形ABCD的面积是________．

第9题图

10. (2019株洲)如图，在Rt△ABC中，∠ACB＝90°，CM是斜边AB上的中线，E、F分别为MB、BC的中点，若EF＝1，则AB＝________．

第10题图

11. (2019绥化)如图，在△ABC中，AB＝AC，点D在AC上，且BD＝BC＝AD，则∠A＝________度．

第11题图

12.如图，△ABC是等边三角形，延长BC到点D，使CD＝AC，连接AD.若AB＝2，则AD的长为________．

第12题图

13.(2019宜宾)如图，已知直角△ABC中，CD是斜边AB上的高，AC＝4，BC＝3，则AD＝________．

第13题图

满分冲关

1. (2019贵州三州联考)三角板是我们学习数学的好帮手．将一对直角三角板如图放置，点C在FD的延长线上，点B在ED上，AB∥CF，∠F＝∠ACB＝90°，∠E＝45°，∠A＝60°，AC＝10，则CD的长度是________．

第1题图

2. (2019甘肃省卷)定义：等腰三角形的顶角与其一个底角的度数的比值k称为这个等腰三角形的“特征值”．若等腰△ABC中，∠A＝80°，则它的特征值k＝________．

3. (2019哈尔滨)在△ABC中，∠A＝50°，∠B＝30°，点D在AB边上，连接CD，若△ACD为直角三角形，则∠BCD的度数为__________度．

4. (2019重庆A卷 )如图，在△ABC中，AB＝AC，D是BC边上的中点，连接AD，BE平分∠ABC交AC于点E，过点E作EF∥BC交AB于点F.

(1)若∠C＝36°，求∠BAD的度数；

(2)求证：FB＝FE.

第4题图

核心素养提升

《数书九章》——沙田几何

1. (2018长沙)我国南宋著名数学家秦九韶的著作《数书九章》里记载有这样一道题目：“问有沙田一块，有三斜，其中小斜五里，中斜十二里，大斜十三里，欲知为田几何？”这道题讲的是：有一块三角形沙田，三条边长分别为5里，12里，13里，问这块沙田面积有多大？题中的“里”是我国市制长度单位，1里＝500米，则该沙田的面积为(　　)

A. 7.5平方千米  B. 15平方千米  C. 75平方千米  D. 750平方千米

2. (2019衢州)“三等分角”大约是在公元前五世纪由古希腊人提出来的，借助如图所示的“三等分角仪”能三等分任一角，这个三等分角仪由两根有槽的棒OA，OB组成，两根棒在O点相连并可绕O转动，C点固定，OC＝CD＝DE，点D，E可在槽中滑动，若∠BDE＝75°，则∠CDE的度数是(　　)

A. 60°  B. 65°  C. 75°  D. 80°

第2题图

3. 如图①是一把园林剪刀，把它抽象为图②，其中OA＝OB，若剪刀张开的角为30°，则∠A＝________度．

第3题图

参考答案

第三节 等腰三角形与直角三角形

基础过关

1. C　【解析】当2是这个等腰三角形的腰时，其三边长为2，2，4，∵2＋2＝4，此时不能构成三角形，不合题意；当4为这个等腰三角形的腰时，其三边长为2，4，4，可以构成三角形，则第三边的长为4.

2. B　【解析】如解图，过点B作BD⊥OA于点D，∵△OAB为等边三角形，边长为2，∴∠BOA＝60°，OA＝OB＝2.∴OD＝1，BD＝＝＝.∴点B的坐标为(1，)．

第2题解图

3. B　【解析】如解图，∵AM＝MN＝2，NB＝1，∴AB＝AM＋MN＋NB＝2＋2＋1＝5.∵由作法知：AC＝AN＝4，BC＝BM＝3，∴BC2＋AC2＝32＋42＝52＝AB2，∴△ABC一定是直角三角形．

第3题解图

4. C　【解析】∵AC＝BC，∠C＝40°，∴∠BAC＝∠B＝×(180°－40°)＝70°，∵AD＝AE，∴∠ADE＝∠AED＝×(180°－70°)＝55°，∵GH∥DE，∴∠GAD＝∠ADE＝55°.

5. B　【解析】∵AB＝AC，且AD是底边BC的中线，∴AD⊥BC，即∠ADC＝90°，∴∠ACD＝90°－∠CAD＝70°，又∵CE平分∠ACB，∴∠ACE＝∠ACD＝35°.

6. A　【解析】∵△ABC为等边三角形，AD⊥BC，∴BD＝DC，∠ACB＝60°，∴AD垂直平分线段BC，∴BE＝CE，∴∠EBC＝∠ECB＝45°，∴∠ACE＝∠ACB－∠ECB＝60°－45°＝15°.

7. B　【解析】∵AD为Rt△ABC斜边BC上的中线，∴AD＝CD＝DB＝DF，∵∠B＝36°，∴∠C＝90°－36°＝54°，∵AD＝CD，∴∠C＝∠CAD＝54°，∴∠F＝∠DAF＝54°，∴∠ADF＝180°－54°－54°＝72°，∠EAD＝90°－54°＝36°，∴∠BED＝∠EAD＋∠ADF＝36°＋72°＝108°.

8. 3

9. 4　【解析】∵勾a＝6，弦c＝10，∴股b＝＝8，∴AD＝8－6＝2，∴小正方形的面积是2×2＝4.

10. 4　【解析】在Rt△ABC中，∵∠ACB＝90°，CM是斜边AB上的中线，∴AB＝2CM，∵E、F分别为MB，BC的中点，∴EF是△CMB的中位线，又∵EF＝1，∴CM＝2EF＝2，∴AB＝2CM＝4.

11. 36　【解析】由题意可得，∠C＝∠ABC＝2∠A，设∠A＝x，则∠C＝∠ABC＝2x，∴x＋2x＋2x＝180°，解得x＝36°.∴∠A＝36°.

12. 2　 【解析】∵△ABC是等边三角形，∴∠B＝∠BAC＝∠ACB＝60°，∵CD＝AC，∴∠CAD＝∠D，∵∠ACB＝∠CAD＋∠D＝60°，∴∠CAD＝∠D＝30°，∴∠BAD＝∠BAC＋∠CAD＝90°，∴AD＝＝＝2.

13. 　【解析】根据勾股定理可得，AB＝＝＝5，∵S△ABC＝×3×4＝6，∴S△ABC＝AB·CD＝×5×CD＝CD＝6，∴CD＝.在Rt△ACD中，AD＝＝＝.

满分冲关

1. 15－5　【解析】如解图，过点B作BM⊥FD于点M，在△ACB中，∠ACB＝90°，∠A＝60°，AC＝10，∴∠ABC＝30°，BC＝AC＝10.∵AB∥CF，∴∠BCM＝∠ABC＝30°.∴BM＝×10＝5.CM＝＝＝15.在△EFD中，∠F＝90°，∠E＝45°，∴∠EDF＝45°，∴MD＝BM＝5.∴CD＝CM－MD＝15－5.

第1题解图

2. 或　【解析】当∠A为顶角时，则底角∠B＝∠C＝(180°－∠A)＝50°，此时的特征值k＝＝；当∠A为底角时，则顶角(∠B或∠C)＝180°－2∠A＝20°，此时的特征值k＝＝.综上，k的值为或.

3. 60或10　【解析】分两种情况：①如解图①，当∠ADC＝90°时， ∵∠B＝30°， ∴∠BCD＝90°－30°＝60°；②如解图②，当∠ACD＝90°时，∵∠A＝50°，∠B＝30°， ∴∠ACB＝180°－30°－50°＝100°，∴∠BCD＝100°－90°＝10°，综上，∠BCD的度数为60°或10°.

第3题解图

4. (1)解：∵AB＝AC，

∴∠ABC＝∠C.

又∵D是BC的中点，

∴AD平分∠BAC，即∠BAD＝∠BAC.

∵∠C＝36°，

∴∠BAC＝180°－2∠C＝108°，

∴∠BAD＝∠BAC＝54°；

(2)证明：∵BE平分∠ABC，

∴∠FBE＝∠EBD.

∵EF∥BC，

∴∠FEB＝∠EBD.

∴∠FBE＝∠FEB，

∴FB＝FE.

核心素养提升

1. A　【解析】∵52＋122＝132，∴该沙田为直角三角形沙田，又∵5里＝5×500米＝2500米＝2.5千米，12里＝12×500米＝6000米＝6千米，∴该沙田的面积为×6×2.5＝7.5平方千米．

2. D　【解析】设∠O＝x，∵OC＝CD，∴∠CDO＝∠O＝x，∴∠ECD＝2∠O＝2x，∵CD＝DE，∴∠CED＝∠ECD＝2x，∵∠BDE＝∠O＋∠CED＝75°，∴3x＝75°，解得x＝25°，∴∠ECD＝∠CED＝50°，∴∠CDE＝180°－2∠ECD＝80°.

3. 75　【解析】由题意知∠BOA＝30°，∵OA＝OB，∴∠A＝∠B＝×(180°－30°)＝75°.