








广东2020中考数学一轮抢分 5.第五节 解直角三角形的实际应用 课件
展开第四章 三角形
第七节 解直角三角形的实际应用
(建议时间: 分钟)
基础过关
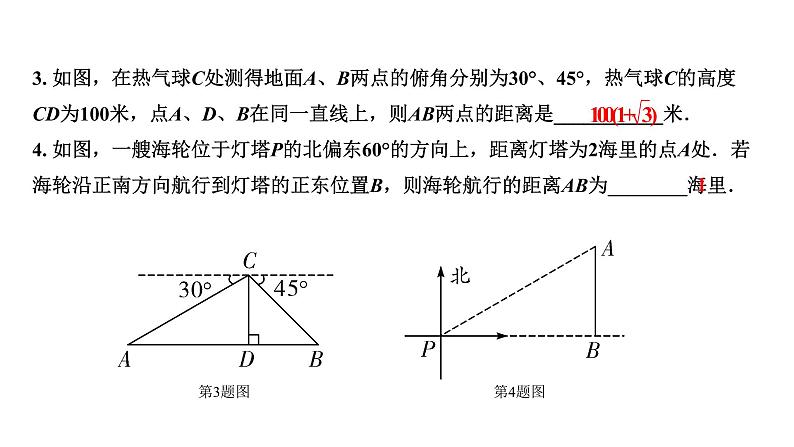
1. (2019河北)如图,从点C观测点D的仰角是( )
A. ∠DAB B. ∠DCE C. ∠DCA D. ∠ADC
第1题图
2. (2019长春)如图,一把梯子靠在垂直于水平地面的墙上,梯子AB的长是3米.若梯子与地面的夹角为α,则梯子顶端到地面的距离BC为( )
A. 3sinα米 B. 3cosα米 C. 米 D. 米
第2题图
- (2019衢州)如图,人字梯AB,AC的长都为2米,当α=50°时,人字梯顶端离地面的高度AD是________米(结果精确到0.1 m,参考数据:sin50°≈0.77,cos50°≈0.64,tan50°≈1.19).
第3题图
- (2019枣庄)如图,小明为了测量校园里旗杆AB的高度,将测角仪CD竖直放在距旗杆底部B点6 m的位置,在D处测得旗杆顶端A的仰角为53°.若测角仪的高度是1.5 m,则旗杆AB的高度约为________m.(精确到0.1 m.参考数据:sin53°≈0.80,cos53°≈0.60,tan53°≈1.33)
第4题图
5. (2019青海)如图是矗立在高速公路边水平地面上的交通警示牌,经过测量得到如下数据:AM=4米,AB=8米,∠MAD=45°,∠MBC=30°.则CD的长为__________米.(结果保留根号)
第5题图
6.(2019宁波)如图,某海防哨所O发现在它的西北方向,距离哨所400米的A处有一艘船向正东方向航行,航行一段时间后到达哨所北偏东60°方向的B处,则此时这艘船与哨所的距离OB约为________米.(精确到1米,参考数据:≈1.414,≈1.732)
第6题图
7.(2019辽阳)某数学小组三名同学运用自己所学的知识检测车速,他们将观测点设在一段笔直的公路旁且距公路100米的点A处,如图所示,直线l表示公路,一辆小汽车由公路上的B处向C处匀速行驶,用时5秒,经测量,点B在点A北偏东45°方向上,点C在点A北偏东60°方向上,这段公路最高限速60千米/小时,此车________(填“超速”或“没有超速”).(参考数据:≈1.732)
第7题图
8. (2019台州)图①是一辆在平地上滑行的滑板车,图②是其示意图.已知车杆AB长92 cm,车杆与脚踏板所成的角∠ABC=70°,前后轮子的半径均为6 cm,求把手A离地面的高度(结果保留小数点后一位,参考数据:sin70°≈0.94,cos70°≈0.34,tan70°≈2.75).
第8题图
9. (2019临沂)鲁南高铁临沂段修建过程中需要经过一座小山.如图,施工方计划沿AC方向开挖隧道,为加快施工进度,要在小山的另一侧D(A,C,D共线)处同时施工.测得∠CAB=30°,AB=4 km,∠ABD=105°,求BD的长.
第9题图
10. (2019黄冈)如图,两座建筑物的水平距离BC为40 m,从A点测得D点的俯角α为45°,测得C点的俯角β为60°.求这两座建筑物AB,CD的高度.(结果保留小数点后一位,≈1.414,≈1.732)
第10题图
满分冲关
1. (2019河南)数学兴趣小组到黄河风景名胜区测量炎帝塑像(塑像中高者)的高度.如图所示,炎帝塑像DE在高55 m的小山EC上,在A处测得塑像底部E的仰角为34°,再沿AC方向前进21 m到达B处,测得塑像顶部D的仰角为60°,求炎帝塑像DE的高度.(精确到1 m.参考数据:sin34°≈0.56,cos34°≈0.83,tan34°≈0.67,≈1.73)
第1题图
2. (2019青岛)如图,某旅游景区为方便游客,修建了一条东西走向的木栈道AB,栈道AB与景区道路CD平行.在C处测得栈道一端A位于北偏西42°方向,在D处测得栈道另一端B位于北偏西32°方向.已知CD=120 m,BD=80 m,求木栈道AB的长度(结果保留整数).
(参考数据:sin32°≈,cos32°≈,tan32°≈,sin42°≈,cos42°≈,tan42°≈)
第2题图
参考答案
第七节 解直角三角形的实际应用
基础过关
1. B 【解析】视线与水平线所成的角叫做仰角,即从点C观测点D的仰角为∠DCE.
2. A 【解析】由题知α对应的角为∠BAC,则sinα=,已知AB=3米,则BC=AB·sinα=3sinα米.
3. 1.5 【解析】在Rt△ACD中,AD=AC·sinα=2sin50°≈2×0.77=1.54≈1.5米.
4. 9.5 【解析】如解图,过点D作DE⊥AB于点E,∵在D处测得旗杆顶端A的仰角为53°,∴∠ADE=53°.∵BC=DE=6 m,∴AE=DE·tan53°≈6×1.33≈7.98 m.∴AB=AE+BE=AE+CD≈7.98+1.5=9.48 m≈9.5 m.
第4题解图
5. 4-4 【解析】在Rt△ADM中,DM=AM=4,在Rt△BCM中,tan∠MBC=,∴=.∴CD=4-4.
6. 566 【解析】如解图, 设AB与正北方向线的交点为C,则AB⊥OC,由题意知在等腰直角△OAC中OA=400,∴OC=200,在Rt△OCB中,∠BOC=60°,∴OB===400≈566(米).
第6题解图
7. 没有超速 【解析】如解图,过点A作AD⊥l于点D.根据题意可知,∠DAB=45°,∠DAC=60°,∴BD=AD,CD=AD,∵AD=100米,∴BC=100-100≈73.2米,用时为5秒,∴速度为=14.64米/秒,∵60千米/小时≈16.67米/秒>14.64米/秒,∴没有超速.
第7题解图
8. 解:如解图,过点A作AD⊥BC于点D,
在Rt△ABD中,∠ABD=70°,
∴sin70°=.
又∵AB=92 cm,
∴AD=AB·sin70°≈92×0.94=86.48cm.
∴把手A离地面的高度为86.48+6=92.48≈92.5cm.
第8题解图
9. 解:如解图,过点B 作BE⊥AD交AD 于点E,
∵∠CAB=30°,∠ABD=105°,
∴∠D=45°.
在Rt△AEB中,BE=AB·sin∠CAB=4×=2 km,
在Rt△DEB中,BD===2 km,
∴BD的长为2 km.
第9题解图
10. 解:如解图,过点D作DE⊥AB于点E,
∵∠α=45°,∠β=60°,
∴∠DAB=45°,∠CAB=30°.
∴△AED为等腰直角三角形,
四边形BCDE为矩形.
∴AE=DE=BC=40 m.
在Rt△ABC中,AB===40≈40×1.732≈69.3 m,
∴CD=BE=AB-AE=40-40≈29.3 m.
∴两座建筑物AB,CD的高度分别为69.3 m,29.3 m.
第10题解图
满分冲关
1. 解:在Rt△ACE中,∵∠A=34°,CE=55,
∴AC=≈≈82.1 m.
∴BC=AC-AB≈82.1-21=61.1 m.
在Rt△BCD中,∵∠CBD=60°,
∴CD=BC·tan60°≈61.1×1.73≈105.7 m.
∴DE=CD-CE≈105.7-55≈51 m.
答:炎帝塑像DE的高度约为51 m.
2. 解:如解图,过点C作CE⊥AB于点E,过点D作DF⊥AB交AB的延长线于点F.
∵AB∥CD,
∴∠ECD=∠BEC=90°.
∴四边形ECDF为矩形.
∴EF=CD=120 m,DF=CE.
在Rt△BDF中,∵BD=80 m,∠BDF=32°,
∴BF=BD·sin32°≈80×=42.5 m,DF=BD·cos32°≈80×=68 m,
∴CE=DF≈68 m.
在Rt△ACE中,∵∠ACE=42°,
∴AE=CE·tan42°≈68×=61.2 m.
∴AB=AE+EB=AE+EF-BF≈138.7 m≈139 m.
答:木栈道AB的长度约为139 m.








