初中冀教版22.6 正方形公开课课件ppt

这是一份初中冀教版22.6 正方形公开课课件ppt，共33页。PPT课件主要包含了课堂讲解，课时流程，逐点导讲练，课堂小结，作业提升，知识点，正方形的定义，AC＝BD，正方形边的性质，正方形角的性质等内容，欢迎下载使用。

正方形的定义正方形边的性质正方形角的性质
鞋匠们钉鞋时常用的铁钉的横截面的形状，不像普通铁钉那样是圆的，而呈正方形，你知道其中的原因吗？
你提的问题十分有趣，为什么是正方形而不是圆形，这是正方形独特的性质所起的作用，我们只要再进一步深入接触正方形就会知道其中的道理.
做一做：用一张长方形的纸片(如图所示)折出一个正方形．
问题：什么样的四边形是正方形？
正方形(square)是我们熟悉的几何图形，它的四条边都相等，四个角都是直角.因此，正方形既是矩形，又是菱形.它既有矩形的性质，又有菱形的性质.
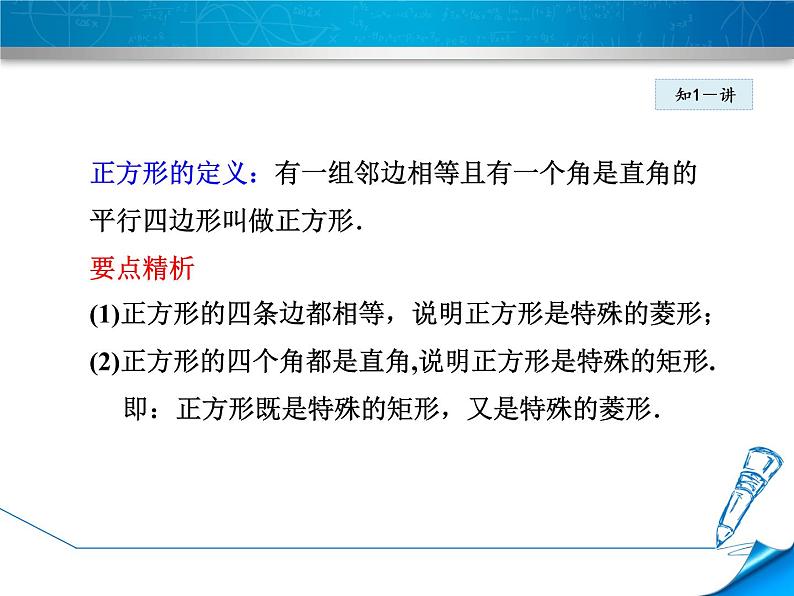
正方形的定义：有一组邻边相等且有一个角是直角的平行四边形叫做正方形．要点精析(1)正方形的四条边都相等，说明正方形是特殊的菱形；(2)正方形的四个角都是直角,说明正方形是特殊的矩形. 即：正方形既是特殊的矩形，又是特殊的菱形．
例1 如图，已知点E是正方形ABCD的边CD上一点，点F是CB的延长线上一点，且EA⊥AF. 求证：DE=BE.
本题要证明两条线段相等，而证明线段相等的方法有很多，根据题中所给的条件，由正方形ABCD，我们可以得到边相等，角相等，也可以得到平行，所以在可以得到比较多的条件的情况下，一般会想到用全等去解决，而本题中全等的条件也很充足，那么问题即可解决．
∵四边形ABCD是正方形，∴AD=AB，∠D=∠ABF=∠BAD=90°．∴∠BAE+∠EAD=90°．∴EA⊥AF，∴∠BAE+∠FAB=90°．∴∠EAD=∠FAB．∴△ABF≌△ADE．∴DE=BF.
知道正方形就说明它的四边都相等，四个角都是直角.
如图，如果正方形ABCD旋转后能与正方形 CFED重合，那么图形所在的平面上可以作为旋 转中心的点共有多少个？请指出它们的位置.
共3个．分别是点D、点C和线段CD的中点．
下面四个定义中不正确的是(　　)A．有一个角是直角的平行四边形叫做矩形B．有一组邻边相等的四边形叫做菱形C．有一组邻边相等，并且有一个角是直角的 平行四边形叫做正方形D．有一组邻边相等的平行四边形叫做菱形
已知在四边形ABCD中，∠A＝∠B＝∠C＝90°，如果添加一个条件，即可推出该四边形是正方形，那么这个条件可以是(　　)A．∠D＝90° B．AB＝CDC．AD＝BC D．BC＝CD
【中考·兰州】▱ABCD的对角线AC与BD相交于点O，且AC⊥BD，请添加一个条件：________，使得▱ABCD为正方形．
正方形的性质：具有矩形、菱形、平行四边形的一切性质，即：①边：四条边相等，邻边垂直，对边平行；②角：四个角都是直角.
例2 已知：如图，在正方形ABCD中，对角线的交 点为O，E是OB上的一点，DG⊥AE于G，DG 交AO于F，求证：EF∥AB.
要证EF∥AB，由于∠OBA＝45°，∠EOF＝90°，即需证∠OEF＝45°，即要证明OE＝OF，而OE＝OF可通过证明△AEO≌△DFO获得．
∵四边形ABCD是正方形，∴∠AOE＝∠DOF＝90°，AO＝DO，∠OBA＝45°.又∵DG⊥AE，∴∠EAO＋∠AEO＝∠EDG＋∠GED＝90°.∵∠AEO＝∠GED，∴∠EAO＝∠EDG＝∠FDO.∴△AEO≌△DFO (ASA)．∴OE＝OF.∴∠OEF＝45°. ∴∠OEF＝∠OBA.∴EF∥AB.
通过证明三角形全等得到边和角相等，再进一步得到平行或垂直，是有关正方形中证边或角相等的最常用的方法，而正方形的四条边相等，四个角都是直角为证明三角形全等提供了条件．
1 已知：如图，四边形ABCD和BGFE都是正方 形.求证：AE=CG.
∵四边形ABCD是正方形，∴AB＝CB，∠ABC＝90°.∵四边形BGFE是正方形，∴BE＝BG，∠EBG＝90°.∴∠ABC－∠EBC＝∠EBG－∠EBC，即∠ABE＝∠CBG.∴△ABE≌△CBG.∴AE＝CG.
正方形具有而矩形不一定具有的性质是(　　)A．四个角都相等 B．四条边相等C．对角线相等 D．对角线互相平分
【中考·宁波】一个大矩形按如图方式分割成九个小矩形，且只有标号为①和②的两个小矩形为正方形，在满足条件的所有分割中，若知道九个小矩形中n个小矩形的周长，就一定能算出这个大矩形的面积，则n的最小值是(　　)A．3 B．4 C．5 D．6
如图，正方形ABCD的面积为1，则以相邻两边中点连线EF为边的正方形EFGH的周长为(　　)　A. B．2C. ＋1 D．2 ＋1
【中考·毕节】如图，正方形ABCD的边长为9，将正方形折叠，使顶点D落在BC边上的点E处，折痕为GH. 若BE∶EC＝2∶1，则线段CH的长是(　　)A．3　　　 B．4　　　 C．5　　　 D．6
例3 如图，正方形ABCD的边长为1 cm，AC为对角线， AE平分∠BAC，EF⊥AC，求BE的长．
线段BE是Rt△ABE的一边，但由于AE未知，不能直接用勾股定理求BE，由条件可证△ABE≌△AFE，问题转化为求EF的长，结合已知条件易获解．
∵四边形ABCD为正方形， ∴∠B＝90°，∠ACB＝45°，AB＝BC＝1 cm. ∵EF⊥AC，∴∠EFA＝∠EFC＝90°. 又∵∠ECF＝45°， ∴△EFC是等腰直角三角形，∴EF＝FC. ∵∠BAE＝∠FAE，∠B＝∠EFA＝90°，AE＝AE， ∴△ABE≌△AFE. ∴AB＝AF＝1 cm，BE＝EF，∴FC＝BE. 在Rt△ABC中，AC ∴FC＝AC－AF＝( －1)(cm)，∴BE＝( －1) cm.
解有关正方形的问题，要充分利用正方形的四边相等、四角相等、对角线垂直平分且相等等性质，正方形的性质、等腰直角三角形的特点、勾股定理是解决正方形的相关证明与计算问题的三把钥匙．
如图，正方形ABCD的对角线AC为菱形AEFC的一边.求∠FAB的度数.
由题意可知∠CAE＝ ∠DAB＝45°.∵在菱形AEFC中，AF平分∠CAE，∴∠FAB＝ ∠CAE＝22.5°.
如图，E是正方形ABCD的边BC的延长线上一点，且CE=BD，AE交DC于点F. 求∠AFC的度数.
连接AC，在正方形ABCD中，AC＝BD，AD∥BC，∠DAC＝∠ACD＝45°.∵BD＝CE，∴AC＝CE.∴∠CAE＝∠CEA.∵AD∥CE，∴∠DAF＝∠AEC.∴∠DAF＝∠CAE＝ ∠DAC＝22.5°.又∵∠ACF＝45°，∴∠AFC＝112.5°.
【中考·河北】如图是边长为10 cm的正方形铁片，过两个顶点剪掉一个三角形，以下四种剪法中，裁剪线长度所标的数据(单位：cm)不正确的是(　　)
【中考·郴州】如图，在正方形ABCD中，△ABE和△CDF为直角三角形，∠AEB＝∠CFD＝90°，AE＝CF＝5，BE＝DF＝12，则EF的长是(　　)A．7 B．8 C．7 D．7
【中考·河南】我们知道：四边形具有不稳定性.如图，在平面直角坐标系中，边长为2的正方形ABCD的边AB在x轴上，AB的中点是坐标原点O，固定点A，B，把正方形沿箭头方向推，使点D落在y轴正半轴上点D′处，则点C的对应点C′的坐标为(　　)A．( ，1) B．(2，1)C．(1， ) D．(2， )
正方形同时具备平行四边形、菱形、矩形的所有性质，因此，正方形的四个角都是直角，四条边都相等，对角线互相垂直平分且相等，每一条对角线平分一组对角，正方形是轴对称图形，有四条对称轴．这些性质为证明线段相等、垂直，角相等提供了重要的依据．
【中考·安顺】如图，正方形ABCD的边长为4，E为BC上的一点，BE＝1，F为AB上的一点，AF＝2，P为AC上一个动点，则PF＋PE的最小值为________．
易错点：不能将两线段和转化为一条线段而致错