





初中数学北师大版七年级下册2 用关系式表示的变量间关系优质课件ppt
展开日晷和土圭是最古老的计时仪器,是一种构造简单,直立于地上的杆子,用以观察太阳光投射的杆影,通过杆影移动规律、影的长短,以定时刻 、冬至、夏至日.
1. 经历探索某些图形中变量之间的关系的过程,体会一个变量对另一个变量的影响,发展符号感.
2. 能根据具体情景,用关系式表示某些变量之间的关系.
3. 能根据关系式求值,初步体会自变量和因变量的数值对应关系.
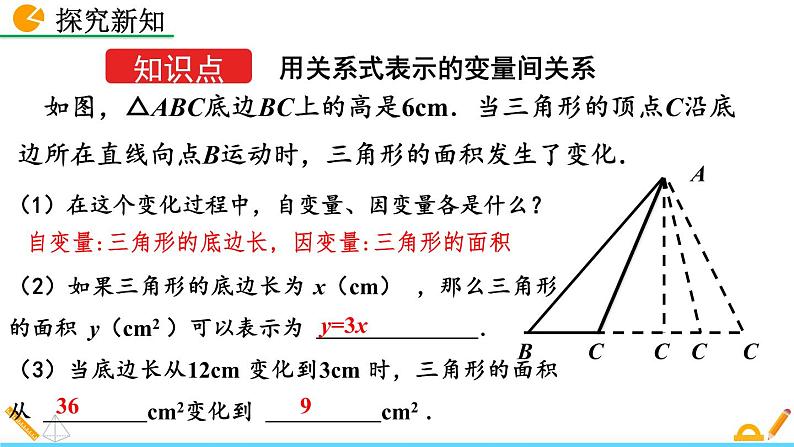
如图,△ABC底边BC上的高是6cm.当三角形的顶点C沿底边所在直线向点B运动时,三角形的面积发生了变化.
(1)在这个变化过程中,自变量、因变量各是什么?(2)如果三角形的底边长为 x(cm) ,那么三角形的面积 y(cm2 )可以表示为 .(3)当底边长从12cm 变化到3cm 时,三角形的面积从 cm2变化到 cm2 .
自变量:三角形的底边长, 因变量:三角形的面积
y=3x表示了图中三角形底边长x和面积y之间的关系,它是变量y随x变化的关系式.
关系式 y=3x
关系式是我们表示变量之间关系的另一种方法.利用关系式,(如y=3x),我们可以根据任何一个自变量的值求出相应的因变量的值.
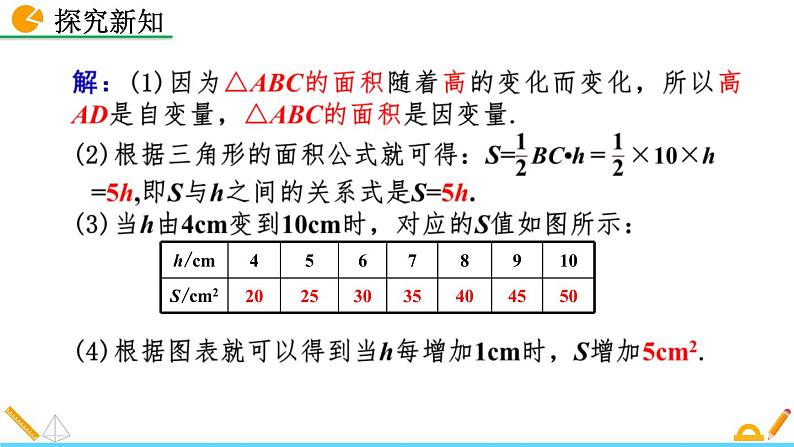
例1 △ABC的底边BC=10 cm,当BC边上的高线AD从小到大变化时,△ABC的面积也随之变化.(1)在这个变化过程中,自变量和因变量各是什么?(2)△ABC的面积S(cm2)与高h(cm)之间的关系式是什么?(3)用表格表示当h由4cm变到10cm时(每次增加1cm),S的相应值.(4)当h每增加1cm时,S如何变化?
用关系式表示面积的变化
优点:简单明了,能准确反映整个变化过程中自变量与因变量的相互关系.缺点:求对应值时有时要经过比较复杂的计算,而且实际问题中,有的变量之间的关系不一定能用关系式表示出来.
用关系式表示变量之间的关系的优缺点是什么?
一块长为5米,宽为2米的长方形木板,现要在长边上截取一边长为x米的一小长方形(如图),则剩余木板的面积y(平方米)与x(米)之间的关系式为( ) A.y=2x B.y=10-2x C.y=5x D.y=10-5x
例2 如图,圆柱的底面直径是2cm,当圆柱的高h cm由大到小变化时,圆柱的体积V(cm3)随之发生变化.(1)在这个变化中,自变量和因变量各是什么?(2)写出圆柱的体积V与高h之间的关系式.(3)当h由10cm变化到5cm时,V是怎样变化的?(4)当h=0时,V等于多少?此时表示什么?
解:(1)自变量是圆柱的高,因变量是圆柱的体积.(2)V=πh.(3)当h=10cm时,V=πh=10πcm3;当h=5cm时,V=πh=5πcm3.所以当h由10cm变化到5cm时,V从10πcm3变化到5πcm3.(4)V=0,此时表示平面图形——直径为2cm的圆.
如图,圆锥的高是4cm,当圆锥的底面半径由小到大变化时,圆锥的体积也随之发生了变化.
(1)在这个变化过程中,自变量、因变量各是什么?(2)如果圆锥底面半径为r (cm) ,那么圆锥的体积 V(cm 3 )与r的关系式为 .(3)当底面半径由 1 cm 变化到10 cm 时,圆锥的体积由 cm 3 变化到 cm 3 .
自变量:圆锥底面半径, 因变量:圆锥的体积
你知道什么是“低碳生活”吗? “低碳生活”是指人们生活中尽量减少所耗能量,从而降低碳、特别是二氧化碳的排放量的一种生活方式.
排碳计算公式家居用电的二氧化碳排放量(kg)=耗电量(kW · h)×0.785开私家车的二氧化碳排放量(kg)=耗油量(L)× 2.7家用天然气二氧化碳排放量(kg)=天然气使用量(m3 )× 0.19家用自来水二氧化碳排放量(kg)=自来水使用量(t)× 0.91
(1)家居用电的二氧化碳排放量可以用关系式表示为 ,其中的字母表示 .(2)在上述关系式中,耗电量每增加1kW·h,二氧化碳排放量增加 .当耗电量从1kW · h增加到100kW·h时,二氧化碳排放量从 增加到 .
二氧化碳排放量和用电量
(3)小明家本月用电大约110kW·h、天然气20m3 、自来水5t、耗油75L,请你计算一下小明家这几项的二氧化碳排放量.
y=110×0.785+20×0.19+5×0.91+75×2.7=297.2kg
(2019•柳州)已知A、B两地相距3千米,小黄从A地到B地,平均速度为4千米/小时,若用x表示行走的时间(小时),y表示余下的路程(千米),则y关于x的关系式是( )A.y=4x(x≥0) B.y=4x﹣3(x≥0)C.y=3﹣4x(x≥0)D.y=3﹣4x(0≤x≤0.75)
1.在半径为4的圆中,挖去一个边长为x的正方形,剩下部分面积为y,则关于y与x之间的关系式为( )A.y=πx2-4yB.y=16π-x2C.y=16-x2D.y=x2-4y
2.长方形的周长为24 cm,其中一边长为x cm(其中x>0),面积为y cm2,则在这样的长方形中,y与x的关系式可以写为( )A.y=x2 B.y=(12-x2)C.y=(12-x)x D.y=2(12-x)
3.如图是一个简单的数值运算程序,当输入x的值为1时,则输出的数值为____.4.在关系式S=40t中,当t=1.5时,S=____.
5.某公司现年产量为100万件,计划以后每年增加2万件,则年产量y(万件)与年数(x)之间的关系是____________;自变量是____,因变量是____;常量是______.
已知三峡大坝泄洪时每孔水流量为1500立方米/秒,上游水位为40米,水位每降低1米,下游水位升高0.2米.(1)你能说出这个变化过程中的自变量和因变量是什么吗?(2)如果下游水位升高G米,泄洪后上游水位高度为h米,试列出G和h的关系式.
解 :(1)自变量是上游水位下降情况,因变量是下游水位升高高度.
对于气温,有的地方用摄氏温度表示,有的地方用华氏温度表示,摄氏温度x(℃)与华氏温度y(°F)之间存在的关系为:y=1.8x+32,如图所示:(1)用表格表示当x从-10到30(每次增加10),y的相应的值.(2)某天,连云港的最高气温是8℃,悉尼的最高气温是91°F,问这一天悉尼的最高气温比连云港的最高气温高多少摄氏度(结果保留整数)?
解:(1)(2)y=91,则1.8x+32=91,所以有x≈33.所以这一天悉尼的最高气温比连云港的高33-8=25(℃).
2、列表与列关系式表示变量之间的关系各有 什么特点?
1、到今天为止我们一共学了几种方法来表示 自变量与因变量之间的关系?
列表格与列关系式两种方法
通过列表格,可以较直观地表示因变量随自变量变化而变化的情况. 利用关系式,我们可以根据一个自变量的值求出相应的因变量的值 .
北师大版七年级下册2 用关系式表示的变量间关系教学演示ppt课件: 这是一份北师大版七年级下册<a href="/sx/tb_c77851_t3/?tag_id=26" target="_blank">2 用关系式表示的变量间关系教学演示ppt课件</a>,共15页。PPT课件主要包含了y3x,因变量,含自变量的代数式,y0785x,785kg,5kg,y=04x,距地面的高度,空中的气温等内容,欢迎下载使用。
北师大版七年级下册2 用关系式表示的变量间关系背景图课件ppt: 这是一份北师大版七年级下册2 用关系式表示的变量间关系背景图课件ppt,共31页。PPT课件主要包含了三角形的底和高,y3x,三角形底边长,三角形面积,三角形底边边长x,面积y,含自变量代数式,因变量,系数为1,其中的字母表示什么等内容,欢迎下载使用。
初中数学北师大版七年级下册2 用关系式表示的变量间关系教案配套课件ppt: 这是一份初中数学北师大版七年级下册2 用关系式表示的变量间关系教案配套课件ppt,共21页。PPT课件主要包含了课前复习,探索新知,BC的长,△ABC的面积,y3x,做一做,圆锥的高,圆锥的体积,巩固练习,S12x等内容,欢迎下载使用。













