初中数学鲁教版 (五四制)八年级下册1 菱形的性质与判定备课ppt课件

这是一份初中数学鲁教版 (五四制)八年级下册1 菱形的性质与判定备课ppt课件，共14页。PPT课件主要包含了证明命题的一般步骤，四边形之间有何关系，∴ABAD，2×△ABD的面积，∴∠AED900，∵ABAD，∴AOCO，∵AC⊥BD，∴DADC等内容，欢迎下载使用。

第六章 特殊的平行四边形 1、菱形的性质及判定（1）
(1)理解题意:分清命题的条件(已知),结论(求证);
(2)根据题意,画出图形;
(3)结合图形,用符号语言写出“已知”和“求证”;
(4)分析题意,探索证明思路(由“因”导“果”,执“果”索“因”.);
(5)依据思路,运用数学符号和数学语言条理清晰地写出证明过程;
(6)检查表达过程是否正确,完善.
定理:平行四边形的对边相等.
证明后的结论,以后可以直接运用.
∵四边形ABCD是平行四边形.∴AB=CD,BC=DA.
定理:平行四边形的对角相等.
∵四边形ABCD是平行四边形.∴∠A=∠C, ∠B=∠D.
定理:平行四边形的对角线互相平分.
∵四边形ABCD是平行四边形.∴CO=AO,BO=DO.
定理:夹在两条平等线间的平等线段相等.
∵MN∥PQ,AB∥CD,∴AB=CD.
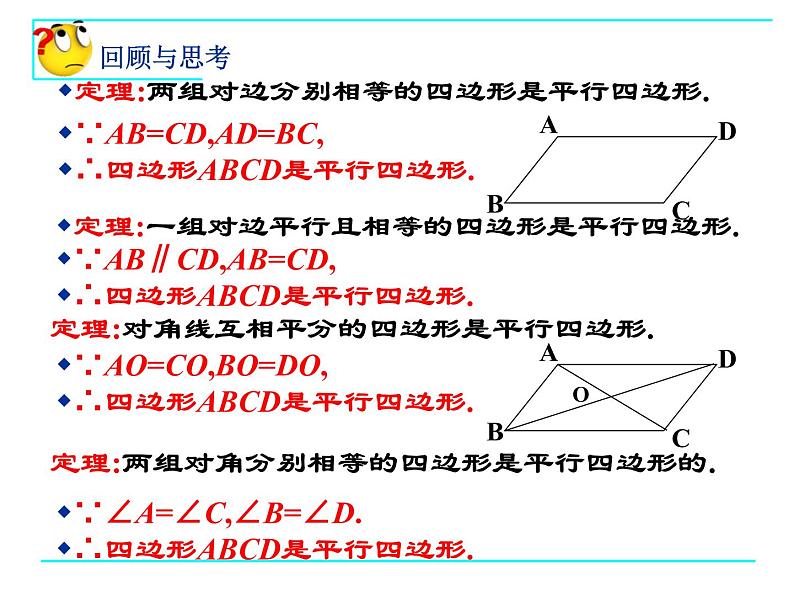
定理:两组对边分别相等的四边形是平行四边形.
定理:一组对边平行且相等的四边形是平行四边形.
定理:对角线互相平分的四边形是平行四边形.
定理:两组对角分别相等的四边形是平行四边形的.
∵AB=CD,AD=BC,∴四边形ABCD是平行四边形.
∵AB∥CD,AB=CD,∴四边形ABCD是平行四边形.
∵AO=CO,BO=DO,∴四边形ABCD是平行四边形.
∵∠A=∠C,∠B=∠D.∴四边形ABCD是平行四边形.
特殊的平行四边形之间呢？
还记得它们与平行四边形的关系吗?
能用一张图来表示它们之间的关系吗?
定理:菱形的四条边都相等.
已知:如图,四边形ABCD是菱形.
分析:由菱形的定义,利用平行四边形性质可使问题得证.
∵ 四边形ABCD是菱形,
∴AB=CD,AD=BC.
求证:AB=BC=CD=DA.
∴ AB=BC=CD=AD.
∵四边形ABCD是平行四边形
定理:菱形的两条对角线互相垂直,并且每条对角线平分一组对角.
已知:如图,AC,BD是菱形ABCD的两条对角线,AC,BD相交于点O.
求证: (1).AC⊥BD; (2).AC平分∠BAD和∠BCD, BD平分∠ADC和∠ABC.
∴AD=CD,AO=CO.
分析:根据平行四边形对角线互相平分和等腰三角形“三线合一”来证明.
∴△AOD≌△COD(SSS).
∴∠AOD=∠COD=900.
(2)∵AD=AB,DA=DC,AC⊥BD;
∴AC平分∠BAD和∠BCD,BD平分∠ADC和∠ABC.
已知:如图,四边形ABCD是边长为13cm的菱形,其中对角线BD长10cm.
求:(1).对角线AC 的长度;(2).菱形ABCD 的面积.
∵四边形ABCD是菱形,
(2)菱形ABCD的面积=△ABD的面积+△CBD的面积
∴AC=2AE=2×12=24(cm).
定理:四条边都相等的四边形是菱形.
已知:如图,在四边形ABCD中, AB=BC=CD=DA..
分析:利用菱形定义和两组对边分别相等的四边形是平行四边形,可使问题得证.
∵AB=BC=CD=DA,
∴AB=CD,BC=DA.
∴四边形ABCD是平行四边形..
求证:四边形ABCD是菱形.
∴四边形ABCD是菱形.
定理:对角线互相垂直的平行四边形是菱形.
已知:如图,在□ABCD中,对角线AC⊥BD.
分析:要证明□ABCD是菱形,就要证明有一组邻边相等即可.
∵四边形ABCD是平行四边形.
∴AB=BC=CD=AD.
∵AC,BD是菱形ABCD的两条对角线.
∴AC⊥BD,AC平分∠BAD和∠BCD,BD平分∠ADC和∠ABC.
在四边形ABCD中, ∵AB=BC=CD=AD,
∵AC,BD是□ABCD的两条对角线,AC⊥BD.