人教版八年级下册17.1 勾股定理说课ppt课件

这是一份人教版八年级下册17.1 勾股定理说课ppt课件，共15页。PPT课件主要包含了SP+SQSR，a2+b2c2，勾股定理，毕达哥拉斯定理，勾股世界等内容，欢迎下载使用。

这是1955年希腊曾经发行的纪念一位数学家的邮票。
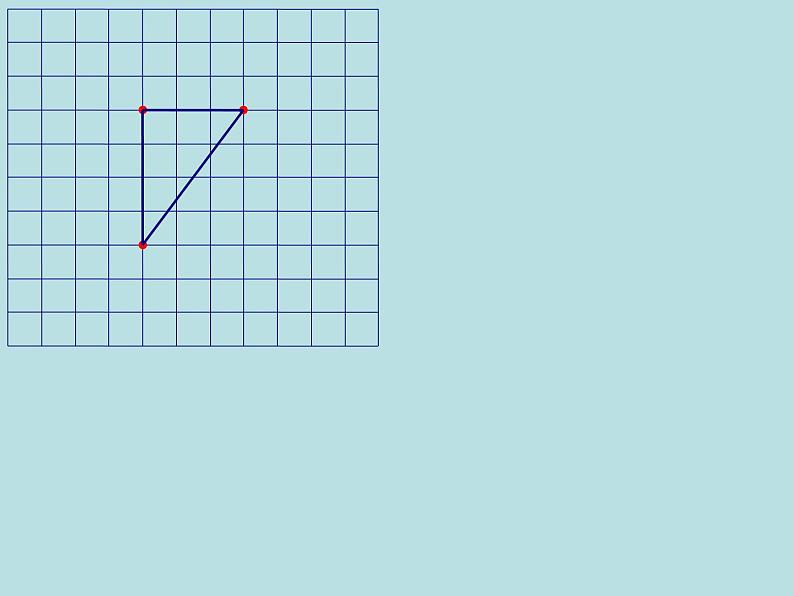
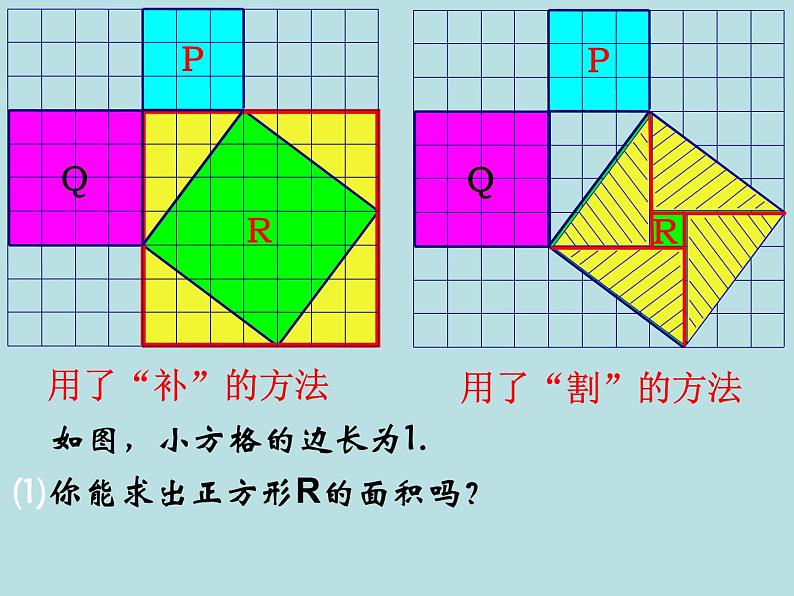
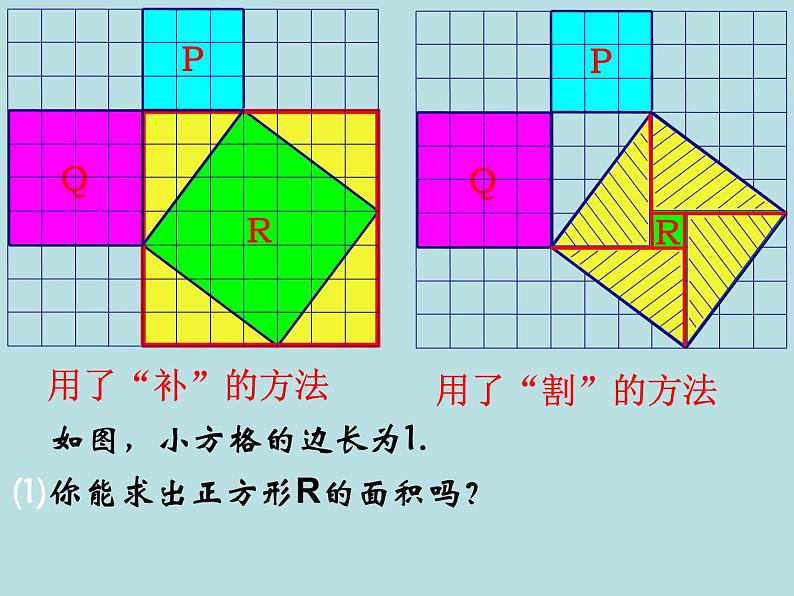
如图，小方格的边长为1.
(1)你能求出正方形R的面积吗？
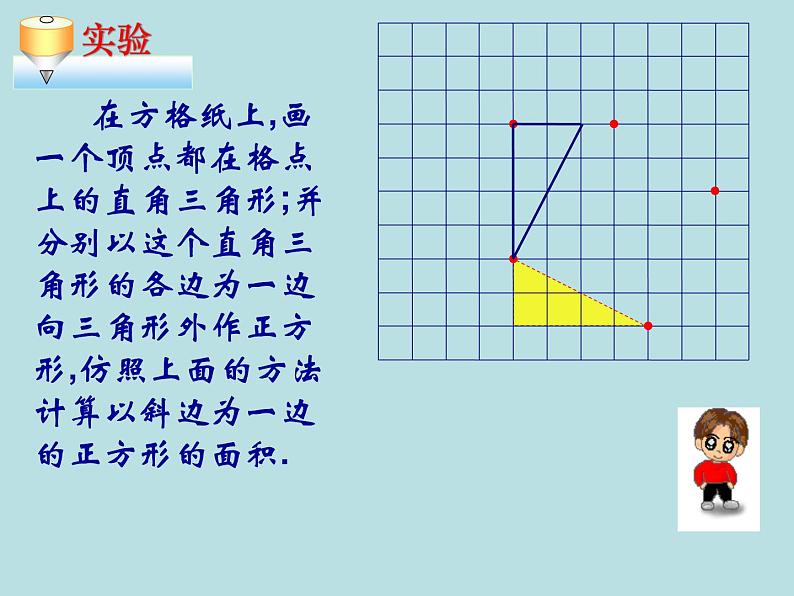
在方格纸上,画一个顶点都在格点上的直角三角形;并分别以这个直角三角形的各边为一边向三角形外作正方形,仿照上面的方法计算以斜边为一边的正方形的面积.
观察所得到的各组数据，你有什么发现？
猜想:两直角边a、b与斜边c 之间的关系？
猜想两直角边a、b与斜边c 之间的关系？
直角三角形两直角边的平方和等于斜边的平方.
两千多年前，古希腊有个哥拉
斯学派，他们首先发现了勾股定理，因此
在国外人们通常称勾股定理为毕达哥拉斯
年希腊曾经发行了一枚纪念票。
定理。为了纪念毕达哥拉斯学派，1955
国家之一。早在三千多年前，
国家之一。早在三千多年前
两千多年前，古希腊有个毕达哥拉斯学派，他们首先发现了勾股定理，因此在国外人们通常称勾股定理为毕达哥拉斯定理。为了纪念毕达哥拉斯学派，1955年希腊曾经发行了一枚纪念邮票。
我国是最早了解勾股定理的国家之一。早在三千多年前，周朝数学家商高就提出，将一根直尺折成一个直角，如果勾等于三，股等于四，那么弦就等于五，即“勾三、股四、弦五”，它被记载于我国古代著名的数学著作《周髀算经》中。
1.求下列图中表示边的未知数x、y、z的值.
2.求下列直角三角形中未知边的长:
可用勾股定理建立方程.
A.8 米 B.9 米 C.10米 D.14米
１、如图,一个长8 米,宽6 米的草地,需在相对角的顶点间加一条小路,则小路的长为 ( )