数学北师大版第一章 特殊平行四边形综合与测试优秀单元测试课后作业题

这是一份数学北师大版第一章 特殊平行四边形综合与测试优秀单元测试课后作业题，共10页。试卷主要包含了选择题，填空题，解答题，综合题等内容，欢迎下载使用。

一、选择题


LISTNUM OutlineDefault \l 3 下列说法中正确的是（ ）


A.四边相等的四边形是菱形


B.一组对边相等，另一组对边平行的四边形是菱形


C.对角线互相垂直的四边形是菱形


D.对角线互相平分的四边形是菱形





LISTNUM OutlineDefault \l 3 能判定一个四边形是菱形的条件是（ ）


A.对角线互相平分且相等


B.对角线互相垂直且相等


C.对角线互相垂直且对角相等


D.对角线互相垂直，且一条对角线平分一组对角


LISTNUM OutlineDefault \l 3 对角线相等且互相平分的四边形是（ ）


A.一般四边形 B.平行四边形 C.矩形 D.菱形


LISTNUM OutlineDefault \l 3 在四边形ABCD中，AC与BD相交于点O，且OA=OC，OB=OD．如果再增加条件AC=BD，此四边形一定是（ ）


A．正方形 B．矩形 C．菱形 D．都有可能


LISTNUM OutlineDefault \l 3 在四边形ABCD中，AC、BD交于点O，在下列各组条件中，不能判定四边形ABCD为矩形的是（ ）


A．AB=CD，AD=BC，AC=BD


B．AO=CO，BO=DO，∠A=90°


C．∠A=∠C，∠B+∠C=180°，AC⊥BD


D．∠A=∠B=90°，AC=BD


LISTNUM OutlineDefault \l 3 如图，矩形ABCD的顶点A、C分别在直线a、b上，且a∥b，∠1=60°，则∠2的度数为（ ）





A．30° B．45° C．60° D．75°





LISTNUM OutlineDefault \l 3 矩形具有而平行四边形不一定具有的性质是（ ）


A.对角相等 B.对边相等 C.对角线相等 D.对角线互相平分


LISTNUM OutlineDefault \l 3 如图，矩形的两条对角线的一个交角为60°，两条对角线的长度的和为20cm，则这个矩形的一条较短边的长度为（ ）





A.10cm B.8cm C.6cm D.5cm





LISTNUM OutlineDefault \l 3 如图，在菱形ABCD中，M，N分别在AB，CD上，且AM=CN，MN与AC交于点O，连接BO.若∠DAC=28°，则∠OBC的度数为( )





A.28° B.52° C.62° D.72°


LISTNUM OutlineDefault \l 3 如图，菱形ABCD周长为20，对角线AC、BD相交于点O，E是CD的中点，则OE的长是( )





A．2.5 B．3 C．4 D．5





LISTNUM OutlineDefault \l 3 如图，在菱形ABCD中，∠ABC=60°，AB=1，E为BC的中点，则对角线BD上的动点P到E、C两点的距离之和的最小值为（ ）











LISTNUM OutlineDefault \l 3 将一张正方形纸片按如图步骤，通过折叠得到图④，再沿虚线剪去一个角，展开铺平后得到图⑤，其中FM，GN是折痕．若正方形EFGH与五边形MCNGF的面积相等，则的值是（ ）





A． B．﹣1 C． D．








二、填空题


LISTNUM OutlineDefault \l 3 如图，在矩形ABCD中，AE⊥BD于E,∠DAE=3∠EAB，则∠ACD的度数为 ．








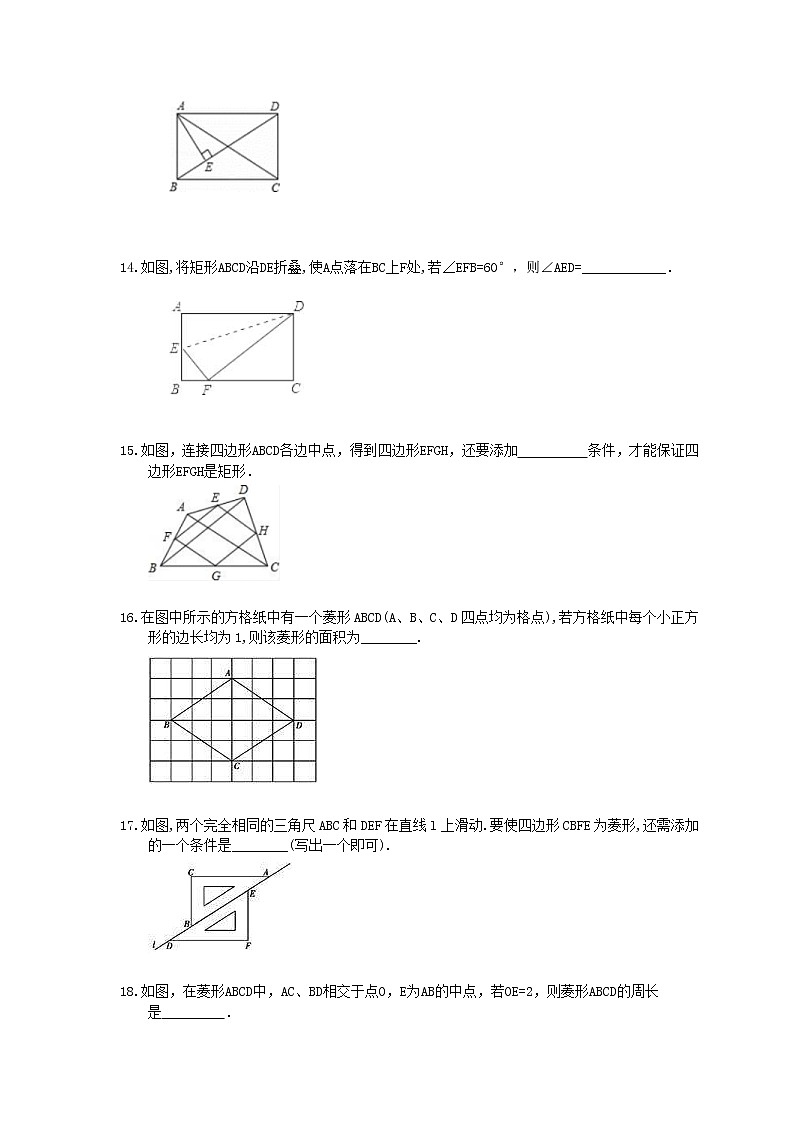
LISTNUM OutlineDefault \l 3 如图,将矩形ABCD沿DE折叠,使A点落在BC上F处,若∠EFB=60°，则∠AED=____________．








LISTNUM OutlineDefault \l 3 如图，连接四边形ABCD各边中点，得到四边形EFGH，还要添加 条件，才能保证四边形EFGH是矩形．








LISTNUM OutlineDefault \l 3 在图中所示的方格纸中有一个菱形ABCD(A、B、C、D四点均为格点),若方格纸中每个小正方形的边长均为1,则该菱形的面积为________.








LISTNUM OutlineDefault \l 3 如图,两个完全相同的三角尺ABC和DEF在直线l上滑动.要使四边形CBFE为菱形,还需添加的一个条件是________(写出一个即可).








LISTNUM OutlineDefault \l 3 如图，在菱形ABCD中，AC、BD相交于点O，E为AB的中点，若OE=2，则菱形ABCD的周长是 ．








LISTNUM OutlineDefault \l 3 若正方形的面积是9，则它的对角线长是 .


LISTNUM OutlineDefault \l 3 在平面直角坐标系中，直线l：y=x+1与y轴交于点A1，如图所示，依次作正方形OA1B1C1，正方形C1A2B2C2，正方形C2A3B3C3，正方形C3A4B4C4，……，点A1，A2，A3，A4，……在直线l上，点C1，C2，C3，C4，……在x轴正半轴上，则前n个正方形对角线长的和是 ．














三、解答题


LISTNUM OutlineDefault \l 3 如图，四边形ABCD中，对角线AC、BD相交于点O，AO=CO，BO=DO，且∠ABC+∠ADC=180°。


（1）求证：四边形ABCD是矩形;


（2）若∠ADF:∠FDC=3:2，DF⊥AC，则∠BDF的度数是多少？


























LISTNUM OutlineDefault \l 3 如图在菱形ABCD中,对角线AC、BD相交于点O,过点D作对角线BD的垂线交BA的延长线于点E.


(1)证明:四边形ACDE是平行四边形;


(2)若AC=8,BD=6,求△ADE的周长.





























LISTNUM OutlineDefault \l 3 如图,在平行四边形ABCD中,用直尺和圆规作∠BAD的平分线交BC于点E(尺规作图的痕迹保留在图中了),连接EF．


（1）求证：四边形ABEF为菱形；


（2）AE，BF相交于点O，若BF=6，AB=5，求AE的长．








LISTNUM OutlineDefault \l 3 如图，已知在矩形ABCD中，M、N分别是边AD、BC的中点，E、F分别是线段BM、CM的中点.


（1）求证：△ABM≌△DCM；


（2）填空：当AB：AD= 时，四边形MENF是正方形.








LISTNUM OutlineDefault \l 3 如图，在Rt△ABC中，AD是边BC上的中线，过点A作AE∥BC，过点D作DE∥AB，DE与AC、AE分别交于点O、点E，连结EC．


（1）求证：AD=EC；


（2）求证：四边形ADCE是菱形；


（3）若AB=AO，求OD:OA的值．











四、综合题


LISTNUM OutlineDefault \l 3 已知E,F分别为正方形ABCD的边BC,CD上的点,AF,DE相交于点G,当E,F分别为边BC,CD的中点时,有AF=DE,AF⊥DE成立.


试探究下列问题:


(1)如图①,若点E不是边BC的中点,F不是边CD的中点,且CE=DF,上述结论是否仍然成立?(请直接回答“成立”或“不成立”,不需要证明)


(2)如图②,若点E,F分别在CB的延长线和DC的延长线上,且CE=DF,此时,上述结论是否仍然成立?若成立,请写出证明过程,若不成立,请说明理由;


(3)如图③,在(2)的基础上,连接AE和EF,若点M,N,P,Q分别为AE,EF,FD,AD的中点,请判断四边形MNPQ是“矩形、菱形、正方形”中的哪一种,并证明你的结论.
































参考答案


LISTNUM OutlineDefault \l 3 \s 1 A


LISTNUM OutlineDefault \l 3 C


LISTNUM OutlineDefault \l 3 C．


LISTNUM OutlineDefault \l 3 B


LISTNUM OutlineDefault \l 3 C


LISTNUM OutlineDefault \l 3 C


LISTNUM OutlineDefault \l 3 C.


LISTNUM OutlineDefault \l 3 D


LISTNUM OutlineDefault \l 3 C


LISTNUM OutlineDefault \l 3 答案为：A.


LISTNUM OutlineDefault \l 3 C


LISTNUM OutlineDefault \l 3 答案为：A．


解析：连接HF，设直线MH与AD边的交点为P，如图：





由折叠可知点P、H、F、M四点共线，且PH=MF，


设正方形ABCD的边长为2a，则正方形ABCD的面积为4a2，


∵若正方形EFGH与五边形MCNGF的面积相等


∴由折叠可知正方形EFGH的面积=×正方形ABCD的面积=，


∴正方形EFGH的边长GF==∴HF=GF=


∴MF=PH==a∴=a÷=


LISTNUM OutlineDefault \l 3 答案为：67.5°，


LISTNUM OutlineDefault \l 3 答案为：75°





LISTNUM OutlineDefault \l 3 答案为：AC⊥BD





LISTNUM OutlineDefault \l 3 答案为：12；





LISTNUM OutlineDefault \l 3 答案为：C；B=BF或BE⊥CF或∠EBF=60°或BD=BF(答案不唯一)





LISTNUM OutlineDefault \l 3 答案为：16．





LISTNUM OutlineDefault \l 3 答案为：3


LISTNUM OutlineDefault \l 3 答案为： (2n﹣1).


解析：由题意可得，


点A1的坐标为(0，1)，点A2的坐标为(1，2)，点A3的坐标为(3，4)，


点A4的坐标为(7，8)，……，


∴OA1=1，C1A2=2，C2A3=4，C3A4=8，……，


∴前n个正方形对角线长的和是：


(OA1+C1A2+C2A3+C3A4+…+Cn﹣1An)= (1+2+4+8+…+2n﹣1)，


设S=1+2+4+8+…+2n﹣1，则2S=2+4+8+…+2n﹣1+2n，则2S﹣S=2n﹣1，


∴S=2n﹣1，∴1+2+4+8+…+2n﹣1=2n﹣1，


∴前n个正方形对角线长的和是：×(2n﹣1)，故答案为： (2n﹣1)，





LISTNUM OutlineDefault \l 3 （1）证明：∵AO=CO，BO=DO，


∴四边形ABCD是平行四边形，


∴∠ABC=∠ADC，


∵∠ABC+∠ADC=180°，


∴∠ABC=∠ADC=90°，


∴四边形ABCD是矩形；


（2）解：∵∠ADC=90°，∠ADF∶∠FDC=3∶2，


∴∠FDC=36°，


∵DF⊥AC，


∴∠DCO=90°﹣36°=54°，


∵四边形ABCD是矩形，


∴OC=OD，


∴∠ODC=54°，


∴∠BDF=∠ODC﹣∠FDC=18°．





LISTNUM OutlineDefault \l 3 解：(1)证明:∵四边形ABCD是菱形,


∴AB∥CD,AC⊥BD,


∴AE∥CD,∠AOB=90°,


又∵DE⊥BD,即∠EDB=90°,


∴∠AOB=∠EDB.


∴DE∥AC.


∴四边形ACDE是平行四边形.


(2)∵四边形ABCD是菱形,AC=8,BD=6,


∴AO=4,DO=3,


∴AD=CD=5.


又∵四边形ACDE是平行四边形,


∴AE=CD=5,DE=AC=8.


∴△ADE的周长为AD+AE+DE=5+5+8=18.





LISTNUM OutlineDefault \l 3 （1）证明：由尺规作∠BAF的角平分线的过程可得AB=AF，∠BAE=∠FAE，


∵四边形ABCD是平行四边形，


∴AD∥BC，∴∠FAE=∠AEB，∴∠BAE=∠AEB，


∴AB=BE，∴BE=FA，∴四边形ABEF为平行四边形，


∵AB=AF，∴四边形ABEF为菱形；


（2）解：∵四边形ABEF为菱形，


∴AE⊥BF，BO=FB=3，AE=2AO，


在Rt△AOB中，AO=4，∴AE=2AO=8．





LISTNUM OutlineDefault \l 3 （1）证明：∵四边形ABCD是矩形，∴AB=DC，∠A=∠D=90°，


∵M为AD的中点，∴AM=DM，


在△ABM和△DCM中∴△ABM≌△DCM（SAS）


（2）解：当AB：AD=1：2时，四边形MENF是正方形，


理由是：∵AB：AD=1：2，AM=DM，AB=CD，∴AB=AM=DM=DC，


∵∠A=∠D=90°，∴∠ABM=∠AMB=∠DMC=∠DCM=45°，∴∠BMC=90°，


∵四边形ABCD是矩形，∴∠ABC=∠DCB=90°，∴∠MBC=∠MCB=45°，∴BM=CM，


∵N、E、F分别是BC、BM、CM的中点，∴BE=CF，ME=MF，NF∥BM，NE∥CM，


∴四边形MENF是平行四边形，


∵ME=MF，∠BMC=90°，∴四边形MENF是正方形，


即当AB：AD=1：2时，四边形MENF是正方形，


故答案为：1：2.





LISTNUM OutlineDefault \l 3 解：


（1）证明：∵AE∥BC，DE∥AB，∴四边形ABDE为平行四边形，∴AE=BD，


∵在Rt△ABC中，AD是斜边BC上的中线，∴AD=CD=BD，∴AE=CD，.Cm]


又∵AE∥CD，∴四边形ADCE为平行四边形，∴AD=EC；


（2）由（1）可知，四边形ADCE为平行四边形，且AD=CD，


∴平行四边形ADCE为菱形；


（3）∵四边形ADCE为平行四边形，∴AC与ED互相平分，


∴点O为AC的中点，


∵AD是边BC上的中线，∴点D为BC边中点，


∴OD为△ABC的中位线，


∵AB=AO，∴AO=2OD，即OD:OA的值为1：2．











四、综合题


LISTNUM OutlineDefault \l 3 解：(1)成立.


(2)成立.理由:∵四边形ABCD为正方形,∴AD=DC,∠BCD=∠ADC=90°.


在△ADF和△DCE中,DF=CE,∠ADC=∠BCD,AD=CD∴△ADF≌△DCE(SAS),


∴AF=DE,∠DAF=∠CDE.


∵∠ADG+∠EDC=90°,∴∠ADG+∠DAF=90°,∴∠AGD=90°,即AF⊥DE.


(3)四边形MNPQ是正方形.


理由:如图,设MQ交AF于点O,PQ交DE于点H,


∵点M,N,P,Q分别为AE,EF,FD,AD的中点,


∴MQ=PN= SKIPIF 1 < 0 DE,PQ=MN= SKIPIF 1 < 0 AF,MQ∥DE∥PN,PQ∥AF∥MN,


∴四边形GHQO是平行四边形,


∵AF=DE,∴MQ=PQ=PN=MN,∴四边形MNPQ是菱形.


∵AF⊥DE,∴∠AGD=90°,∴∠HQO=∠AOQ=∠AGD=90°,


∴四边形MNPQ是正方形.