【培优分级练】北师大版数学九年级上册 第06课《特殊平行四边形解答题（难点1-动态几何）》培优三阶练（含解析）

这是一份【培优分级练】北师大版数学九年级上册 第06课《特殊平行四边形解答题（难点1-动态几何）》培优三阶练（含解析）

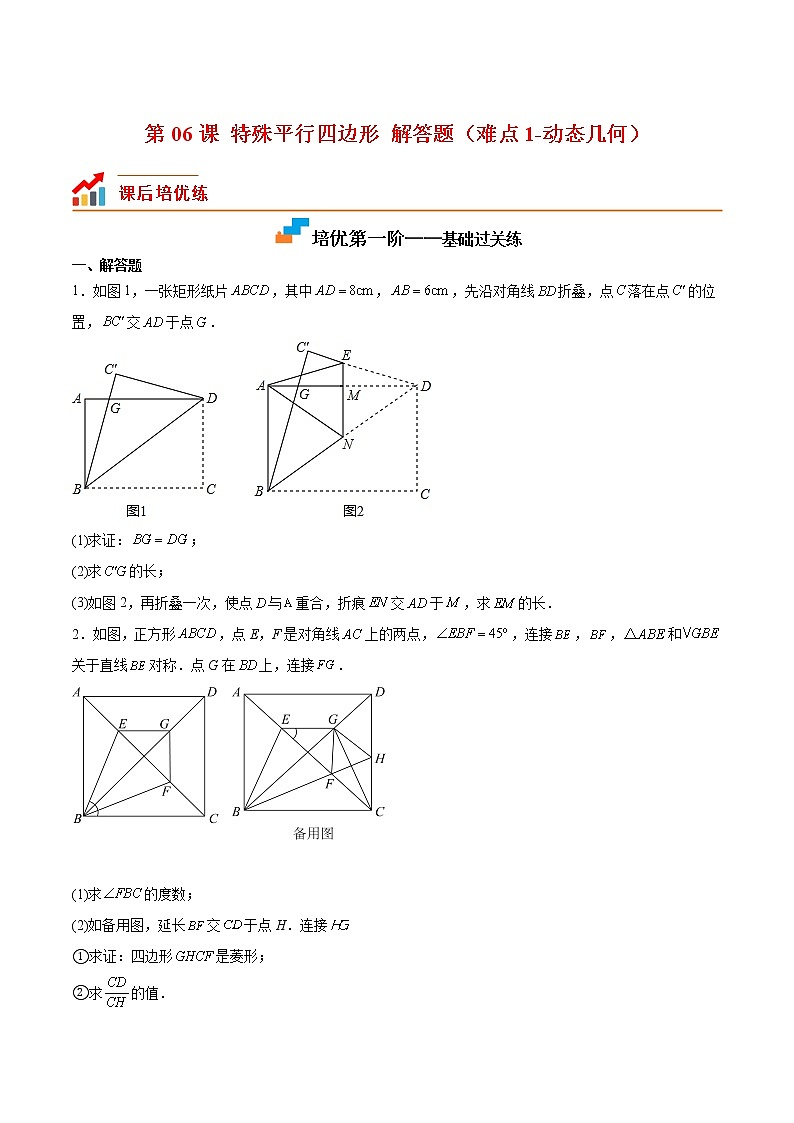
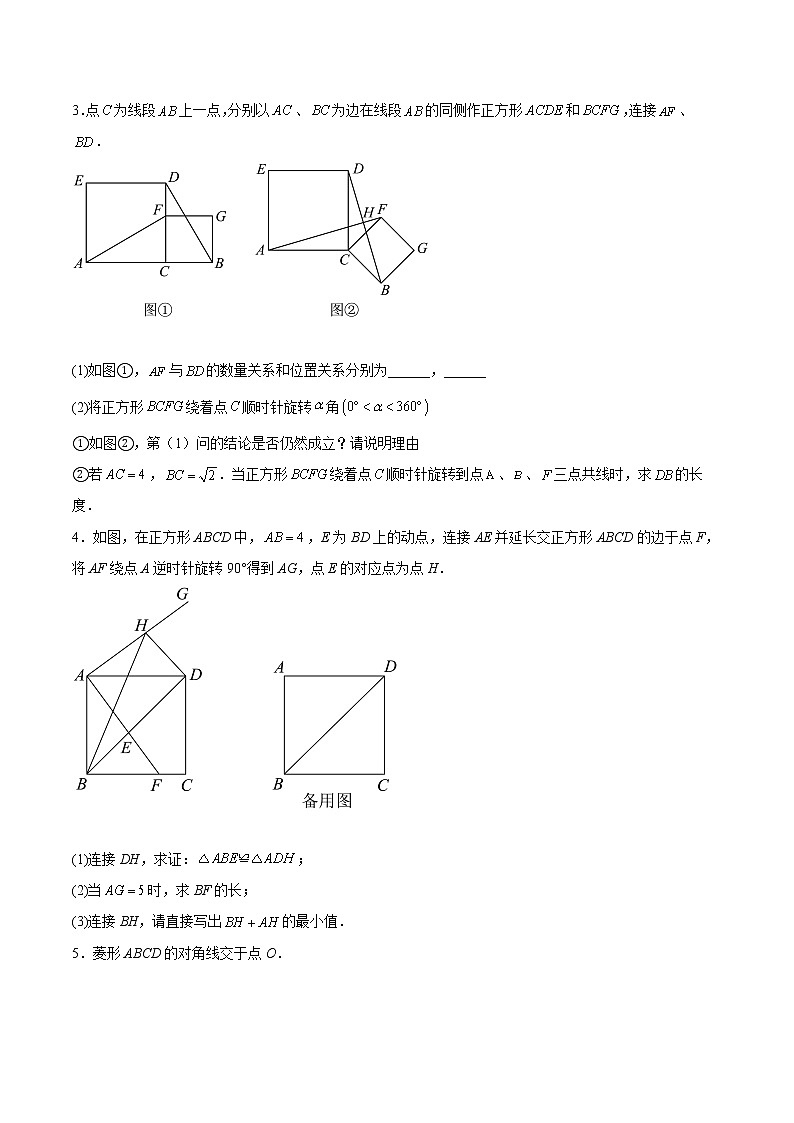
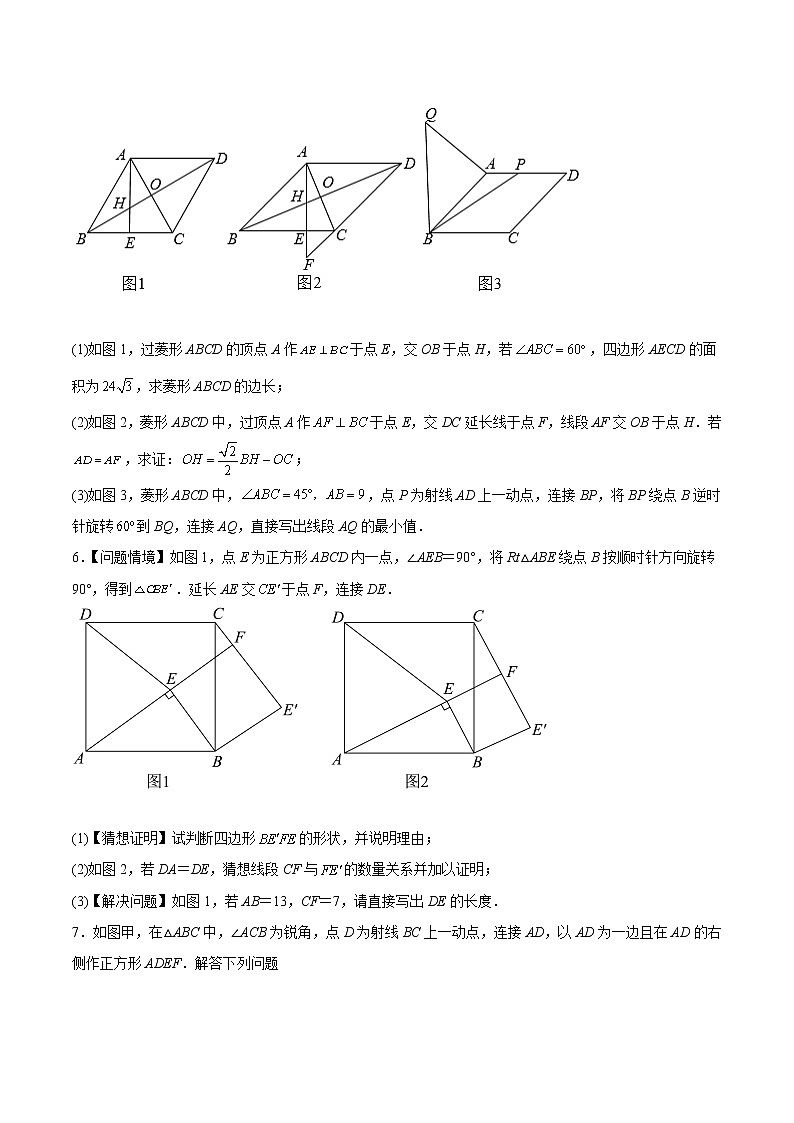
第06课 特殊平行四边形 解答题（难点1-动态几何）课后培优练级练培优第一阶——基础过关练一、解答题1．如图1，一张矩形纸片，其中，，先沿对角线折叠，点落在点的位置，交于点．(1)求证：；(2)求的长；(3)如图2，再折叠一次，使点与重合，折痕交于，求的长．2．如图，正方形，点E，F是对角线上的两点，，连接，，和关于直线对称．点G在上，连接．(1)求的度数；(2)如备用图，延长交于点H．连接①求证：四边形是菱形；②求的值．3．点为线段上一点，分别以、为边在线段的同侧作正方形和，连接、．(1)如图①，与的数量关系和位置关系分别为______，______(2)将正方形绕着点顺时针旋转角①如图②，第（1）问的结论是否仍然成立？请说明理由②若，．当正方形绕着点顺时针旋转到点、、三点共线时，求的长度．4．如图，在正方形ABCD中，，E为BD上的动点，连接AE并延长交正方形ABCD的边于点F，将AF绕点A逆时针旋转90°得到AG，点E的对应点为点H．(1)连接DH，求证：；(2)当时，求BF的长；(3)连接BH，请直接写出的最小值．5．菱形ABCD的对角线交于点O．(1)如图1，过菱形ABCD的顶点A作于点E，交OB于点H，若，四边形AECD的面积为，求菱形ABCD的边长；(2)如图2，菱形ABCD中，过顶点A作于点E，交DC延长线于点F，线段AF交OB于点H．若，求证：；(3)如图3，菱形ABCD中，，点P为射线AD上一动点，连接BP，将BP绕点B逆时针旋转到BQ，连接AQ，直接写出线段AQ的最小值．6．【问题情境】如图1，点E为正方形ABCD内一点，∠AEB＝90°，将Rt△ABE绕点B按顺时针方向旋转90°，得到．延长AE交于点F，连接DE．(1)【猜想证明】试判断四边形的形状，并说明理由；(2)如图2，若DA＝DE，猜想线段CF与的数量关系并加以证明；(3)【解决问题】如图1，若AB＝13，CF＝7，请直接写出DE的长度．7．如图甲，在△ABC中，∠ACB为锐角，点D为射线BC上一动点，连接AD，以AD为一边且在AD的右侧作正方形ADEF．解答下列问题(1)如果AB＝AC，∠BAC＝90°，①当点D在线段BC上时（与点B不重合），如图乙，线段CF、BD之间的位置关系为 ，数量关系为 ．②当点D在线段BC的延长线上时，如图丙，①中的结论是否仍然成立，为什么？(2)如果AB≠AC，∠BAC≠90°点D在线段BC上运动．试探究：当△ABC满足一个什么条件时，CF⊥BC（点C、F重合除外）？并说明理由．8．如图，在矩形ABCD中，AB＝3，AD＝5，作△EDF≌△ADB．　　 　(1)如图1，当点E落在BC边上时，求BE的长．(2)如图2，当点E落在线段BF上时，DE与BC交于点G，求BG的长．(3)记K为BD的中点，S为△KEF的面积，求S的取值范围．9．综合与实践几位同学尝试用矩形纸条ABCD（如图1）折出常见的中心对称图形．(1)如图2，小明将矩形纸条先对折，使AB和DC重合，展开后得折痕EF，再折出四边形ABEF和CDEF的对角线，它们的对角线分别相交于点G，H，最后将纸片展平，则四边形EGFH的形状一定是_______．(2)如图3，小华将矩形纸片沿EF翻折，使点C，D分别落在矩形外部的点，处，F与AD交于点G，延长E交BC于点H，求证：四边形EGFH是菱形．(3)如图4，小美将矩形纸条两端向中间翻折，使得点A，C落在矩形内部的点A′，处，点B，D落在矩形外部的点，处，折痕分别为EF，GH，且点H，，，F在同一条直线上，直接写出四边形EFGH的形状________．10．在中，为锐角，点D为射线BC上一动点，连接AD，以AD为一边且在AD的右侧作正方形ADEF．解答下列问题：(1)如果，①如图1，当点D在线段BC上时（与点B不重合），线段CF、BD之间的位置关系为 ；数量关系为 ；②如图2，当点D在线段BC的延长线上时，①中的结论是否仍然成立，并说明理由；(2)如图3，如果，点D在线段BC上运动（与点B不重合）．试探究：当时，（1）中的CF，BD之间的位置关系是否仍然成立，并说明理由．11．如图，点E，F分别在正方形ABCD的边CD，BC上，且DE=CF，点P在射线BC上(点P不与点F重合).将线段EP绕点E顺时针旋转90得到线段EG，过点E作GD的垂线QH，垂足为点H，交射线BC于点Q．(1)如图①，若点E是CD的中点，点P在线段BF上，则线段BP，QC，EC的数量关系为_______；(2)如图②，若点E不是CD的中点，点P在线段BF上，判断（1）中的结论是否仍然成立．若成立，请写出证明过程；若不成立，请说明理由；(3)若正方形ABCD的边长为6，AB=3DE，CQ=1，请直接写出线段BP的长．12．在菱形ABCD中，∠ABC＝60°，点P是射线BD上一动点，以AP为边向右侧作等边△APE．（1）如图1，当点P在线段BD上时，连接CE，BP与CE的数量关系是________；CE与AD的位置关系是________；（2）当点P在线段BD的延长线上时，（1）中的结论是否还成立？若成立，请予以证明，若不成立，请说明理由、（请结合图2的情况予以证明或说理．）（3）如图3，在（2）的条件下，连接BE，若AB＝2，BE＝，求四边形ADPE的面积．13．在矩形ABCD中，P是线段BC上的一个动点，将△ABP沿直线AP翻折，点B的对应点为E，直线PE与直线AD交于点F．(1)如图①，当点F在AD的延长线上时，求证；(2)若，BC足够长，当点E到直线AD的距离等于3时，求BP的长；(3)若，．当点P、E、D在同一直线上（如图②）时，点P开始向点C运动，到与C重合时停止，则点F运动的路程是______．14．如图，在矩形ABCD中，E是BC上一动点，将△ABE沿AE折叠后得到△AFE，点F在矩形ABCD内部，延长AF交CD于点G，AB＝3，AD＝4．(1)如图1，当∠DAG＝30°时，求BE的长；(2)如图2，当点E是BC的中点时，求线段GC的长；(3)如图3，点E在运动过程中，当△CFE的周长最小时，直接写出BE的长．15．如图1，已知正方形BEFG，点C在BE的延长线上，点A在GB的延长线上，且AB＝BC，过点C作AB的平行线，过点A作BC的平行线，两条平行线相交于点D．(1)证明：四边形ABCD是正方形；(2)当正方形BEFG绕点B顺时针（或逆时针）旋转一定角度，得到图2，使得点G在射线DB上，连接BD和DF，点Q是线段DF的中点，连接CQ和QE，猜想线段CQ和线段QE的关系，并说明理由；(3)将正方形BEFG绕点B旋转一周时，当∠CGB等于45°时，直线AE交CG于点H，探究线段CH、EG、AH的长度关系．培优第二阶——拓展培优练一、解答题1．已知正方形ABCD，∠EAF＝45°，将∠EAF绕顶点A旋转，角的两边始终与直线CD交于点E，与直线BC交于点F，连接EF．（1）如图①，当BF＝DE时，求证：△ABF≌△ADE；（2）若∠EAF旋转到如图②的位置时，求证：∠AFB＝∠AFE；（3）若BC＝4，当边AE经过线段BC的中点时，在AF的右侧作以AF为腰的等腰直角三角形AFP，直接写出点P到直线AB的距离．2．如图，正方形ABCD，将边CD绕点D顺逆时针旋转α（0°＜α＜90°），得到线段DE，连接AE，CE，过点A作AF⊥CE交线段CE的延长线于点F，连接BF．（1）当AE＝AB时，求α的度数；（2）求证：∠AEF＝45°；（3）求证：AE∥FB．3．在四边形ABCD中，∠A＝∠B＝∠C＝∠D＝90°，AB＝CD＝10，BC＝AD＝6，P为射线BC上一点，将△ABP沿直线AP翻折至△AEP的位置，使点B落在点E处．(1)若P为BC上一点．①如图1，当点E落在边CD上时，利用尺规作图，在图1中作出满足条件的点E（不写作法，保留作图痕迹），并直接写出此时CE＝　 　；②如图2，连接CE，若CE∥AP，则BP与BC有何数量关系？请说明理由；(2)如果点P在BC的延长线上，当△PEC为直角三角形时，求PB的长．4．在菱形中，，是对角线上的一点，连接．（1）当在的中垂线上时，把射线绕点顺时针旋转后交于，连接．如图①，若，求的长．（2）在（1）的条件下，连接，把绕点顺时针旋转得到如图②，连接，点为的中点，连接，求的最大值．5．已知四边形ABCD是正方形，AC＝2AO，AD＝2AM，连接BM．(1)如图1，若点M在AD边上，点O在对角线AC上，点E是BM的中点，连接AE．当AB＝4时，求AE的长；(2)如图2，将图1中的△AMO绕点A按顺时针方向旋转，使点O在△ABC的内部，OM与AC相交于点G．连接CO，取CO的中点N，连接MN并延长至点F，使FN＝MN，连接BF．问：线段BM与BF有怎样的关系？请写出具体的解题过程．6．已知：如图①，在矩形中，，垂足是E点F是点E关于的对称点，连接．（1）求和的长；（2）若将沿着射线方向平移，设平移的距离为m（平移距离指点B沿方向所经过的线段长度）当点F分别平移到线段上时，求出相应的m的值; （3）如图②，将绕点B顺时针旋转一个角，记旋转中的为，在旋转过程中，设所在的直线与边交于点P与直线交于点Q是否存在这样的P、Q两点，使为等腰三角形？若存在，直接写出此时的长：若不存在，请说明理由．7．综合与实践如图1，在矩形ABCD中，对角线AC与BD交于点O，将△OBC绕点C顺时针旋转，点B对应点为点E，点O对应点为点F．(1)当点E落在CD的延长线上时，请解答以下两个问题①如图1，若AB＝2a，BC＝2，连接OE，则______（用含a的代数式表示）；②如图2，延长BD交EF于点G，试猜想BG与EF的位置关系并加以证明；(2)如图3，在图1的基础上继续绕点C旋转△OBC，点B对应点为点E，点O对应点为点F，当点E落在BD的延长线上时，已知∠ACE＝90°，求证：四边形CDEF是菱形．8．如图所示，正方形ABCD和正方形AEFG共顶点A，正方形ABCD绕点A顺时针方向旋转，连接DG，BE，BE与AC相交于点H．(1)如图1，在旋转过程中，连接BD，与AC交于点M，当G，A，H，C恰好在同一直线上时，若AE=，AB=2，求线段DG的长：(2)如图2，连接HG，在旋转过程中，BE与DG相交于点O，点K为线段AG中点，连接OK，若∠DGH=2∠ABE，求证：AC=2OK；(3)如图3，BE与DG相交于点O，点K为线段AG上一点连接OK，若AE=3，AK=1，在旋转过程中，直接写出线段OK的最小值．培优第三阶——中考沙场点兵一、解答题1．（2022·山东济南·二模）如图，点E为正方形外一点，，将绕A点逆时针方向旋转得到的延长线交于H点．（1）试判定四边形的形状，并说明理由；（2）已知，求的长．2．（2021·四川德阳·中考真题）如图，点E是矩形ABCD的边BC上一点，将△ABE绕点A逆时针旋转至△AB1E1的位置，此时E、B1、E1三点恰好共线．点M、N分别是AE和AE1的中点，连接MN、NB1．（1）求证：四边形MEB1N是平行四边形；（2）延长EE1交AD于点F，若EB1＝E1F，，判断△AE1F与△CB1E是否全等，并说明理由．3．（2020·贵州贵阳·中考真题）如图，四边形是正方形，点为对角线的中点．（1）问题解决：如图①，连接，分别取，的中点，，连接，则与的数量关系是_____，位置关系是____；（2）问题探究：如图②，是将图①中的绕点按顺时针方向旋转得到的三角形，连接，点，分别为，的中点，连接，．判断的形状，并证明你的结论；（3）拓展延伸：如图③，是将图①中的绕点按逆时针方向旋转得到的三角形，连接，点，分别为，的中点，连接，．若正方形的边长为1，求的面积．4．（2017·山东德州·中考真题）如图1，在矩形纸片ABCD中，AB＝3cm，AD＝5cm，折叠纸片使B点落在边AD上的E处，折痕为PQ，过点E作EFAB交PQ于F，连接BF．（1）求证：四边形BFEP为菱形；（2）当点E在AD边上移动时，折痕的端点P、Q也随之移动；①当点Q与点C重合时（如图2），求菱形BFEP的边长；②若限定P、Q分别在边BA、BC上移动，求出点E在边AD上移动的最大距离．5．（2022·河南·中考真题）综合与实践综合与实践课上，老师让同学们以“矩形的折叠”为主题开展数学活动． 　　 　　(1)操作判断操作一：对折矩形纸片ABCD，使AD与BC重合，得到折痕EF，把纸片展平；操作二：在AD上选一点P，沿BP折叠，使点A落在矩形内部点M处，把纸片展平，连接PM，BM．根据以上操作，当点M在EF上时，写出图1中一个30°的角：______．(2)迁移探究小华将矩形纸片换成正方形纸片，继续探究，过程如下：将正方形纸片ABCD按照（1）中的方式操作，并延长PM交CD于点Q，连接BQ．①如图2，当点M在EF上时，∠MBQ＝______°，∠CBQ＝______°；②改变点P在AD上的位置（点P不与点A，D重合），如图3，判断∠MBQ与∠CBQ的数量关系，并说明理由．(3)拓展应用在（2）的探究中，已知正方形纸片ABCD的边长为8cm，当FQ＝1cm时，直接写出AP的长．6．（2022·海南·中考真题）如图1，矩形中，，点P在边上，且不与点B、C重合，直线与的延长线交于点E．(1)当点P是的中点时，求证：；(2)将沿直线折叠得到，点落在矩形的内部，延长交直线于点F．①证明，并求出在（1）条件下的值；②连接，求周长的最小值；③如图2，交于点H，点G是的中点，当时，请判断与的数量关系，并说明理由．