专题02 空间向量与立体几何（解答题）（人教A版2019）（9月）（原卷版）-2020-2021学年高二《新题速递_数学》

专题02  空间向量与立体几何（解答题）

1．（北京市东城区2019-2020学年高二年级上学期期末教学统一检测数学试题）已知向量，，．

（1）当时，若向量与垂直，求实数和的值；

（2）若向量与向量，共面，求实数的值．

2．（湖北省黄冈市2019-2020学年高二上学期期末数学试题）已知，．

（1）若，求实数的值．

（2）若，求实数的值．

3．（河北省唐山市第一中学2019-2020学年高一下学期期末数学试题）如图所示，菱形ABCD与正三角形BCE的边长均为2，它们所在的平面互相垂直，DF⊥平面ABCD且DF．

（1）求证：EF//平面ABCD；

（2）若∠ABC=∠BCE，求二面角A﹣BF﹣E的余弦值．

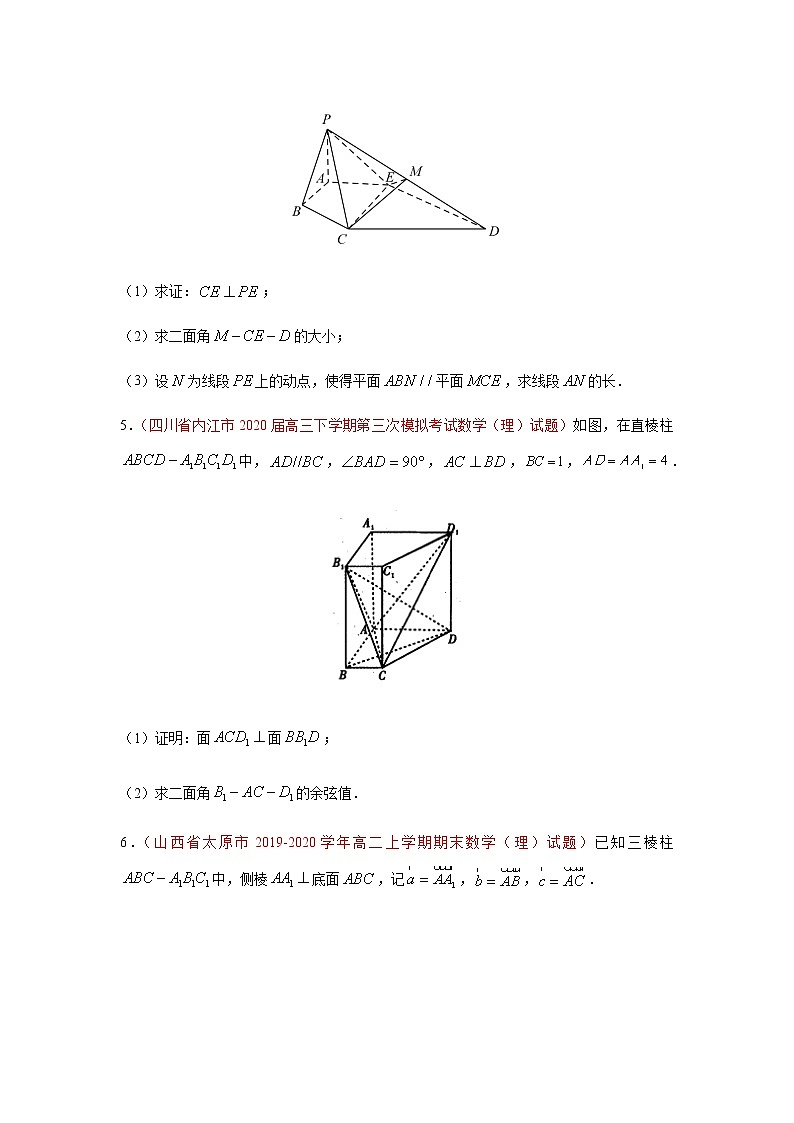
4．（2020届天津市河西区高考一模数学试题）如图所示的几何体中，和均为以为直角顶点的等腰直角三角形，，，，，为的中点．

（1）求证：；

（2）求二面角的大小；

（3）设为线段上的动点，使得平面平面，求线段的长．

5．（四川省内江市2020届高三下学期第三次模拟考试数学（理）试题）如图，在直棱柱中，，，，，．

（1）证明：面面；

（2）求二面角的余弦值．

6．（山西省太原市2019-2020学年高二上学期期末数学（理）试题）已知三棱柱中，侧棱底面，记，，．

（1）用表示；

（2）若，，求证：．

7．（福建省莆田第二十五中学2019-2020学年高二上学期期末考试数学试题）（1）已知向量，分别是直线的方向向量，若，求；

（2）已知向量，，且与互相垂直，求的值．

8．（四川省阆中中学2019-2020学年高二4月月考数学（理）试题）已知空间三点，设．

（1）求和的夹角的余弦值；

（2）若向量互相垂直，求的值．

9．（宁夏育才中学2019-2020学年高二上学期期末考试数学（理）试题）已知，，．

（1）若，求的值；

（2）若，求的值．

10．（广西桂林市龙胜中学2019-2020学年高二开学考试数学（理）试卷）已知，求，，．

11．（广东省茂名地区2019-2020学年高二上学期期末数学试题）已知向量，，．

（1）求

（2）若，求m，n．

（3）求

12．（北京市2020届高考数学预测卷）在四棱锥中，平面，底面四边形为直角梯形，，，，，为中点．

（1）求证：；

（2）求异面直线与所成角的余弦值．

13．（新疆实验中学2019-2020学年高二下学期期末考试数学试题）已知空间中三点，，，设，．

（1）若，且，求向量；

（2）已知向量与互相垂直，求的值；

（3）求的面积．

14．（广西南宁市上林县中学2019-2020学年高一入学考试数学试题）如图所示，在长方体，，，，为棱的中点，分别以，所在的直线为轴、轴、轴，建立空间直角坐标系．

（1）求点的坐标；

（2）求点的坐标．

15．（2020年普通高等学校招生伯乐马押题考试（二）理科数学试题）如图，在四棱锥中，底面，是直角梯形，，，，是的中点．

（1）求证：平面平面；

（2）若二面角的余弦值为，求直线与平面所成角的正弦值．

16．（江西省抚州市2019-2020学年高二上学期期末数学（理）试题）已知三棱锥（如图1）的平面展开图（如图2）中，四边形为边长为的正方形，，均为正三角形，在三棱锥中．

（1）求证：平面平面；

（2）若点在棱上，满足，，点在棱上，且，求得取值范围．

17．（2020届湖南省株洲市第二中学高三下学期4月高考模拟数学试题）如图四棱锥中，底面，是边长为2的等边三角形，且，，点是棱上的动点．

（1）求证：平面平面；

（2）当线段最小时，求直线与平面所成角的正弦值．

18．（四川省叙州区第二中学2019-2020学年高二下学期期末模拟考试数学（理）试题）如图，在棱锥P－中，底面为菱形，且∠DAB＝60°，平面平面，点E为BC中点，点F满足．

（1）求证：平面；

（2）求二面角的余弦值．

19．（四川省宜宾市第四中学2019-2020学年高二下学期期末模拟考试数学（理）试题）如图，在正方体中，点为棱的中点．

（1）证明：平面；

（2）求平面与平面所成二面角的正弦值．

20．（吉林省通钢一中、集安一中、梅河口五中等省示范高中2020届高三（5月份）高考数学（理科）模拟试题）如图，四棱锥的侧棱与四棱锥的侧棱都与底面垂直，，∥，，，，．

（1）证明：∥平面．

（2）求平面平面所成的锐二面角的余弦值．

21．（四川省雅安市2020届高三第一次诊断性考试数学（理）试题）如图，在四棱锥中，底面为正方形，底面，，为线段的中点，若为线段上的动点（不含）．

（1）平面与平面是否互相垂直？如果是，请证明；如果不是，请说明理由；

（2）求二面角的余弦值的取值范围．

22．（浙江省杭州市2020届高三下学期5月高考模拟数学试题）如图，在四棱锥中，底面，底面是直角梯形，，，，E是上的点．

（1）求证：平面平面；

（2）二面角的余弦值为，求直线与平面所成角的正弦值．

23．（湖北省黄石市2019-2020学年高二上学期期末数学试题）如图所示，在四棱柱中，侧棱底面，，，，，为棱的中点．

（1）证明：；

（2）求二面角的正弦值；

（3）设点在线段上，且直线与平面所成角的正弦值是，求线段的长．

24．（安徽省宿州市十三所省重点中学2019-2020学年高二上学期期末考试数学（理）试题）已知平行六面体的底面是边长为1的菱形，且，．

（1）证明：；

（2）求异面直线与夹角的余弦值．

25．（福建省仙游县枫亭中学2019-2020学年高二上学期期末考试数学试题）如图，在棱长为1的正方体中，分别为、、的中点．

（1）求证：平面；

（2）试在棱上找一点，使⊥平面，并证明你的结论．

26．（2020届江苏省南京市中华中学高三下学期阶段考试数学试题）如图，直三棱柱中，底面是等腰直角三角形，，，为的中点，在线段上．

（1）为何值时，平面？

（2）设，求平面与平面所成的锐二面角的余弦值．

27．（陕西省渭南市富平县2019-2020学年高二上学期期末数学（理）试题）如图，在四棱锥中，四边形ABCD为正方形，平面ACD，且，E为PD的中点．

（1）证明：平面平面PAD；

（2）求直线PA与平面AEC所成角的正弦值．

28．（陕西省延安市吴起高级中学2019-2020学年高二下学期第一次质量检测数学（理）试题）已知空间三点，设．

（1）的夹角的余弦值；

（2）若向量互相垂直，求实数的值；

（3）若向量共线，求实数的值．

29．（2020届江苏省连云港市六所四星高中（海州高中、赣榆高中、海头中学、东海高中、新海高中、灌云高中）高三下学期模拟考试数学试题）如图，在四棱锥中，底面是平行四边形，平面，垂足为，在上，且，是的中点．

（1）求异面直线与所成角的余弦值；

（2）若点是棱上一点，且，求的值．

30．（2020届江苏省高三高考全真模拟（九）数学试题）如图，在四棱锥中，底面为直角梯形，，且，平面．

（1）求与平面所成角的正弦值；

（2）棱上是否存在一点满足?若存在，求的长；若不存在，说明理由．

31．（江苏省南京市2020届高三下学期6月第三次模拟考试数学试题）如图，在直三棱柱中ABC—A1B1C1，AB⏊AC，AB＝3，AC＝4，B1C⏊AC1．

（1）求AA1的长；

（2）试判断在侧棱BB1上是否存在点P，使得直线PC与平面AA1C1C所成角和二面角B—A1C—A的大小相等，并说明理由．

32．（四川省德阳市绵竹市南轩中学2019-2020学年高二第一次月考数学（理）试题）如图，在平行六面体中，以顶点为端点的三条棱长都是，且它们彼此的夹角都是，为与的交点．若，，，

（1）用表示；

（2）求对角线的长；

（3）求

33．（陕西省榆林市绥德中学2019-2020学年高二上学期期末理科数学试题）如图，四棱锥的底面为直角梯形，，，，，底面ABCD，E为AB的中点．

求证：（1）∥平面PCB；

（2）平面平面PAC．

34．（福州市2020届高三毕业班第三次质量检查理科数学试题）如图，在多面体中，平面平面，，，，，．

（1）求平面与平面所成二面角的正弦值；

（2）若是棱的中点，求证：对于棱上任意一点，与都不平行．

35．（江苏省南通市如东高级中学2019-2020学年高一下学期6月第二次阶段测试数学试题）平行四边形中，，沿将折起，使二面角是大小为锐角的二面角，设在平面上的射影为．

（1）当为何值时，三棱锥的体积最大？最大值为多少？

（2）当时，求的大小．

36．（新教材精创（教学设计））如图所示，在空间四边形OABC中，OA＝8，AB＝6，AC＝4，BC＝5，∠OAC＝45°，∠OAB＝60°，类比平面向量有关运算，如何求向量与的数量积？并总结求两个向量数量积的方法．

37．（2020届安徽省马鞍山市高三第一次教学质量监测理科数学试题）如图，四边形为矩形，，，以为折痕将折起，使点到达点的位置，且在平面内的射影在边上．

（1）求证：；

（2）求二面角的余弦值．

38．（山西省太原市第五中学2019-2020学年高二11月月考数学（理）试题）如图，以棱长为1的正方体的三条棱所在直线为坐标轴，建立空间直角坐标系，点在线段上，点在线段上．

（1）当，且点关于轴的对称点为点时，求的长度；

（2）当点是面对角线的中点，点在面对角线上运动时，探究的最小值．

39．（江西省吉安县二中2019-2020学年高二上学期期中考试数学试题）已知，．

（1）在轴上求一点，使；

（2）在平面内的点到点与到点等距离，求点的轨迹．

40．（陕西省延安市第一中学2019-2020学年高二下学期6月月考数学（理）试题）如图，以棱长为1的正方体的具有公共顶点的三条棱所在直线为坐标轴，建立空间直角坐标系Oxyz，点P在对角线AB上运动，点Q在棱CD上运动．

（1）当P是AB的中点，且2|CQ|＝|QD|时，求|PQ|的值；

（2）当Q是棱CD的中点时，试求|PQ|的最小值及此时点P的坐标．

41．（天津市新华中学2019-2020学年高三上学期第二次月考数学试题）如图，已知梯形中，，，，四边形为矩形，，平面平面．

（1）求证：平面；

（2）求平面与平面所成二面角的正弦值；

（3）若点在线段上，且直线与平面所成角的正弦值为，求线段的长．

42．（湖南省衡阳市第八中学2020届高三下学期高考适应性考试理科数学试题）如图，三棱柱中，侧面为菱形，．

（1）证明：；

（2）若，，，求二面角的余弦值．

43．（河北省唐山市第一中学2019-2020学年高一下学期期末数学试题）如图，梯形中，，过分别作，，垂足分别，，已知，将梯形沿同侧折起，得空间几何体 ，如图．

1若，证明：平面；

2若，，线段上存在一点，满足与平面所成角的正弦值为，求的长．

44．（湖南省2019-2020学年高二上学期12月联考数学试卷）如图，在棱长为2的正方体中， ， ， ， 分别是棱， ， ， 的中点，点， 分别在棱， 上移动，且．

（1）当时，证明：直线平面；

（2）是否存在，使面与面所成的二面角为直二面角？若存在，求出的值；若不存在，说明理由．

45．（巅峰冲刺2020年高考之二轮专项提升）如图，在四棱锥PABCD中，AP，AB，AD两两垂直，BC∥AD，且AP＝AB＝AD＝4，BC＝2．

（1）求二面角P-CD-A的余弦值；

（2）已知H为线段PC上异于C的点，且DC＝DH，求的值．

46．（北京市第五中学2019-2020学年高二下学期第一次段考数学试题）如图，在三棱柱中，平面，，．

（1）求证：平面；

（2）求异面直线与所成角的大小；

（3）点在线段上，且，点在线段上，若平面，求的值．