【2019年高考二轮课程】数学理科 全国通用版 算法初步与复数 教案

2019年高考二轮复习 算法初步与复数

一、高考回顾

近几年对算法和复数的考查，是各出一道小题。算法题往往考判断条件或输出结果，复数题主要考查运算，这两部分属于稳得分题，难度易。这两个部分复习的关键是：弄清规则，足够量的解题训练。

二、知识清单

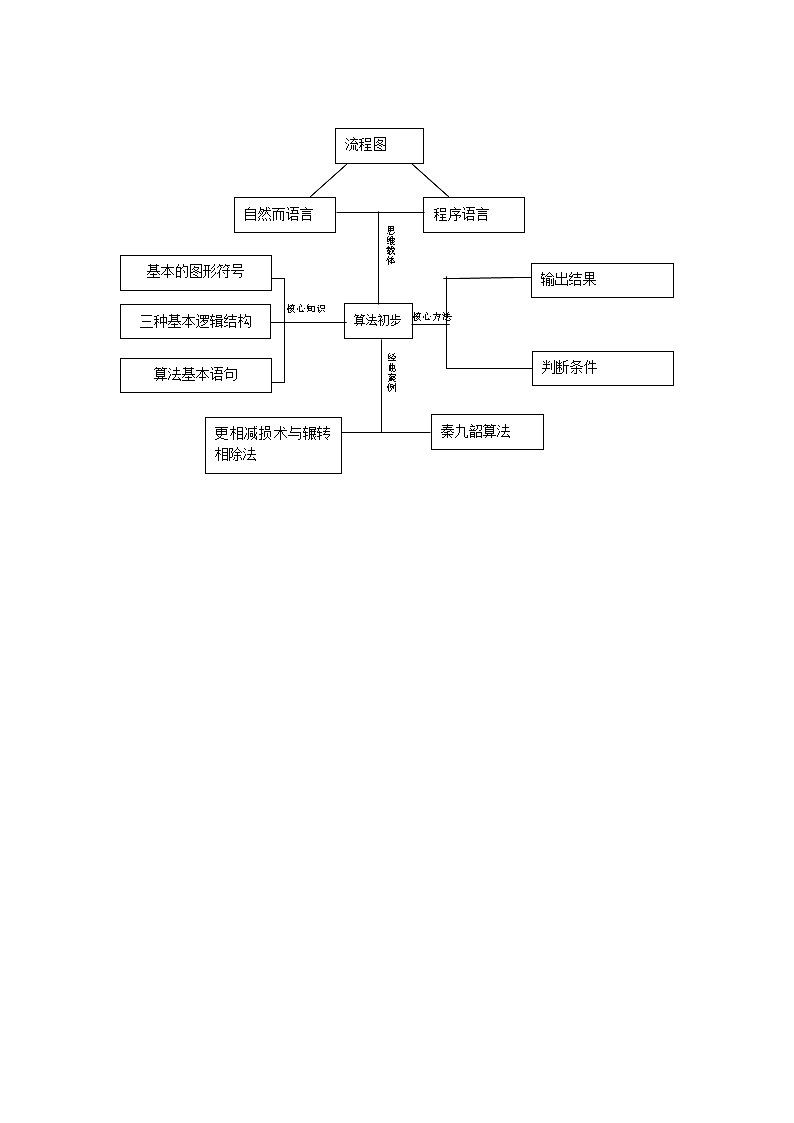
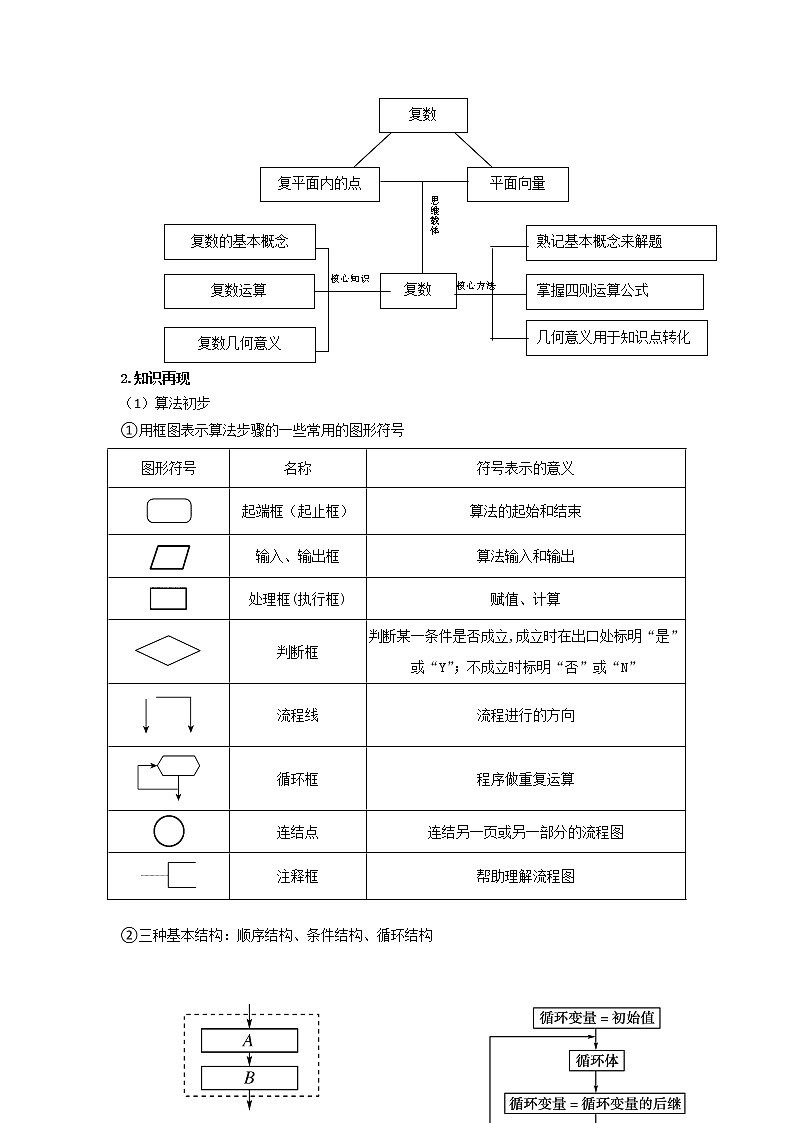
1.思维导图

2.知识再现

（1）算法初步

①用框图表示算法步骤的一些常用的图形符号

②三种基本结构：顺序结构、条件结构、循环结构

③基本算法语句：

1）输入语句、输出语句、赋值语句的格式与功能

①输入语句的一般格式：INPUT“提示内容”；变量

②输出语句的一般格式：PRINT“提示内容”；表达式

③赋值语句的一般格式：变量＝表达式 （“=”有时也用“←”）.

④条件语句：处理条件分支逻辑结构的算法语句.

2）if语句的一般格式:

3）循环语句:

（2）数系的扩充与复数

①复数的概念

1）虚数单位；

2）复数的代数形式；

3）复数的实部、虚部，虚数与纯虚数.

②复数的分类

复数

③相关公式

1）

2）

3）

4）

指两复数实部相同，虚部互为相反数（互为共轭复数）.

④复数运算

1）复数加减法：；

2）复数的乘法：；

3）复数的除法：

（类似于无理数除法的分母有理化虚数除法的分母实数化）

⑤常见的运算规律

1）

2）

3）

4）

5）

6）

7）设是1的立方虚根，则，

⑥复数的几何意义

复平面：用来表示复数的直角坐标系，其中轴叫做复平面的实轴，轴叫做复平面的虚轴.

三、例题精讲

题型一  算法程序框图

例1公元263年左右，我国数学家刘徽发现，当圆内接多边形的边数无限增加时，多边形面积可无限逼近圆的面积，由此创立了割圆术，利用割圆术刘徽得到了圆周率精确到小数点后面两位的近似值，这就是著名的徽率．如图是利用刘徽的割圆术设计的程序框图，则输出的值为 (参考数据:)

【答案】

【解析】模拟执行程序，可得：，

不满足条件 ，

不满足条件 ，

满足条件，退出循环，输出n的值为24．故选：

例2我国古代名著《庄子•天下篇》中有一句名言“一尺之棰，日取其半，万世不竭”，其意思为：一尺的木棍，每天截取一半，永远都截不完．现将该木棍依此规律截取，如图所示的程序框图的功能就是计算截取7天后所剩木棍的长度（单位：尺），则①②③处可分别填入的是（    ）

【答案】

【解析】算法为循环结构，循环7次，每次对长度折半计算，也就是，因此②填，又①填判断语句，需填，③填.故选

题型二 复数基础

例1 若复数满足，则的共轭复数的虚部为（    ）

【答案】

【解析】,，共轭复数,

的共轭复数的虚部,故选

题型三  复数运算

例1复数的共轭复数是（     ）

【答案】

【解析】因为,所以共轭复数是，选

题型四  复数几何意义

例1已知复数，若，则

【答案】

【解析】由复数相等的充分必要条件有，即，则.

四、成果巩固

题型一 算法程序框图

1. 相传黄帝时代，在制定乐律时，用“三分损益”的方法得到不同的竹管，吹出不同的音调．“三分损益”包含“三分损一”和“三分益一”，用现代数学的方法解释如下，“三分损一”是在原来的长度减去一分，即变为原来的三分之二；“三分益一”是在原来的长度增加一分，即变为原来的三分之四，如图的程序是与“三分损益”结合的计算过程，若输入的的值为，输出的的值为  （  ）

【答案】

【解析】因为,结束循环，输出结果，选

2. 日本数学家角谷静夫发现的“猜想”是指：任取一个自然数，如果它是偶数，我们就把它除以，如果它是奇数我们就把它乘再加上，在这样一个变换下，我们就得到了一个新的自然数。如果反复使用这个变换，我们就会得到一串自然数，猜想就是：反复进行上述运算后，最后结果为，现根据此猜想设计一个程序框图如图所示，执行该程序框图输入的，则输出值为（   ）

【答案】

【解析】模拟程序的运行，

可得,不满足条件是奇数，，

不满足条件，执行循环体，不满足是奇数，；

不满足条件，执行循环体，不满足是奇数，,

不满足条件，执行循环体，满足条件是奇数，，

不满足条件，执行循环体，不满足是奇数，；

不满足条件，执行循环体，不满足是奇数，；

不满足条件，执行循环体，不满足是奇数，；

不满足条件，执行循环体，不满足是奇数，，

满足条件，退出循环，输出的值为，故选

3.运行下列框图输出的结果为，则判断框应填入的条件是（     ）

【答案】

【解析】依次运行程序可得：

①，满足条件，继续运行，；

②，满足条件，继续运行，；

③，满足条件，继续运行，；

④，满足条件，继续运行，；

⑤，满足条件，继续运行，；

⑥，不满足条件，输出．结合选项可得选项满足题意．故选

题型二 复数基础

1. 设复数,其中为虚数单位，则的虚部为

【答案】

【解析】,虚部为，

2. 设有下面四个命题，其中的真命题为（   ）

若复数，则        若复数满足，则

若复数满足,则       若复数满足，则

【答案】

【解析】

设,则由,得,因此,从而正确；

设,, 则由,得,从而错误；

设, 则由,得,得，因此错误；

设,, 则由，得得,因此错误；综上选

3. 若复数,且，则的实部为(    )

【答案】

【解析】因为复数,

所以,解得,

可得,

所以，的实部为，故选

题型三 复数运算

1. 若，则( )

【答案】

【解析】，.故选:

2. 欧拉公式(为虚数单位)是由瑞士著名数学家欧拉发现的，它将指数函数的定义域扩大到复数，建立了三角函数和指数函数的关系，它在复变函数论里非常重要，被誉为“数学中的天桥”。根据欧拉公式可知，表示的复数位于复平面中的

第一象限        第二象限        第三象限        第四象限

【答案】

【解析】由欧拉公式(为虚数单位)可得：

表示的复数对应的点为，此点位于第二象限,故选

3. 若实数满足（为虚数单位），则

【答案】

【解析】由题得

题型四 复数几何意义

1. 若复数（为虚数单位）,的共轭复数在复平面内对应的点在（   ）

第一象限        第二象限        第三象限        第四象限

【答案】

【解析】复数，则的共轭复数在复平面内对应的点在第四象限．

2. 已知复数满足,则等于(  )

【答案】

【解析】由题可知表示平行四边形的相邻两边,表示平行四边形的一条对角线则由题意为等边三角形,则在三角形中,由余弦定理可得,将,代入可得.故选

3. 若复数为纯虚数,则

【答案】

【解析】由复数的运算法则有：,

复数为纯虚数,则

即.

五、课堂小结

1、     算法初步

主要题型：程序框图的输出或条件补充

(1)程序框图输出结果题型：

在给出程序框图求解输出结果的试题中只要按照程序框图规定的运算方法逐次计算，直到达到输出条件即可.

(2)解答不全程序框图中的条件的问题的策略：

①先假设参数的判断条件满足或不满足；

②运行循环结构，一直到运行结果与题目要求的输出结果相同为止；

③根据此时各个变量的值，补全程序框图中欠缺的条件．

2、复数相关概念与运算的技巧

(1)解决与复数的基本概念和性质有关的问题时，应注意复数和实数的区别与联系，把复数问题实数化是解决复数问题的关键．

(2)复数相等问题一般通过实部与虚部对应相等列出方程或方程组求解．

(3)复数的代数运算的基本方法是运用运算法则，但可以通过对代数式结构特征的分析，灵活运用i的幂的性质、运算法则来优化运算过程．

(4)复数的几何意义、模长等直接通过运算即可