

2021年中考(通用版)数学一轮复习:圆 含答案 试卷
展开基础小卷测(17) 圆
满分100分
姓名:___________班级:___________学号:___________
题号 | 一 | 二 | 三 | 总分 |
得分 |
|
|
|
|
一.选择题(共8小题,满分32分,每小题4分)
1.⊙O的半径为5cm,点A到圆心O的距离OA=3cm,则点A与圆O的位置关系为( )
A.点A在圆上 B.点A在圆内 C.点A在圆外 D.无法确定
2.如图,点A、B、C在⊙O上,若∠BOC=70°,则∠A的度数为( )
A.35° B.40° C.55° D.70°
3.如图,四边形ABCD内接于⊙O,若∠B=108°,则∠D的大小为( )
A.54° B.62° C.72° D.82°
4.一个圆锥的底面半径是4cm,其侧面展开图的圆心角是120°,则圆锥的母线长是( )
A.8cm B.12cm C.16cm D.24cm
5.如图,⊙O的直径CD=20,AB是⊙O的弦,AB⊥CD,垂足为M,OM:OC=3:5,则AB的长为( )
A.8 B.12 C.16 D.2
6.如图,扇形的半径为6cm,圆心角为120°,则该扇形的面积为( )
A.6πcm2 B.9πcm2 C.12πcm2 D.18πcm2
7.如图,Rt△ABC中,∠C=90°,AB=5,cosA=,以点B为圆心,r为半径作⊙B,当r=3时,⊙B与AC的位置关系是( )
A.相离 B.相切 C.相交 D.无法确定
8.如图,AB是⊙O的直径,CD是弦,点C,D在直径AB的两侧.若∠AOC:∠AOD:∠DOB=2:7:11,CD=4,则的长为( )
A.2π B.4π C. D.π
二.填空题(共6小题,满分30分,每小题5分)
9.(5分)如图,在⊙O中,点A在上,∠BOC=100°.则∠BAC= °.
10.(5分)如果圆锥的侧面展开图的扇形半径是6,弧长是4π,那么这个扇形的圆心角为 .
11.(5分)如图,小丽荡秋千,秋千链子的长OA为2.5米,秋千向两边摆动的角度相同,摆动的水平距离AB为3米,则秋千摆至最高位置时与最低价位置时的高度之差(即CD)为 米.
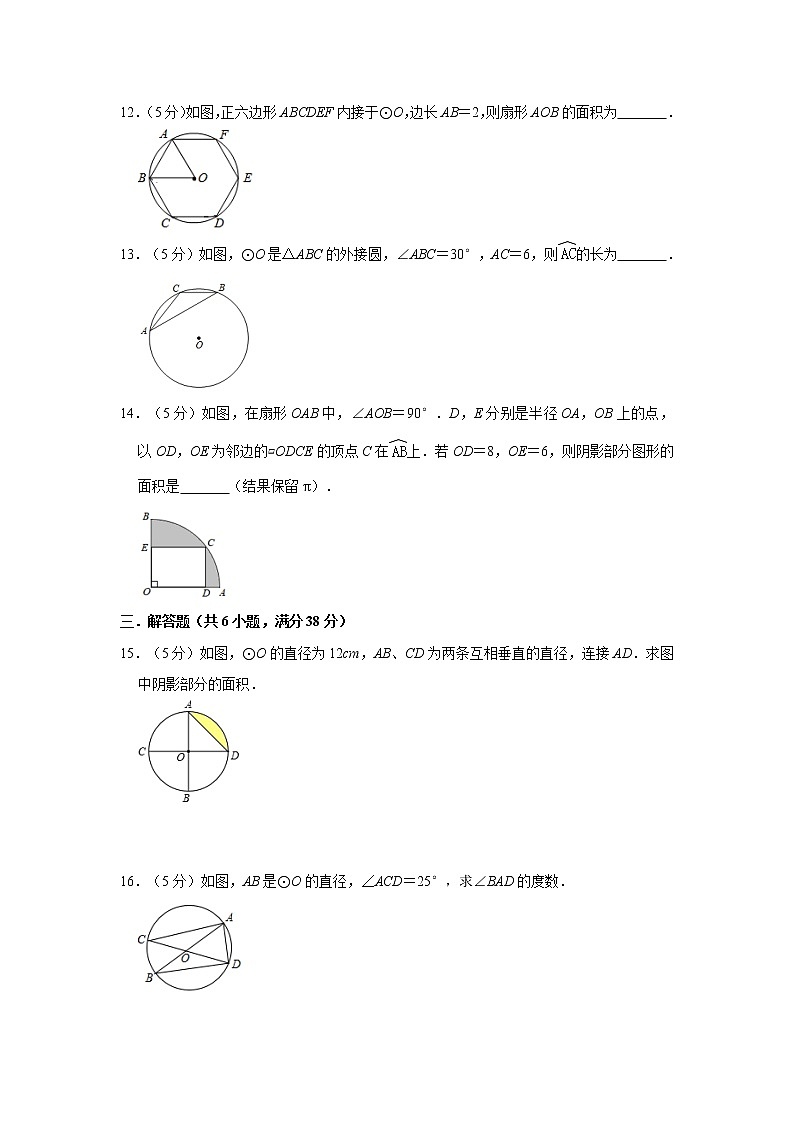
12.(5分)如图,正六边形ABCDEF内接于⊙O,边长AB=2,则扇形AOB的面积为 .
13.(5分)如图,⊙O是△ABC的外接圆,∠ABC=30°,AC=6,则的长为 .
14.(5分)如图,在扇形OAB中,∠AOB=90°.D,E分别是半径OA,OB上的点,以OD,OE为邻边的▱ODCE的顶点C在上.若OD=8,OE=6,则阴影部分图形的面积是 (结果保留π).
三.解答题(共6小题,满分38分)
15.(5分)如图,⊙O的直径为12cm,AB、CD为两条互相垂直的直径,连接AD.求图中阴影部分的面积.
16.(5分)如图,AB是⊙O的直径,∠ACD=25°,求∠BAD的度数.
17.(6分)如图所示,该小组发现8米高旗杆DE的影子EF落在了包含一圆弧型小桥在内的路上,于是他们开展了测算小桥所在圆的半径的活动.小刚身高1.6米,测得其影长为2.4米,同时测得EG的长为3米,HF的长为1米,测得拱高(弧GH的中点到弦GH的距离,即MN的长)为2米,求小桥所在圆的半径.
18.(6分)如图,⊙O的直径AB的长为10,弦AC的长为5,∠ACB的平分线交⊙O于点D.
(1)求的长.
(2)求弦BD的长.
19.(8分)如图,在Rt△AOB中,∠AOB=90°,OA=OB,点C是AB的中点,以OC为半径作⊙O.
(1)求证:AB是⊙O的切线;
(2)若OC=2,求OA的长.
20.(8分)如图,在Rt△ABC中,∠C=90°,点O在AC上,以OA为半径的半圆O交AB于点D,交AC于点E,过点D作半圆O的切线DF,交BC于点F.
(1)求证:BF=DF;
(2)若AC=4,BC=3,CF=1,求半圆O的半径长.
参考答案
一.选择题(共8小题,满分32分,每小题4分)
1.【解答】解:∵⊙O的半径为5cm,点A到圆心O的距离为3cm,
即点A到圆心O的距离小于圆的半径,
∴点A在⊙O内.
故选:B.
2.【解答】解:∵如图,∠BOC=70°,
∴∠A=∠BOC=35°.
故选:A.
3.【解答】解:∵四边形ABCD内接于⊙O,∠B=108°,
∴∠D=180°﹣∠B=180°﹣108°=72°,
故选:C.
4.【解答】解:圆锥的底面周长为2π×4=8πcm,即为展开图扇形的弧长,
由弧长公式得=8π,
解得,R=12,即圆锥的母线长为12cm.
故选:B.
5.【解答】解:连接OA,
∵⊙O的直径CD=20,OM:OC=3:5,
∴OC=10,OM=6,
∵AB⊥CD,
∴AM===8,
∴AB=2AM=16.
故选:C.
6.【解答】解:由题意得,n=120°,R=6cm,
故=12π.
故选:C.
7.【解答】解:∵Rt△ABC中,∠C=90°,AB=5,cosA=,
∴==,
∴AC=4,
∴BC==3,
∵r=3,
∴BC=r=3,
∴⊙B与AC的位置关系是相切,
故选:B.
8.【解答】解:∵∠AOC:∠AOD:∠DOB=2:7:11,∠AOD+∠DOB=180°,
∴∠AOD=×180°=70°,∠DOB=110°,∠COA=20°,
∴∠COD=∠COA+∠AOD=90°,
∵OD=OC,CD=4,
∴2OD2=42,
∴OD=2,
∴的长是==,
故选:D.
二.填空题(共6小题,满分30分,每小题5分)
9.【解答】解:如图,在优弧BC上取一点D,且异于B,C,连接BD,CD,
则四边形ABDC是⊙O的内接四边形,
∴∠D+∠BAC=180°.
∵∠BOC=100°,
∴∠D=50°,
∴∠BAC=180°﹣50°=130°,
故答案为:130.
10.【解答】解:设这个扇形的圆心角为n°,
则=4π,
解得,n=120,
故答案为:120°.
11.【解答】解:∵点C为弧AB的中点,O为圆心
由垂径定理知:AB⊥OC,AD=BD=AB=1.5米,
在Rt△OAD中,根据勾股定理,OD==2(米),
∴CD=OC﹣OD=2.5﹣2=0.5(米);
故答案为0.5.
12.【解答】解:∵正六边形ABCDEF内接于⊙O,
∴∠AOB=60°,
∵OA=OB,
∴△AOB是等边三角形,
∴OA=OB=AB=2,
∴扇形AOB的面积==,
故答案为:.
13.【解答】解:连接OC,OA.
∵∠AOC=2∠ABC,∠ABC=30°,
∴∠AOC=60°,
∵OA=OC,
∴△AOC是等边三角形,
∴OA=OC=AC=6,
∴的长==2π,
故答案为2π.
14.【解答】解:连接OC,
∵∠AOB=90°,四边形ODCE是平行四边形,
∴▱ODCE是矩形,
∴∠ODC=90°.
∵OD=8,OE=6,
∴OC=10,
∴阴影部分图形的面积=﹣8×6=25π﹣48.
故答案为:25π﹣48.
三.解答题(共6小题,满分38分)
15.【解答】解:阴影部分的面积=﹣6×6÷2=9π﹣18(cm2).
16.【解答】解:∵AB为⊙O直径
∴∠ADB=90°
∵相同的弧所对应的圆周角相等,且∠ACD=25°
∴∠B=25°
∴∠BAD=90°﹣∠B=65°.
17.【解答】解:∵小刚身高1.6米,测得其影长为2.4米,
∴8米高旗杆DE的影子为:12m,
∵测得EG的长为3米,HF的长为1米,
∴GH=12﹣3﹣1=8(m),
∴GM=MH=4m.
如图,设小桥的圆心为O,连接OM、OG.
设小桥所在圆的半径为r,
∵MN=2m,
∴OM=(r﹣2)m.
在Rt△OGM中,由勾股定理得:
∴OG2=OM2+42,
∴r2=(r﹣2)2+16,
解得:r=5,
答:小桥所在圆的半径为5m.
18.【解答】解:(1)如图,连接OC,OD,,
∵AB是⊙O的直径,
∴∠ACB=∠ADB=90°,
在Rt△ABC中,
∵,
∴∠BAC=60°,
∴∠BOC=2∠BAC=2×60°=120°,
∴的长=.
(2)∵CD平分∠ACB,
∴∠ACD=∠BCD,
∴∠AOD=∠BOD,
∴AD=BD,
∴∠ABD=∠BAD=45°,
在Rt△ABD中,
BD=AB×sin45°=10×.
19.【解答】(1)证明:∵OA=OB,点C是AB的中点,
∴OC⊥AB,
∵OC为⊙O的半径,
∴AB是⊙O的切线;
(2)∵△AOB是等腰直角三角形,点C是AB的中点,
∴OC⊥AB,AB=2OC=4,
∵OA2=,
∴OA==2.
20.【解答】解:(1)连接OD,如图1,
∵过点D作半圆O的切线DF,交BC于点F,
∴∠ODF=90°,
∴∠ADO+∠BDF=90°,
∵OA=OD,
∴∠OAD=∠ODA,
∴∠OAD+∠BDF=90°,
∵∠C=90°,
∴∠OAD+∠B=90°,
∴∠B=∠BDF,
∴BF=DF;
(2)连接OF,OD,如图2,
设圆的半径为r,则OD=OE=r,
∵AC=4,BC=3,CF=1,
∴OC=4﹣r,DF=BF=3﹣1=2,
∵OD2+DF2=OF2=OC2+CF2,
∴r2+22=(4﹣r)2+12,
∴.
故圆的半径为.








