




- 21.2.3二次函数的图象和性质(第三课时)课件 课件 10 次下载
- 21.2.5二次函数的图象和性质(第五课时)课件 课件 11 次下载
- 21.4.1二次函数的应用 第1课时 课件 课件 14 次下载
- 21.4.2二次函数的应用 第2课时 课件 课件 11 次下载
- 21.5.1 反比例函数 第1课时 课件 课件 11 次下载
沪科版九年级上册21.3 二次函数与一元二次方程一等奖ppt课件
展开1、一元二次方程x2-2x-3=0的根为:____________2、一元二次方程ax2+bx+c=0(a≠0)的根的判别式△ = __ 。当△﹥0方程根的情况是: _________________ ;当△=0时,方程 __________________ ; 当△﹤0时,方程 ____________ 。3、二次函数y=ax2+bx+c(a、b、c是常数,且a≠0)图像是一条 ______ ,它与x轴的交点有几种可能的情况?
4.一次函数与一元一次方程的关系:
一次函数y=kx+b的图像与x轴交点的横坐标就是一次方程kx+b=0的解。
那么,二次函数与一元二次方程有什么关系呢?
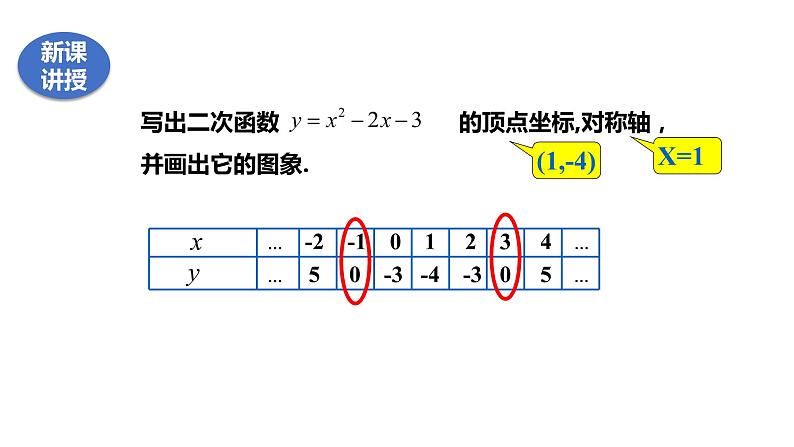
… -2 -1 0 1 2 3 4 …
… 5 0 -3 -4 -3 0 5 …
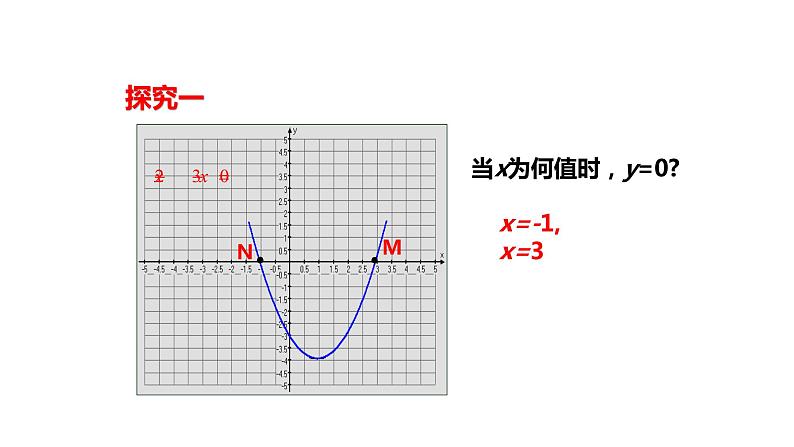
当x为何值时,y=0?
x=-1, x=3
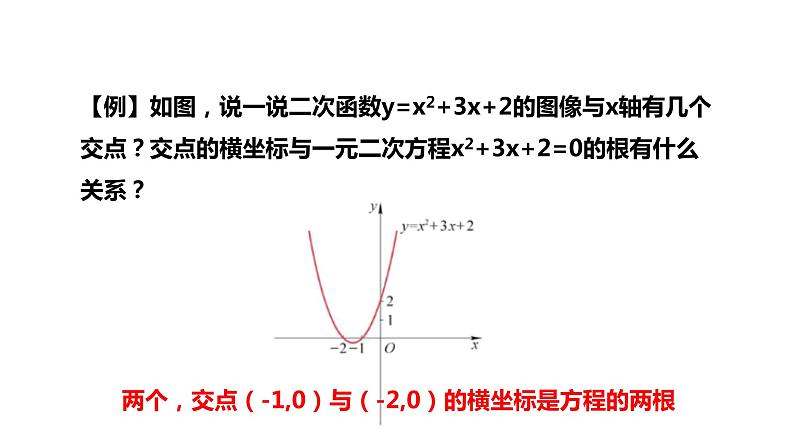
【例】如图,说一说二次函数y=x2+3x+2的图像与x轴有几个交点?交点的横坐标与一元二次方程x2+3x+2=0的根有什么关系?
两个,交点(-1,0)与(-2,0)的横坐标是方程的两根
一般地,如果二次函数y=ax2+bx+c 的图象与x轴有两个公共点(x1,0)、(x2,0 )那么一元二次方程ax2+bx+c=0 有两个不相等的实数根x=x1、x=x2 ,反之亦成立.
所以,函数 的图象与 x 轴的交点坐标为(-3,0)和(2,0).
观察二次函数y=x²-6x+9的图象和二次函数y=x²-2x+3的图象,分别说出一元二次方程x²-6x+9=0和x²-2x+3=0的根的情况.
二次函数y=ax2+bx+c的图象与x轴交点的坐标与一元二次方程ax2+bx+c=0根的关系?
例:用图象法求一元二次方程x²+2x-1= 0 的近似解(精确到0.1)。
解:画出函数图像,如图。由图像可知,方程有两个实数根,一个在-3和-2之间,另一个在0和1之间。
方程x²+2x-1= 0的近似解还可以这样求:分别画出函数y=x2和y=-2x+1的图像,它们交点A,B的横坐标就是方程x²+2x-1= 0的根。
变式:利用二次函数的图象求一元二次方程x²+x-1= 0 的近似解。
自己进行画图,得到近似解为x1 ≈ 0.6,x2 ≈-1.6
通过这节课的学习活动,你有哪些收获?
1.如图,在平面直角坐标系中,抛物线y=(x-h)2与x轴只有一个交点M,与平行于x轴的直线l交于点A、B,若AB=4,则点M到直线l的距离为( )A.2B.3C.4D.5
2.小明研究二次函数y=-x2+2mx-m2+1(m为常数)性质时有如下结论: ①该二次函数图象顶点始终在平行于x轴的直线上; ②该二次函数图象的顶点与x轴的两个交点构成等腰直角三角形; ③当-1<x<2时,y随x的增大而增大,则m的值范围为m≥2; ④点A(x1y1)与点B(x2,y2)在函数图象上,若x1<x2,x1+x2>2m,则y1>y2; 其中正确结论的个数为( )A.1 B.2 C.3 D.4
沪科版九年级上册21.3 二次函数与一元二次方程教学演示课件ppt: 这是一份沪科版九年级上册21.3 二次函数与一元二次方程教学演示课件ppt,共20页。PPT课件主要包含了旧知回顾,x=4,x=-2,问题1,问题2,观察图象完成下表,有两个交点,有两个不相等的实数根,b2-4ac>0,有一个交点等内容,欢迎下载使用。
数学九年级上册21.3 二次函数与一元二次方程精品作业课件ppt: 这是一份数学九年级上册21.3 二次函数与一元二次方程精品作业课件ppt,共1页。
沪科版九年级上册第21章 二次函数与反比例函数21.3 二次函数与一元二次方程说课ppt课件: 这是一份沪科版九年级上册第21章 二次函数与反比例函数21.3 二次函数与一元二次方程说课ppt课件,共13页。PPT课件主要包含了x-1x3,探究一,解当y0时,探究二,有两个交点,有两个不相等的实数根,b2-4ac0,有一个交点,有两个相等的实数根,没有交点等内容,欢迎下载使用。













