- 第2章第4节 科学测量:做直线运动物体的瞬时速度 学案 0 次下载
- 第2章第5节 自由落体运动 讲义 学案 0 次下载
- 第2章习题课 匀变速直线运动的平均速度公式和位移差公式的应用 学案 0 次下载
- 第2章章末过关检测(二) 试卷 0 次下载
- 第3章第1节 重力与重心 讲义 学案 0 次下载
高中物理鲁科版 (2019)必修 第一册第2章 匀变速直线运动本章综合与测试综合训练题
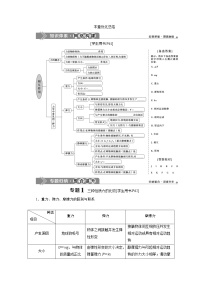
展开本章优化总结
[学生用书P41]
求匀变速直线运动的常用方法[学生用书P42]
由于运动学部分的公式较多,并且各公式之间又相互联系,因此本章中的一些题目常可一题多解.在解题时要开阔思路,联想比较,筛选出最便捷的解题方案,从而简化解题过程.本章常用的解题方法及规律特点见下表:
续 表
物体以一定的初速度从底端A点冲上固定的光滑斜面,到达斜面最高点C时速度恰好为零,如图所示.已知物体运动到斜面长度eq \f(3,4)处的B点时,所用时间为t,求物体从B运动到C所用的时间.
[解析] 法一:一般公式法
设物体初速度为v0,加速度大小为a,方向沿斜面向下,从A到C用时t1,已知从A到B用时t,则由运动速度和位移公式得:sAB=v0t-eq \f(1,2)at2,
sAC=v0t1-eq \f(1,2)ateq \\al(2,1),
且sAB=eq \f(3,4)sAC
又vB=v0-at,vC=vB-a(t1-t)=0
联立求解可得:t1=2teq \b\lc\(\rc\)(\a\vs4\al\c1(另一解t1=\f(2,3)t不合理,舍去))
故物体从B运动到C所用的时间tBC=t1-t=t.
法二:逆向思维法
物体向上匀减速冲上斜面,相当于向下匀加速滑下斜面,有sBC=eq \f(1,2)ateq \\al(2,BC),sAC=eq \f(a(t+tBC)2,2),且sBC=eq \f(sAC,4)
解得tBC=t.
法三:比例法
对于初速度为零的匀变速直线运动,在连续相等的时间内通过的位移之比为
s1∶s2∶s3∶…=1∶3∶5∶…
现在sBC∶sAB=1∶3,通过sAB的时间为t,
故通过sBC的时间tBC=t.
法四:中间时刻速度法
利用推论:中间时刻的瞬时速度等于这段时间内的平均速度,有eq \x\t(v)AC=eq \f(1,2)(vt+v0)=eq \f(v0,2)
又veq \\al(2,0)=2asAC,veq \\al(2,B)=2asBC,sBC=eq \f(1,4)sAC
由以上各式解得:vB=eq \f(v0,2)=vAC
可以看出vB正好等于AC段的平均速度,因此B点是中间时刻,即tBC=t.
法五:图像法
利用相似三角形面积之比等于对应边二次方比的方法,作出v-t图像,如图所示.
eq \f(S△AOC,S△BDC)=eq \f(CO2,CD2)
且S△AOC=4S△BDC,OD=t,OC=t+tBC
所以eq \f(4,1)=eq \f((t+tBC)2,teq \\al(2,BC)),解得tBC=t.
[答案] t
一个做匀加速直线运动的物体,在前4 s内经过的位移为24 m,在第2个4 s内经过的位移是60 m,求这个物体的加速度和初速度各是多少?
解析:由公式Δs=aT 2,得a=eq \f(Δs,T2)=eq \f(60-24,42) m/s2=2.25 m/s2,
根据v4=eq \f(24+60,8) m/s=v0+4a,
得v0=1.5 m/s.
答案:2.25 m/s2 1.5 m/s
运动图像的意义及应用[学生用书P43]
续 表
(多选)(2018·高考全国卷 Ⅱ )甲、乙两汽车在同一条平直公路上同向运动,其速度-时间图像分别如图中甲、乙两条曲线所示.已知两车在t2时刻并排行驶.下列说法正确的是( )
A.两车在t1时刻也并排行驶
B.在t1时刻甲车在后,乙车在前
C.甲车的加速度大小先增大后减小
D.乙车的加速度大小先减小后增大
[解析] 本题可巧用逆向思维分析,两车在t2时刻并排行驶,根据题图分析可知在t1~t2时间内甲车运动的位移大于乙车运动的位移,所以在t1时刻甲车在后,乙车在前,B正确,A错误;依据v-t图像斜率表示加速度分析出C错误,D正确.
[答案] BD
【达标练习】
1.(多选)(2018·高考全国卷 Ⅲ )
甲、乙两车在同一平直公路上同向运动,甲做匀加速直线运动,乙做匀速直线运动.甲、乙两车的位置x随时间t的变化如图所示.下列说法正确的是( )
A.在t1时刻两车速度相等
B.从0到t1时间内,两车走过的路程相等
C.从t1到t2时间内,两车走过的路程相等
D.在t1到t2时间内的某时刻,两车速度相等
解析:选CD.x-t图像某点的切线斜率表示瞬时速度,A错误;前t1时间内,由于甲、乙的出发点不同,故路程不同,B错误;t1~t2时间内,甲、乙的位移和路程都相等,大小都为x2-x1,C正确;t1~t2时间内,甲的x-t图像在某一点的切线与乙的x-t图像平行,此时刻两车速度相等,D正确.
2.(多选)物体甲的s-t图像和物体乙的v-t图像如所示,则这两物体的运动情况是( )
A.甲在整个t=6 s时间内运动方向一直不变,它通过的总位移大小为4 m
B.甲在整个t=6 s时间内有往返运动,它通过的总位移为零
C.乙在整个t=6 s时间内有往返运动,它通过的总位移为零
D.乙在整个t=6 s时间内运动方向一直不变,它通过的总位移大小为4 m
解析:选AC.甲图为s-t图像,图像的斜率表示速度,甲的斜率一直为正,故甲的运动方向不变,通过的总位移大小为4 m,选项A正确,B错误;乙图为v-t图像,速度有正有负,表示有往返运动.v-t图像中图线与时间轴所围面积表示位移的大小,在整个t=6 s时间内乙通过的总位移为零,选项C正确,D错误.
追及、相遇问题[学生用书P43]
1.追及问题
(1)追及的特点:两个物体在同一时刻处在同一位置.
(2)追及问题满足的两个关系
①时间关系:从后面的物体追赶开始,到追上前面的物体时,两物体经历的时间相等.
②位移关系:s2=s0+s1
其中s0为开始追赶时两物体之间的距离,s1表示前面被追物体的位移,s2表示后面追赶物体的位移.
(3)临界条件:当两个物体的速度相等时,可能出现恰好追上、恰好避免相撞、相距最远、相距最近等情况,即出现上述四种情况的临界条件为v1=v2.
2.相遇问题
相向运动的物体,各自发生的位移的绝对值之和等于开始时两物体间的距离时即相遇.在避碰问题中,关键是把握临界状态,避碰问题的临界状态还是反映在速度相等这一关键点上,即两个运动物体具有相同的位置坐标时,两者的相对速度为零.
3.分析追及问题的一般方法
(1)一般解题思路
(2)解题技巧
①抓住三个关系,即“位移关系”“时间关系”“速度关系”;用好示意图.
②寻找隐含的临界条件,如“刚好”“恰好”等关键词往往是解题的突破点.
③若被追赶的物体做减速运动,要判断它何时停下.
一辆汽车以3 m/s2的加速度开始启动的瞬间,一辆以6 m/s的速度做匀速直线运动的自行车恰好从汽车旁边经过.求:
(1)汽车追上自行车前二者相距的最远距离为多少?
(2)汽车经多长时间追上自行车?追上自行车时瞬时速度多大?
[解析] 法一:物理分析的方法
(1)汽车“追赶”自行车,它们的间距先增后减,当二者速度相同时,间距最大.设二者速度相同,均为6 m/s,所经过的时间为t1,则at1=v自,t1=eq \f(v自,a)=eq \f(6,3) s=2 s,最大间距Δs=v自t1-eq \f(1,2)ateq \\al(2,1)=eq \b\lc\(\rc\)(\a\vs4\al\c1(6×2-\f(1,2)×3×22)) m=6 m.
(2)追上时间为t2,则v自t2=eq \f(1,2)ateq \\al(2,2),即6t2=eq \f(1,2)×3×teq \\al(2,2),t2=4 s,此时汽车速度v2=at2=12 m/s.
法二:数学分析的方法
(1)经时间t,二者间距为Δs=v自t-eq \f(1,2)at2=6t-eq \f(1,2)×3×t2=-eq \f(3,2)(t-2)2+6,当t=2 s时,间距最大,Δsm=6 m.
(2)追上时解法同法一.
法三:图像法
根据题意,从汽车启动瞬间计时,分别作出汽车与自行车的v-t图像,如图所示.
(1)由图像可知,2 s前自行车与汽车间距增大,2 s后汽车“追赶”自行车,它们的间距减小,因此t=2 s时二者间距最大,最大距离与三角形OAB面积数值相等,即
Δsm=6×2×eq \f(1,2) m=6 m.
(2)当所画阴影三角形OAB与三角形CDB面积相等时汽车追上自行车,由两三角形全等可知,在t=4 s时汽车追上自行车,由图像知此时汽车速度为12 m/s.
[答案] (1)6 m (2)4 s 12 m/s
eq \a\vs4\al()
解追及、相遇问题的一般思路
(1)根据对两物体运动过程的分析,画出物体运动的示意图.
(2)根据两物体的运动性质,分别列出两个物体的位移方程,注意要将两物体运动时间的关系反映在方程中.
(3)由运动示意图找出两物体位移间的关联方程,这是关键.
(4)联立方程求解,并对结果进行简单分析.
为打击贩毒,我边防民警在各交通要道上布下天罗地网.某日,一辆藏毒汽车高速驶进某检查站,警方示意停车,毒贩见势不妙,高速闯卡.闯卡后,此车在平直公路上可视为做匀速直线运动,其位移可由公式s1=50t来描述.藏毒车闯卡同时,原来停于卡口边的大功率警车立即启动追赶,警车从启动到追上毒贩的运动可看作匀加速直线运动,其位移可由公式s2=2t2来描述.本题位移单位均为m,时间单位均为s,则由以上信息可求:
(1)藏毒车逃跑时的速度是多大?警车追赶藏毒车时的加速度为多大?
(2)在追赶过程中,经多长时间警车与藏毒车的距离最远,最远距离为多少?
(3)警车经多长时间追上藏毒车,追上时已距离检查站多远?
解析:(1)藏毒车逃跑时的速度v0=50 m/s,
警车追赶藏毒车时的加速度a=4 m/s2.
(2)当警车速度v与藏毒车速度v0相等时距离最远
即v=at1,得t1=12.5 s
此过程藏毒车位移
s1=50t1=50×12.5 m=625 m
警车位移
s2=2teq \\al(2,1)=2×12.52 m=312.5 m
最远距离
Δs=s1-s2=625 m-312.5 m=312.5 m.
(3)警车追上藏毒车时位移相同
即50t2=2teq \\al(2,2),得t2=25 s
此时与检查站的距离s=50t2=50×25 m=1 250 m.
答案:(1)50 m/s 4 m/s2 (2)12.5 s 312.5 m
(3)25 s 1 250 m
纸带的应用问题[学生用书P45]
1.由纸带判断物体的运动性质
在纸带上测出各个连续相等的时间T内的位移分别是s1、s2、…、sn:
(1)如果s1=s2=…=sn,则物体做匀速直线运动;
(2)如果s2-s1=s3-s2=…=sn-sn-1≠0,即在连续相等时间内的位移差相等,则物体做匀变速直线运动;如果不相等,则物体做变加速直线运动.
2.由纸带计算物体的速度
如果物体做匀变速直线运动,s1、s2、…、sn为其在连续相等时间内的位移,T为相等时间间隔值,则纸带上某点对应的瞬时速度等于以这个点为中间时刻的位移内的平均速度,即vn=eq \f(sn+sn+1,2T).
3.由纸带计算物体运动的加速度
(1)v-t图像法:利用求得的多个速度值及对应时间描绘出v-t图像,则v-t图线斜率即为物体运动的加速度.
(2)逐差法:如图所示的纸带,按时间顺序取0、1、2、3、4、5、6七个计数点,测量相邻两点之间的距离分别是s1、s2、s3、s4、s5、s6,T为计数点间的时间,
由Δs=aT2可得
s4-s1=3a1T2,s5-s2=3a2T2,s6-s3=3a3T2,则物体运动的加速度
a=eq \f(1,3)(a1+a2+a3)
=eq \f((s4+s5+s6)-(s1+s2+s3),9T2)
同理可得若有4段位移
a=eq \f((s3+s4)-(s1+s2),4T2).
如图所示是某同学测量匀变速直线运动的加速度时,从若干纸带中选中的一条纸带的一部分,他每隔4个点取一个计数点,图上注明了他对各个计数点间距离的测量结果(单位:cm).
(1)为了验证小车的运动是匀变速直线运动,请进行下列计算,填入表内(单位:cm).
各位移差与平均值最多相差________cm,由此可得出结论:在________范围内小车在________的位移之差相等,所以小车的运动是________________________________________________________________________.
(2)小车的加速度为________m/s2.
[解析] (1)由题中数据可求各位移差依次为1.60 cm、1.55 cm、1.62 cm、1.53 cm、1.61 cm,其平均值Δs≈1.58 cm,各位移与平均值最多相差0.05 cm,所以在误差允许范围内,小车在相邻相等时间内位移之差相等,因此小车做匀加速直线运动.
(2)由“逐差法”求加速度:
a=eq \f((s6+s5+s4)-(s3+s2+s1),9T2)
=eq \f((10.71+9.10+7.57)-(5.95+4.40+2.80),9×(0.1)2)×10-2 m/s2≈1.58 m/s2.
[答案] (1)1.60 1.55 1.62 1.53 1.61 1.58 0.05 误差允许 相邻相等的时间内 匀加速直线运动
(2)1.58
(2019·温州高一检测)如图所示是用小车拖动纸带,用打点计时器测定匀加速运动的加速度时打出的一条纸带,电源频率为50 Hz.A、B、C、D、E为在纸带上所选的计数点.相邻计数点间有四个计时点未画出.
(1)小车与纸带________(填“左”或“右”)端连接.
(2)AC段小车的平均速度vAC=________m/s;打下A点时小车的瞬时速度vA=________m/s.
(3)AB、BC、CD、DE间距离分别用x1、x2、x3、x4表示,相邻两计数点时间间隔用T表示,则用x1、x2、x3、x4和T表示小车加速度的表达式a=________;代入数据,求得加速度为a=________m/s2.(计算结果均保留小数点后两位)
解析:(1)小车做匀加速直线运动,计数点之间的距离越来越大,因此小车与纸带的左端相连.
(2)AC段小车平均速度vAC=eq \f(xAC,2T)=eq \f(52.0×10-3,2×5×0.02) m/s=0.26 m/s,vC=eq \f(xBD,2T)=eq \f((84.0-24.0)×10-3,2×5×0.02) m/s=0.30 m/s,vB=eq \f(vA+vC,2),则vA=2vB-vC=2vAC-vC=0.22 m/s.
(3)根据逐差法有a=eq \f((x3+x4)-(x1+x2),4T2),T=5×0.02 s=0.1 s,代入数据得a=0.40 m/s2.
答案:(1)左 (2)0.26 0.22
(3)eq \f((x3+x4)-(x1+x2),4T2) 0.40
常用方法
规律特点
公式法
运用匀变速直线运动的基本公式解题:速度公式vt=v0+at;位移公式s=v0t+eq \f(1,2)at2;位移和速度关系式2as=veq \\al(2,t)-veq \\al(2,0).三个公式都是矢量式,使用时注意各物理量的方向
平均速度法
定义式eq \x\t(v)=eq \f(s,t)对任何直线运动都适用,而eq \x\t(v)=eq \f(1,2)(v0+vt)只适用于匀变速直线运动.恰当地使用平均速度公式,有助于提高解题速度
中间时刻速度法
匀变速直线运动中,任一时间t内中间时刻的瞬时速度等于这段时间内的平均速度,即v中=eq \x\t(v),这一结论适用于任何匀变速直线运动.有些题目应用它可以避免常规解法中用位移公式列出的含有t2的复杂式子,从而简化解题过程,提高解题速度
常用方法
规律特点
巧用推论解题
匀变速直线运动中,在连续相等的时间T内的位移之差为一恒量,即sn+1-sn=aT2,对于一般的匀变速直线运动问题,若出现相等的时间间隔问题,应优先考虑用Δs=aT2求解
比例法
对于初速度为0的匀加速直线运动与末速度为0的匀减速直线运动,可利用初速度为0的匀加速直线运动的推论解题
图像法
应用v-t图像,可把较复杂的物理问题转变为较简单的数学问题,尤其是用图像定性分析,可避开繁杂的计算,快速找出答案
极值法
临界、极值问题的考查往往伴随着“恰好”“刚刚”“最大”“最小”等字眼,极值法在追及等问题中有着广泛的应用
逆向思维法
把运动过程的“末态”作为“初态”反向研究问题的方法,一般用于末态已知的情况
巧选参考系解题
物体的运动是相对一定的参考系而言的,研究地面上的物体的运动常以地面为参考系,有时为了研究问题方便,也可巧妙地选用其他物体作为参考系,甚至在分析某些较为复杂的问题时,为了求解简捷,还可以灵活地选用非惯性参考系
s-t图像
v-t图像
图像
①
表示物体做匀速直线运动,斜率(图线的倾斜程度)表示速度
表示物体做匀加速直线运动,斜率(图线的倾斜程度)表示加速度
②
表示物体静止
表示物体做匀速直线运动
s-t图像
v-t图像
③
表示物体静止
表示物体静止
④
表示物体自s0位置向负方向做匀速直线运动
表示物体以初速度v0向正方向做匀减速直线运动
⑤
交点的横坐标表示三个物体此时刻相遇
交点的横坐标表示三个物体此时刻的速度相等
⑥
t1时刻的位移为s1
t1时刻物体的速度为v1(图中阴影部分的面积表示物体在0~t1时间内的位移)
⑦
与④平行,表示速度相同
与④平行,表示加速度相同
⑧
表示物体做加速直线运动
表示物体做加速度增大的加速运动
s2-s1
s3-s2
s4-s3
s5-s4
s6-s5
Δs平均值
人教版 (2019)必修 第一册第二章 匀变速直线运动的研究综合与测试学案: 这是一份人教版 (2019)必修 第一册第二章 匀变速直线运动的研究综合与测试学案,共10页。
人教版 (2019)必修 第一册第三章 相互作用——力综合与测试导学案: 这是一份人教版 (2019)必修 第一册第三章 相互作用——力综合与测试导学案,共7页。
高中物理人教版 (2019)必修 第一册第四章 运动和力的关系综合与测试导学案: 这是一份高中物理人教版 (2019)必修 第一册第四章 运动和力的关系综合与测试导学案,共5页。