人教版八年级下册17.1 勾股定理优秀课件ppt

这是一份人教版八年级下册17.1 勾股定理优秀课件ppt，共28页。PPT课件主要包含了欣赏下面海螺的图片，素养目标，证明“HL”，解如图所示，即EC的长为3cm，连接中考，解得x3，解如图，∴△ABC即为所求，通常用到方程思想等内容，欢迎下载使用。

在数学中也有这样一幅美丽的“海螺型”图案，如第七届国际数学教育大会的会徽.
2. 能利用勾股定理在数轴上作出表示无理数的点.
1. 会用勾股定理解决简单的实际问题，建立数形结合的思想.
3.灵活运用勾股定理进行计算，并会运用勾股定理解决相应的折叠问题.
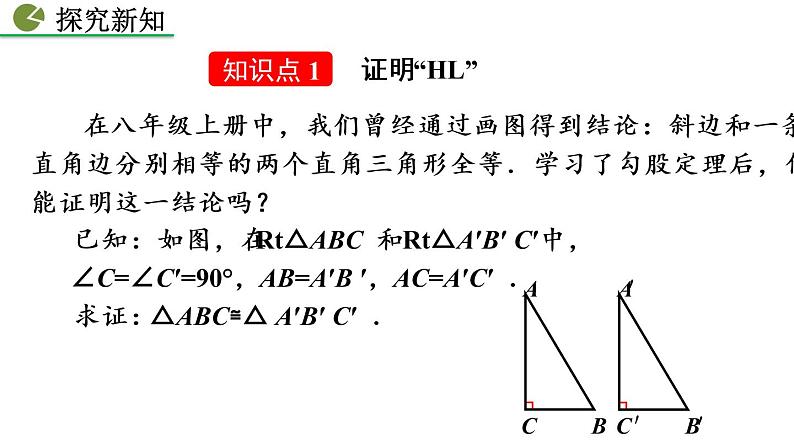
　　在八年级上册中，我们曾经通过画图得到结论：斜边和一条直角边分别相等的两个直角三角形全等．学习了勾股定理后，你能证明这一结论吗？
　　已知：如图，在Rt△ABC 和Rt△A′B′ C′中， ∠C=∠C′=90°，AB=A′B ′，AC=A′C′ ．　　求证：△ABC≌△ A′B′ C′ ．
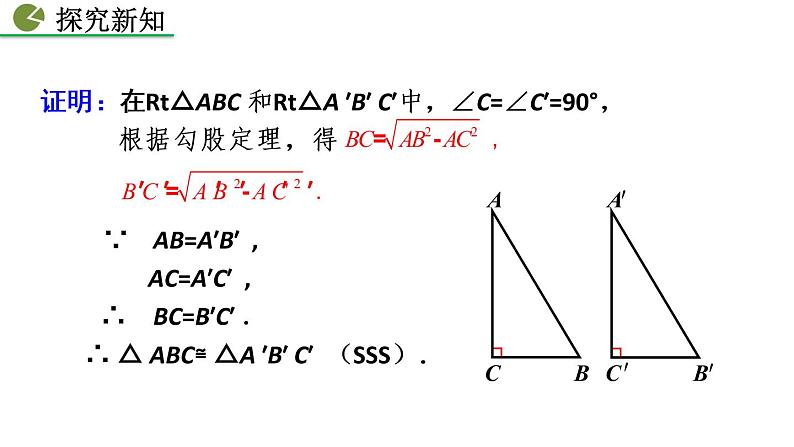
证明：在Rt△ABC 和Rt△A ′B′ C′中，∠C=∠C′=90°， 根据勾股定理，得
∵ AB=A′B′ , AC=A′C′ , ∴　BC=B′C′ ．
∴ △ ABC≌ △A ′B′ C′ （SSS）．
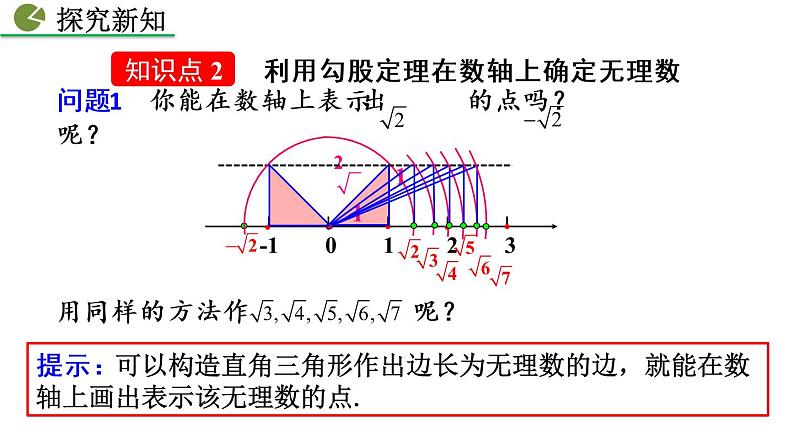
利用勾股定理在数轴上确定无理数
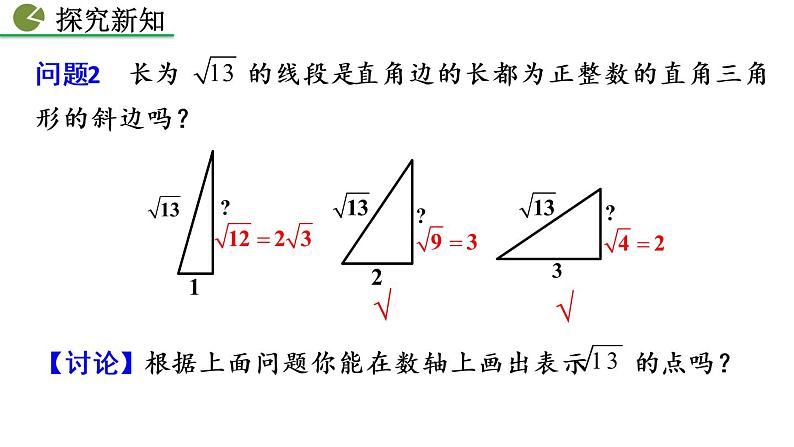
提示：可以构造直角三角形作出边长为无理数的边，就能在数轴上画出表示该无理数的点.
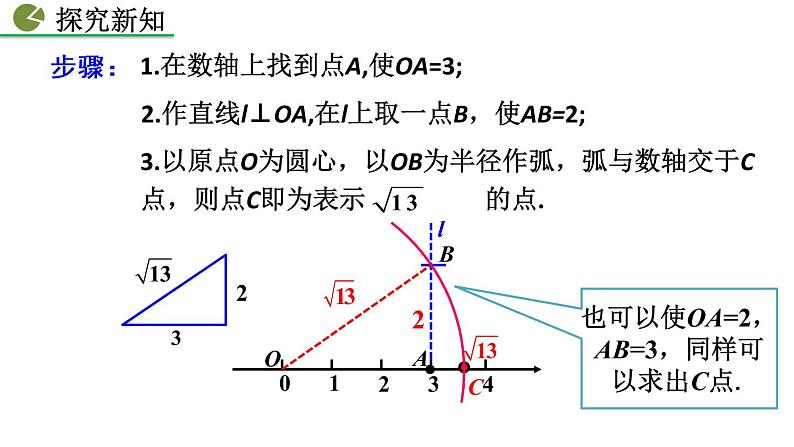
1.在数轴上找到点A,使OA=3;
2.作直线l⊥OA,在l上取一点B，使AB=2;
也可以使OA=2，AB=3，同样可以求出C点.
利用勾股定理表示无理数的方法:
（1）利用勾股定理把一个无理数表示成直角边是两个正数的直角三角形的斜边.
（2）以原点为圆心，以无理数斜边长为半径画弧与数轴存在交点，在原点左边的点表示是负无理数，在原点右边的点表示是正无理数.
例 在数轴上作出表示 的点.
作法：（1）在数轴上找到点A，使OA=1；（2）过点A作直线垂直于OA，在直线上取点B, 使AB=4，那么OB= ；（3）以原点O为圆心，以OB为半径作 弧，弧与数轴交于点C，则OC= . 如图，在数轴上，点C为表示 的点.
如图，点A表示的实数是 （　　）
利用勾股定理在网格上做长度为无理数的线段
小结：勾股定理与网格的综合求线段长时，通常是把线段放在与网格构成的直角三角形中，利用勾股定理求其长度.
解：如图所示，有8条.
如图，四边形ABCD是边长为9的正方形纸片，将其沿MN折叠，使点B落在CD边上的B′处，点A的对应点为A′，且B′C＝3，求AM的长.
解：连接BM，MB′.设AM＝x，在Rt△ABM中，AB2＋AM2＝BM2.在Rt△MDB′中，MD2＋DB′2=MB′2.∵MB＝MB′，∴AB2＋AM2＝MD2＋DB′2，即92＋x2＝(9－x)2＋(9－3)2，解得x＝2.即AM＝2.
利用勾股定理在折叠问题中求线段的长度
折叠问题中结合勾股定理求线段长的方法:(1)设一条未知线段的长为x(一般设所求线段的长为x)；(2)用已知线段或含x的代数式表示出其他线段长；(3)在一个直角三角形中应用勾股定理列出一个关于x的方程；(4)解这个方程，从而求出所求线段长.
如图，折叠长方形ABCD的一边AD，使点D落在BC边的F点处，若AB=8cm，BC=10cm，求EC的长.
解：在Rt△ABF中,由勾股定理得 BF2=AF2－AB2=102－82=36，∴BF=6cm.∴CF=BC－BF=4cm.设EC=xcm，则EF=DE=(8－x)cm ，在Rt△ECF中,根据勾股定理得x2+ 42=(8－x)2，解得 x=3.
如图，在平面直角坐标系中，A（4，0），B（0，3），以点A为圆心，AB长为半径画弧，交x轴的负半轴于点C，则点C坐标为_________．
1.小明学了利用勾股定理在数轴上作一个无理数后，于是在数轴上的2个单位长度的位置找一个点D，然后点D做一条垂直于数轴的线段CD，CD为3个单位长度，以原点为圆心，以到点C的距离为半径作弧，交数轴于一点，则该点位置大致在数轴上（　　）A.2和3之间 B.3和4之间 C.4和5之间 D.5和6之间
2.如图，网格中的小正方形边长均为1，△ABC的三个顶点均在格点上，则AB边上的高为_______.
4.如图，在矩形ABCD中，AB=8，BC=4，将矩形沿AC折叠，点D落在点D′处，求重叠部分△AFC的面积.
解：易证△AFD′≌△CFB(AAS)， ∴D′F=BF，设D′F=x，则AF=8-x，在Rt△AFD′中，AF2=D′F2+AD′2,(8-x)2=x2+42， ∴S△AFC= AF•BC=10．
∴AF=AB-FB=8-3=5，
5.如图，数轴上点A所表示的数为a，求a的值.
解：∵图中的直角三角形的两直角边为1和2，∴斜边长为 ，即-1到A的距离是 ，∴点A所表示的数为 .
提示：求点表示的数时注意画弧的起点不从原点起，因而所表示的数不是斜边长.
利用勾股定理作图或计算
在数轴上表示出无理数的点
利用勾股定理解决网格中的问题
利用勾股定理解决折叠问题及其他图形的计算
通常与网格求线段长或面积结合起来