数学七年级下册9.1.2 不等式的性质一等奖课件ppt

这是一份数学七年级下册9.1.2 不等式的性质一等奖课件ppt，共38页。

等式的基本性质:（1）等式的两边都加上（或都减去）同一个 数或同一个整式，等式仍然成立.（2）等式的两边都乘以（或除以）一个不为0 的数，等式仍然成立.
猜想 ：不等式也具有同样的性质吗？
2. 能够利用不等式的性质解不等式.
1. 掌握不等式的三个性质.
3. 通过实例操作,培养学生观察、分析、比较问题的能力.
等式基本性质1：等式的两边都加上（或减去）同一个整式，等式仍然成立.
如果a=b,那么a±c=b±c.
不等式是否具有类似的性质呢？
那么 7+5 ____ 3+ 5 , 7 -5____3-5
如果-1< 3,那么-1+2____3+2, -1- 4____3 - 4
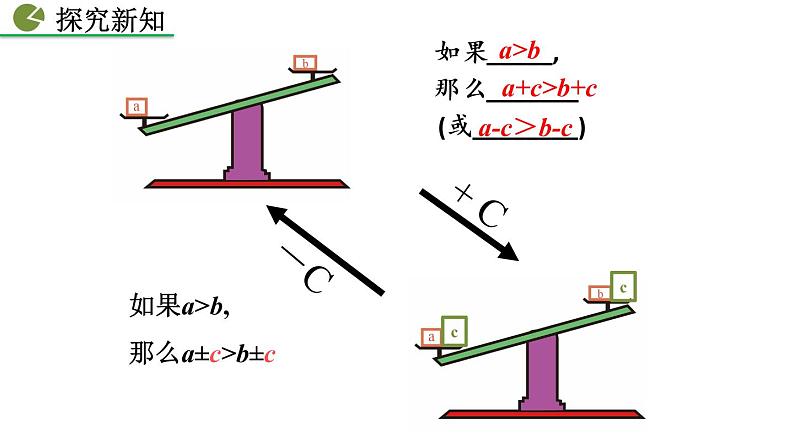
(或________)
如果a>b,那么a±c>b±c
不等式的两边都加上（或减去）同一个整式，不等号的方向不变.
如果____,那么_________.
解：因为 a>b，两边都加上3，
解：因为 a由不等式基本性质1，得
a+3 > b+3；
由不等式基本性质1，得
a-5 < b-5 .
（1）已知 a>b，则a+3 b+3;
（2）已知 a例 用“>”或“<”填空：
利用不等式的性质1解答问题
用“＞”或“＜”填空，并说明是根据不等式的哪一条性质：(1)若x＋3＞6，则x______3，根据______________；(2)若a－2＜3，则a______5，根据____________．
（1）5 3 ；
5×2 3×2 ；
5÷2 3÷2 .
自己再写一个不等式，分别在它的两边都乘（或除以）同一个正数，看看有怎样的结果？与同桌互相交流，你们发现了什么规律？
(或 )
如果_________,
不等式的两边都乘（或除以）同一个正数，不等号的方向不变.
例 设a＞b，用“＜”“＞”填空并回答是根据不等式的哪一条基本性质.
（1） a÷3____b÷3; （2） ; （3） 2a+3____2b+3; （4）(m2+1)a____ (m2+1)b(m为常数).
利用不等式的性质2解答问题
-8÷2___ 4÷2
（1）5 3 ；
5×(-2) 3×（-2） ；
5÷(-2) 3÷(-2) .
自己再写一个不等式，分别在它的两边都乘（或除以）同一个负数，看看有怎样的结果？与同桌互相交流，你们发现了什么规律？
a-a-b>b-a-b
不等式两边同乘以-1，不等号方向改变.
猜想：不等式两边同乘以一个负数，不等号方向改变.
不等式的两边都乘（或除以）同一个负数，不等号的方向改变.
（1）如果a＞b，那么ac＞bc. （2）如果a＞b，那么ac2＞bc2. （3）如果ac2＞bc2，那么a＞b.
你能用不等式的基本性质判断下列说法的正误吗？
√ 因为c≠0，所以c2＞0.
不等式的基本性质与等式的基本性质有什么相同点和不同点？
因为 a>b，两边都乘3，
因为 a>b，两边都乘-1，
由不等式基本性质2，得
由不等式基本性质3，得
（1）已知 a>b，则3a 3b ；
（2）已知 a>b，则-a -b .
例1 用“>”或“<”填空：
利用不等式的性质解答问题
因为 a 由不等式基本性质3，得
由不等式基本性质1，得
（3）已知 a若 a>b, 用“>”或“<”填空： a-5 b-5（根据不等式的性质 ） 6a 6b（根据不等式的性质 ） 2a+4 2b+4 （根据不等式的性质 ） （根据不等式的性质 ）
等式有对称性及传递性，那么不等式具有对称性和传递性吗?
已知x>5,那么5由8如：8<10，10<15 ，8 15.
x>5 5性质4（对称性）:如果a>b,那么b性质5（同向传递性）:如果a>b,b>c,那么a>c.
例2 利用不等式的性质解下列不等式：(1)x-7＞26； (2)3x<2x+1；(3) ；　　 (4)-4x＞3.　　　　
利用不等式的性质解不等式
分析：解未知数为x的不等式，就是要使不等式逐步化为x＞a或x＜a的形式．
解：(1)为了使不等式x-7＞26中不等号的一边变为x，根据不等式的性质1，不等式两边都加7，不等号的方向不变，得 x-7+7 ＞ 26+7， x ＞ 33.
这个不等式的解集在数轴上的表示如图所示：　
（2）为了使不等式3x<2x+1中不等号的一边变为x，根据_____________，不等式两边都减去____，不等号的方向_____，得_________________________
3x-2x＜2x+1-2x， x＜1.
这个不等式的解集在数轴上的表示如图所示：
（3）为了使不等式 中不等号的一边变为x，根据不等式的性质2，不等式的两边都除以　不等号的方向不变，得
这个不等式的解集在数轴上的表示如图所示:
（4）为了使不等式-4x＞3中的不等号的一边变为x，根据______________，不等式两边都除以____，不等号的方向______，得________.
利用不等式的性质解下列不等式:
(2)-2x ＞ 3;
(1)x-5 ＞ -1;
(3)7x ＜ 6x-6.
例3 如果不等式 (a＋1)x＜a＋1可变形为 x＞1，那么a 必须满足________.
解析：根据不等式的基本性质可判断，a＋1为负数，即a＋1＜0，可得 a＜－1.
利用不等式的性质确定字母的值
提示：只有当不等式的两边都乘(或除以)一个负数时，不等号的方向才改变．
a是任意有理数，试比较5a与3a的大小.
这种解法对吗？如果正确，说出它根据的是不等式的哪一条基本性质；如果不正确，请就明理由.
答：这种解法不正确，因为字母a的取值范围我们并不知道.如果 a＜0，那么 5a ＜ 3a ；如果a＝0 ，那么 5a ＝ 3a .
1.如果a＞b，c＜0，那么下列不等式成立的是（　　）A．a+c＞b B．a+c＞b﹣cC．ac﹣1＞bc﹣1 D．a（c﹣1）＜b（c﹣1）
2.不等式5x+1≥3x﹣1的解集在数轴上表示正确的是（　　）A． B．C． D．
1.若x>y，则ax >ay,那么一定有（ ）A.a>0 B. a ≥0 C. a<0 D. a ≤02.与x-2< 0 的解集相同的是 （ ）A. x>1 B. x< 2 C. x<1 D. x ≤ 2
3. 已知a < b，用“>”或“<”填空：
（1）a +12 b +12 ；
（2）b-10 a -10 .
4. 把下列不等式化为x>a或x5.利用不等式的性质解下列不等式,并在数轴上表示．
(2)-2x > 3
(1)x-5 > -1
(3)7x < 6x-6
由不等式3<6 ，李毅和浩轩分别得出的以下两个不等式对吗? (1)李毅：3-a<6-a; (2)浩轩：3a<6a.
解：(1)3<6,根据不等式的性质1得,3-a<6-a;
(2)3<6,当a>0时,根据不等式的性质2得,3a<6a,
当a<0时,根据不等式的性质3得,3a>6a.
已知不等式2a＋3b＞3a＋ 2b,试比较a、b的大小.
解:根据不等式的基本性质1,不等式两边都减去(2a+2b),得2a＋3b－ (2a+2b)＞3a＋ 2b － (2a+2b)2a＋3b－2a － 2b＞3a＋ 2b － 2a － 2b b＞a.
如果a>b，那么a+c>b+c，a-c>b-c