初中数学北师大版七年级上册5.6 应用一元一次方程——追赶小明多媒体教学课件ppt

这是一份初中数学北师大版七年级上册5.6 应用一元一次方程——追赶小明多媒体教学课件ppt，共38页。PPT课件主要包含了追赶问题，对向相遇，练一练，依题意得，解方程得x3，解方程得x2，做一做，乙追上甲时，X3小时，X+1013等内容，欢迎下载使用。

行程问题中的三个基本量及其关系：1．路程＝________×________.2．航行问题中的数量关系： 顺水(风)速度＝静水(风)速度________水流(风)速度； 逆水(风)速度＝静水(风)速度________水流(风)速度．
1.这个问题中的等量关系是什么？2.如何借助“线段图”表示等量关系？
前者走的路程=追者走的路程
线段的总长=各个分段长的和
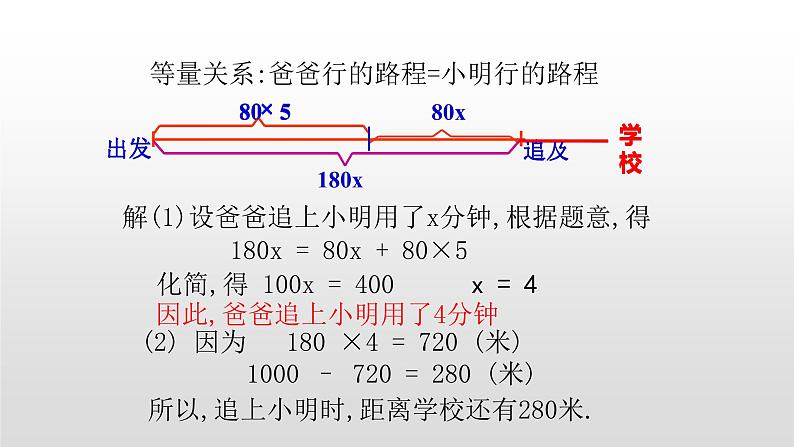
例题:小明同学每天早上要在7：30之前赶到距家1000米的学校上学。一天，小欢以80米/分的速度出发，5分后，小明的爸爸发现他忘了带书包。于是，爸爸立即以180米/分的速度去追小明，并且在途中追上了他。（1）哥哥追上小明用了多长时间？（2）追上小明时，距离学校还有多远？
小明先跑的这段路程是多少呢?
爸爸出发后小明所行的这段路程是多少呢?
哥哥所行的路程是多少呢?
家与学校的距离是1000米小明的速度是80米/分
爸爸的速度是180米/分
小明出发5分钟后哥哥才出发
思考：小明走后面的这段路与爸爸从家里出发到追上小明所用的时间有什么关系？
解(1)设爸爸追上小明用了x分钟,根据题意,得
180x = 80x + 80×5
化简,得 100x = 400
因此,爸爸追上小明用了4分钟
(2) 因为 180 ×4 = 720 (米) 1000 – 720 = 280 (米)
所以,追上小明时,距离学校还有280米.
等量关系:爸爸行的路程=小明行的路程
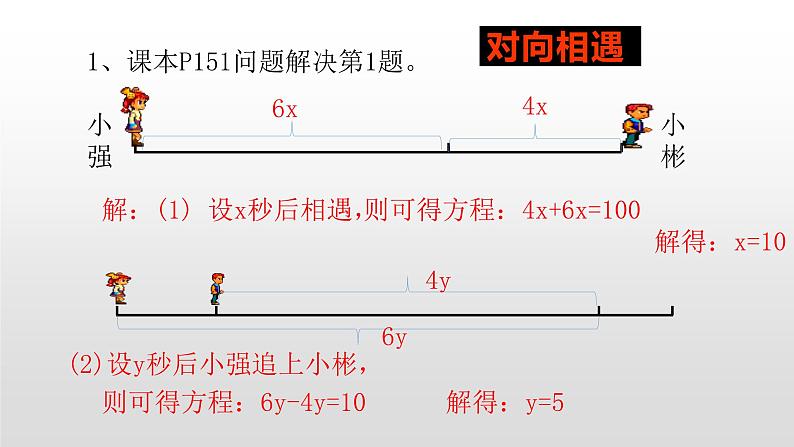
1、课本P151问题解决第1题。
解：(1) 设x秒后相遇，
(2)设y秒后小强追上小彬，
则可得方程：6y-4y=10 解得：y=5
则可得方程：4x+6x=100 解得：x=10
敌我两军相距25km，敌军以5km/h的速度逃跑，我军同时以8km/h的速度追击，并在相距1km处发生战斗，问战斗是在开始追击后几小时发生的？
解：设战斗是在开始追击后x小时发生的. 根据题意，得 8x－5x＝25－1. 解得 x＝8. 答：战斗是在开始追击后8小时发生的.
1、甲乙两地间的路程为450千米，一列慢车从甲站开出，每小时行驶65千米，一列快车从乙站开出，每小时行驶85千米，若两车同时出发，几小时相遇？
设 经过x小时两车相遇,
65x+85x=450
答： 若两车同时出发，3小时相遇。
问题1：后队追上前队用了多长时间 ？
议一议：育红学校七年级学生步行到郊外旅行，1班的学生组成前队，步行的速度为4千米/小时，2班的学生组成后队，速度为6千米/小时，前队出发１小时后，后队出发， 同时后队派一名联络员骑自行车在两队之间不间断地 来回进行联络，他骑车的速度为12千米 /小时。
请根据以上的事实提出问题并尝试回答。
问题2：后队追上前队时联络员行了多少路程？
问题3：联络员第一次追上前队时用了多长时间？
问题4：当后队追上前队时，他们已经行进了多少路程？
问题5：联络员在前队出发多少时间后第一次追上前队？
育红学校七年级学生步行到郊外旅行，1班的学生组成 前队，步行的速度为4千米/小时，2班的学生组成后队， 速度为6千米/小时，前队出发１小时后，后队出发， 同时后队派一名联络员骑自行车在两队之间不间断地 来回进行联络，他骑车的速度为12千米 /小时。
解：设后队追上前队用了x小时，由题意 列方程得：
6x = 4x + 4
答：后队追上前队时用了2小时。
育红学校七年级学生步行到郊外旅行，1班的学生组成 前队，步行的速度为4千米/小时，2班的学生组成后队， 速度为6千米/小时，前队出发１小时后，后队出发， 同时后队派一名联络员骑自行车在两队之间不间断地 来回进行联络，他骑车的速度为12千米 /小时。
解：由问题1得后队追上前队用了2小时，因此 联络员共行进了
12 × 2 = 24 （千米）答：后队追上前队时联络员行了24千米。
解：设联络员第一次追上前队时用了x小时， 由题意列方程得；
12x = 4x + 4
解方程得：x =0.5
答：联络员第一次追上前队时用了0.5小时。
育红学校七年级学生步行到郊外旅行，1班的学生组成前队，步行的速度为4千米/小时，2班的学生组成后队，速度为6千米/小时，前队出发１小时后，后队出发，同时后队派一名联络员骑自行车在两队之间不间断地来回进行联络，他骑车的速度为12千米 /小时。
解：设当后队追上前队时，他们已经行进了x千米， 由题意列方程得：
解得； x = 12答：当后队追上前队时，他们已经行进12千米.
问题5：联络员在前队出发多少时间后第一次追上前队？
解：设联络员在前队出发x小时后第一次追上前队， 由题意列方程得；
答：联络员在前队出发后1.5 小时后第一次追上前队.
4x = 12（x - 1）
解方程得： x = 1.5
解：设经过x小时重新会合
依题意可列方程： 35x+45x=2×10
解方程，得: x=0.25
答：经过0.25小时会合。
完成课本P151“问题解决”第2题
2. 一队学生去校外进行军事训练，他们以每小时5千米的速度行进，走了18分钟，学校要将一个紧急通知传给队长，通讯员从学校出发，骑自行车以每小时14千米的速度按原路追上去，通讯员需要多长时间可以追上学生队伍？
甲步行上午7时从A地出发，于下午5时到达B地，乙骑自行车上午10时从A地出发，于下午3时到达B地，问乙在什么时间追上甲的？
分析:设A，B两地间的距离为1，根据题意得:甲步行走全程需要10小时，则甲的速度为_______. 乙骑车走全程需要5小时，则乙的速度为_______.
等量关系: 1、甲的用时=乙的用时+3小时 2、甲走的路程=乙走的路程.
略解，设乙用了X小时： (X+3)= X
解：72 km/h＝20 m/s，设听到回声时，汽车离山谷x m.由题意，得2x＋4×20＝340×4，解得x＝640.答：听到回声时，汽车离山谷640 m.
1．汽车以72 km/h的速度在公路上行驶，开向寂静的山谷，驾驶员摁一下喇叭，4 s后听到回声，已知空气中声音的传播速度约为340 m/s，这时汽车离山谷多远？
2．一个车队共有n(n为正整数)辆小轿车，正以36 km/h的速度在一条笔直的街道上匀速行驶，行驶时车与车的间隔均为5.4 m，甲停在路边等人，他发现该车队从第一辆车的车头到最后一辆车的车尾经过自己身边共用了20 s的时间，假设每辆车的车长均为4.87 m.(1)求n的值；
36 km/h＝10 m/s，则4.87n＋5.4(n－1)＝20×10，解得n＝20.
(2)一个车队共有n(n为正整数)辆小轿车，正以36 km/h的速度在一条笔直的街道上匀速行驶，行驶时车与车的间隔均为5.4 m，若乙在街道一侧的人行道上与车队同向而行，速度为v m/s，当车队的第一辆车的车头从他身边经过了15 s时，为了躲避一只小狗，他突然以3v m/s的速度向前跑，这样从第一辆车的车头到最后一辆车的车尾经过他身边共用了35 s，求v的值．
车队的总长度为20×4.87＋5.4×19＝200(m)．由题意，得(10－v)×15＋(10－3v)×(35－15)＝200.解得v＝2.
3．一架飞机在A，B两城市之间飞行，风速为20 km/h，顺风飞行需要8 h，逆风飞行需要8.5 h．求无风时飞机的飞行速度和A，B两城市之间的航程．
解：设无风时飞机的飞行速度为x km/h.根据题意，得8(x＋20)＝8.5(x－20)，解得x＝660.
物体在风中或水中行。顺速为物体速度与水中速度二速度之和，逆速为二速度之差。
顺风：无风时飞机的飞行速度+风速=飞机实际速度
所以8(x＋20)＝8×(660＋20)＝5 440.答：无风时飞机的飞行速度为660 km/h，A，B两城市之间的航程为5 440 km.
4．一条笔直的河流上有甲、乙两艘船，现同时由A地顺流而下，乙船到B地时接到通知，须立即逆流而上返回C地执行任务，甲船继续顺流航行．已知甲、乙两船在静水中的速度都是7.5 km/h，水流速度为2.5 km/h，A，C两地间的距离为10 km.如果乙船由A地经B地再到达C地共用了4 h，问：乙船到达C地时，甲船距离B地有多远？
顺流：静水中的速度+水流速度=船的实际速度
设乙船由B地航行到C地用了x h，那么甲、乙两船由A地到B地都用了(4－x) h，A地到B地的距离是(7.5＋2.5)(4－x) km，B地到C地的距离是(7.5－2.5)x km.①若C地在A，B两地之间，根据A地到B地的距离－B地到C地的距离＝A，C两地间的距离，得(7.5＋2.5)(4－x)－(7.5－2.5)x＝10.整理，得10(4－x)－5x＝10.
去括号，得40－10x－5x＝10.移项、合并同类项，得－15x＝－30.系数化为1，得x＝2.所以甲船距离B地有(7.5＋2.5)×2＝20(km)远．②若C地不在A，B两地之间，根据B地到C地的距离－A地到B地的距离＝A，C两地间的距离，得(7.5－2.5)x－(7.5＋2.5)(4－x)＝10.
问题1：操场一周是400米，小花每秒跑5米,小明每秒9米,两人绕跑道同时同地同向而行，他俩能相遇吗？
1、所用时间相同2、小明跑的路=小花跑的路程+400（跑道周长）
解：设经过x秒两人第一次相遇，依题意，得
10x-5x=400,
答：经过80秒两人第一次相遇
变式训练：操场一周是400米，小明每秒跑5米,小华骑自行车每秒10米,两人绕跑道同时同地同向而行，两人同时同地相背而行，则两个人何时相遇？
10x+5x=400,
1、所用时间相同2、小明跑的路+小花跑的路程=400
1．行程问题中常用的数量关系基本关系：路程＝________________．相遇问题：甲、乙相向而行，则甲走的路程＋乙走的路程＝_______________．追及问题：甲、乙同向不同地，则后者走的路程＝前者走的路程＋____________________．
时间，路程，速度是否具有等量关系
2．环形跑道问题数量关系：(1)甲、乙两人在环形跑道上同时同地同向出发，则快的必须多跑一圈才能追上慢的；(2)甲、乙两人在环形跑道上同时同地反向出发，则两人首次相遇时所走的路程之和等于环形跑道一圈的长度．3．航行问题数量关系：(1)顺水速度＝____________＋________；(2)逆水速度＝____________－________；(3)顺水速度－____________＝2×________．
3.甲、乙二人在环形跑道上同时同地出发，同向运动，若甲的速度是乙的速度的2倍，则甲运动2周，甲、乙第一次相遇，若甲的速度是乙的速度的3倍，则甲运动2(3)周，甲、乙第一次相遇；若甲的速度是乙的速度的4倍，则甲运动3(4)周，甲、乙第一次相遇，…，以此探究正常走时的时钟，时针和分针从0点（12点）同时出发，分针旋转　　　　　周，时针和分针第一次相遇.